对称加密和非对称加密

上一篇文章中我们写了https的安全性，里面涉及到对称加密和非对称加密等。

这一章节我们就来简单了解一下：

 

1、对称加密算法：

加密和解密用到的密钥是相同的，这种加密方式加密速度非常快，适合经常发送数据的场合。缺点是密钥的传输比较麻烦。如AES算法；

2、非对称加密算法：

加密和解密用的密钥是不同的，这种加密方式是用数学上的难解问题构造的，通常加密解密的速度比较慢，适合偶尔发送数据的场合。优点是密钥传输方便。常见的非对称加密算法为RSA、ECC和EIGamal。

非对称加密算法的加密模式：

（1）乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。

（2）甲方获取乙方的公钥，然后用它对信息加密。

（3）乙方得到加密后的信息，用私钥解密。

 

 

3、AES加密算法：

高级加密标准(AES,Advanced Encryption Standard)为最常见的对称加密算法(微信小程序加密传输就是用这个加密算法的)。

对称加密算法也就是加密和解密用相同的密钥，具体的加密流程如下图：

 

 

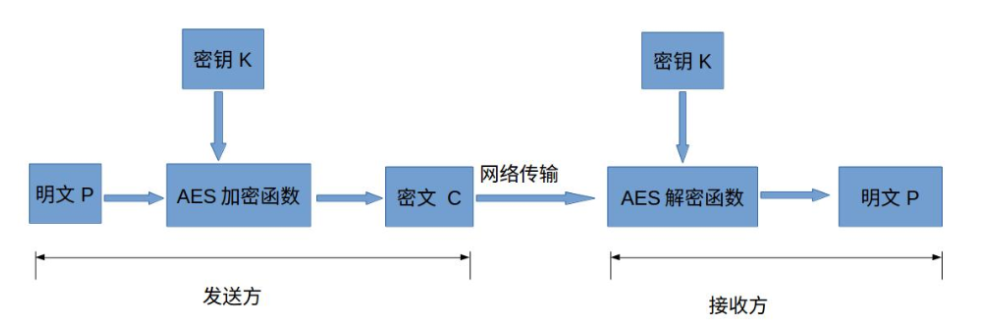
 注释：

• 明文P：没有经过加密的数据。
• 秘钥K：用来加密明文的密码，在对称加密算法中，加密与解密的密钥是相同的。密钥为接收方与发送方协商产生，但不可以直接在网络上传输，否则会导致密钥泄漏，通常是通过非对称加密算法加密密钥，然后再通过网络传输给对方，或者直接面对面商量密钥。密钥是绝对不可以泄漏的，否则会被攻击者还原密文，窃取机密数据。
• AES加密函数：设加密函数为E，密文为C，则C=E(K, P)；
• 密文C：加密后的数据；
• AES解密函数：设解密函数为D，则P=D(K, C)；

 

4、RSA算法

强烈推荐看阮老师的博客讲解：RSA算法原理（二）

文章深入浅出，通俗易懂。并且举了一个小李子。

我在这里摘录部分如下：

假设Bob要与Alice进行加密通信，在这里Bob可以看做是客户端，Alice可以看做是服务器。那么我们知道服务器自己要生成私钥和公钥，那么它是如何生成的呢？

 

 

 秘钥生成步骤：（虽然看不懂，但还是要学习嘛）

第一步，Alice（服务器）随机选择两个不相等的质数p和q。

第二步，计算p和q的乘积n。

第三步，计算n的欧拉函数φ(n)。

第四步，随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。

第五步，计算e对于φ(n)的模反元素d。

第六步，将n和e封装成公钥，n和d封装成私钥。

 

在这个Bob与Alice的通信例子中，我们假设n=3233，e=17，d=2753，

那么公钥就是 (3233,17)，私钥就是（3233, 2753）；

实际应用中，公钥和私钥的数据都采用ASN.1格式表达。

 

4.1、RSA的可靠性

回顾上面的密钥生成步骤，一共出现六个数字：

   p，q，n，φ(n)，e，d 

这六个数字之中，公钥用到了两个（n和e），其余四个数字都是不公开的。

其中最关键的是d，因为n和d组成了私钥，一旦d泄漏，就等于私钥泄漏。

推论步骤我在这里就不说了，我只放结论：如果n可以被因数分解，d就可以算出，也就意味着私钥被破解。

wiki百科这样说：

"对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。

假如有人找到一种快速因数分解的算法，那么RSA的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA密钥才可能被暴力破解。到2008年为止，世界上还没有任何可靠的攻击RSA算法的方式。

只要密钥长度足够长，用RSA加密的信息实际上是不能被解破的。"

4.2、加密和解密

加密要用公钥 (n,e)

假设鲍勃要向爱丽丝发送加密信息m，他就要用爱丽丝的公钥 (n,e) 对m进行加密；

解密要用私钥(n,d)

爱丽丝拿到鲍勃发来的密文以后，就用自己的私钥(n, d) 进行解密；

我们可以看到，如果不知道d，就没有办法从c求出m。而前面已经说过，要知道d就必须分解n，这是极难做到的，所以RSA算法保证了通信安全。

 

 

 RSA三位大佬镇楼（Rivest、Shamir 和 Adleman）

 

 

 

 

Over.......