算法图解—最小覆盖子串

【题目描述】

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

示例 2：

输入：s = "a", t = "a"
输出："a"

示例 3：

输入：s = "a", t = "bb"
输出：""

来源：力扣（LeetCode）第76题
链接：https://leetcode-cn.com/problems/minimum-window-substring
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

熟悉的童靴都知道，这道题属于双指针的经典题目：

我们称之为“滑动窗口”。

【题目分析】

我们先看看题目是什么意思。

本问题要求我们返回字符串 s中包含字符串 t 的全部字符的最小窗口。

我们称包含 t 的全部字母的窗口为「可行」窗口。

通过示例很容易明白题目意思，只要窗口里包含有目标字符串t中的左右字符，且要求是最短的。

那么什么是“滑动窗口”呢？

我把它比作家中的铝合金推拉窗。

 

 

 对就是上图的这个东东。

在滑动窗口类型的问题中都会有两个指针。一个用于「延伸」现有窗口的 right 指针（右侧），和一个用于「收缩」窗口的 left 指针（左侧）。在任意时刻，只有一个指针运动，而另一个保持静止。我们在 s 上滑动窗口，通过移动 right 指针不断扩张窗口。当窗口包含 t 中全部所需的字符后，如果左侧能收缩，我们就收缩窗口（左侧指针  left）直到得到最小窗口。

有人会问，为什么收缩要从左侧指针方向？

因为，你扩张是从右侧的，当停止扩张时，你想想，为什么会停止扩张？是因为当窗口包含 t 中全部所需的字符了。所有此时最右侧的字符一定是必须的，故要从左侧缩减，如果能的话。

 

【图解示例：参考leetCode】

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/minimum-window-substring/solution/zui-xiao-fu-gai-zi-chuan-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

假设：

s  = ABAACBAB
t  =  ABC

第一步：

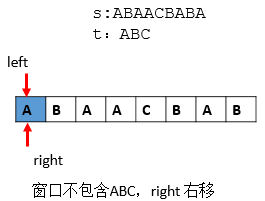
第二步：从第一步到第四步中间少了四步即是从A->B->A->A

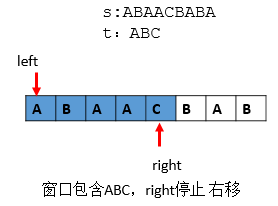
第三步：left 缩减至B，仍然是包含了ABC，但不知道是否是最短，只好记录下来left ，right，len = right - left。

第四步：继续缩减；

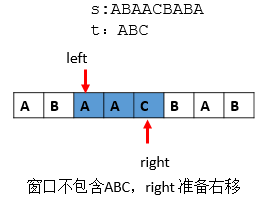
第五步：再次包含ABC，记录下此时的left ，right，len = len>(right - left) ? (right - left) ： len。

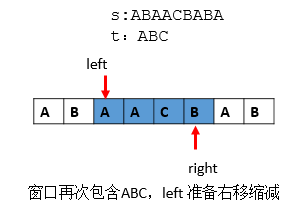
第六步：仍然包含ABC，记录下此时的left ，right，len = len>(right - left) ? (right - left) ： len。left 继续右移。

 

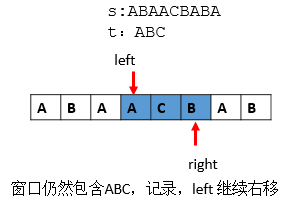
第七步：

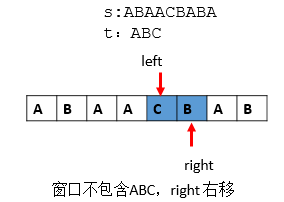
第八步：同上，记录，比较。不在赘述。

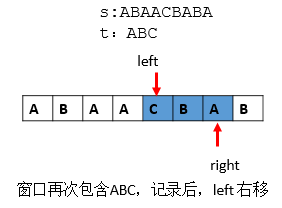
第九步：

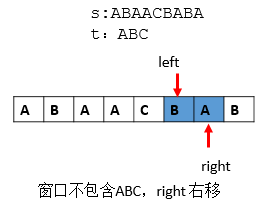
第十步：至此后，结束。

 

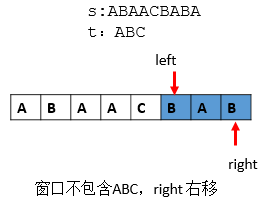
 思路知道了，那么说一说细节：

1、如何判断当前的窗口包含所有 t 所需的字符呢？

这涉及到数据结构的运用了，我们知道Java中hashMap查找的时间复杂度是O(1)。

借此，我们可以用一个需要匹配的哈希表 need<char, int> 表示 t 中所有的字符以及它们的个数，用一个窗口匹配哈希表 windows<char, int> 动态维护窗口中所有的字符以及它们的个数，如果这个动态表中包含 t 的哈希表中的所有字符，并且对应的个数都不小于 t 的哈希表中各个字符的个数，那么当前的窗口是「可行」的，即是满足“包含”的条件的。

2、如何判断这个动态表windows中是否包含 t 的哈希表中的所有字符，并且对应的个数都不小于 t 的哈希表中各个字符的个数？

可以利用一个int 变量即可，设为kind，我称之为种类，即当windows中达到need中某字符的数量时，该变量加1。

【代码实现】

//C++
class Solution {
public:
    string minWindow(string s, string t) {
        //if(s.size() < t.size()) return "";
        unordered_map<char, int> need,windows;
        for(char c:t) need[c]++;
        int kind = 0;//windows中的种类
        int left = 0;
        int right = 0;
        int len = INT_MAX;//返回长度
        int start = 0;//返回起始下标
        while(right < s.size()){
            //current char
            char c = s[right++];
            if(need.count(c)){
                windows[c]++;
                if(windows[c] == need[c]){
                    kind++;
                }
            }
            //if windows中种类齐全了，缩减左侧
            while(kind == need.size()){
                
                if(right - left < len){
                    start = left;
                    len = right - left;
                }
                char d = s[left++];
                if(need.count(d)){
                    windows[d]--;
                    if(need[d] > windows[d]){
                        kind--;
                    }
                }
            }
        }
        return len == INT_MAX ? "" : s.substr(start,len);
    }
};

【Java】

class Solution {
    Map<Character, Integer> ori = new HashMap<Character, Integer>();
    Map<Character, Integer> cnt = new HashMap<Character, Integer>();

    public String minWindow(String s, String t) {
        int tLen = t.length();
        for (int i = 0; i < tLen; i++) {
            char c = t.charAt(i);
            ori.put(c, ori.getOrDefault(c, 0) + 1);
        }
        int l = 0, r = -1;
        int len = Integer.MAX_VALUE, ansL = -1, ansR = -1;
        int sLen = s.length();
        while (r < sLen) {
            ++r;
            if (r < sLen && ori.containsKey(s.charAt(r))) {
                cnt.put(s.charAt(r), cnt.getOrDefault(s.charAt(r), 0) + 1);
            }
            while (check() && l <= r) {
                if (r - l + 1 < len) {
                    len = r - l + 1;
                    ansL = l;
                    ansR = l + len;
                }
                if (ori.containsKey(s.charAt(l))) {
                    cnt.put(s.charAt(l), cnt.getOrDefault(s.charAt(l), 0) - 1);
                }
                ++l;
            }
        }
        return ansL == -1 ? "" : s.substring(ansL, ansR);
    }

    public boolean check() {
        Iterator iter = ori.entrySet().iterator(); 
        while (iter.hasNext()) { 
            Map.Entry entry = (Map.Entry) iter.next(); 
            Character key = (Character) entry.getKey(); 
            Integer val = (Integer) entry.getValue(); 
            if (cnt.getOrDefault(key, 0) < val) {
                return false;
            }
        } 
        return true;
    }
}

 

【复杂度分析】

• 时间复杂度：最坏情况下左右指针对 s 的每个元素各遍历一遍，哈希表中对 s 中的每个元素各插入、删除一次，对 t 中的元素各插入一次。每次检查是否可行会遍历整个 t 的哈希表，哈希表的大小与字符集的大小有关，设字符集大小为 C，则渐进时间复杂度为 O(C⋅∣s∣+∣t∣)。
• 空间复杂度：这里用了两张哈希表作为辅助空间，每张哈希表最多不会存放超过字符集大小的键值对，我们设字符集大小为 C ，则渐进空间复杂度为 O(C)。

 

 

 

Over...