图解算法——恢复一棵二叉搜索树(BST)
题目来源
基础:给你二叉搜索树的根节点 root ,该树中的两个节点被错误地交换。请在不改变其结构的情况下,恢复这棵树。
进阶:使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用常数空间的解决方案吗?
示例1:
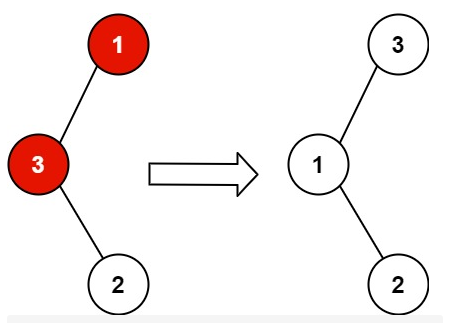
输入:root = [1,3,null,null,2] 输出:[3,1,null,null,2] 解释:3 不能是 1 左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例2:

输入:root = [3,1,4,null,null,2] 输出:[2,1,4,null,null,3] 解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/recover-binary-search-tree 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目解析
什么意思呢?这是其实是两道题,第一道是基础的,就是用基本的解法即可,关键是第二种如何优化你的算法。
好,我们先说第一种,大众思维。
既然题目上说了错误地交换了搜索二叉树(BST)的两个节点,那么BST又有什么特点呢?
我们知道中序遍历搜索BST会得到一组升序的数组(比如:[1,2,3,4,5,6,7,8]),那好,按照题意我们交换两组节点2和6,数组变成[1,6,3,4,5,2,7,8],此时 可发现数组的升序被打破了,因为6>3,5>2。没错,我们就利用该性质是不是就可以找出交换的两个节点位置,然后做交换就好了?
解析方法归纳:
1、先得到BST中序遍历的数组序列;
2、找到不满足条件的位置;
3、看节点数有几个:
3.1、如果有两个,即[1,6,3,4,5,2,7,8]中6>3,5>2,那么就将位置分别记为 i 和 j(i < j,其中i是6,j是5,特别提醒并不是2哦),对应的交换错的节点为 Ai 和 Aj+1 (Ai > Ai+1 && Aj > Aj+1),我们分别记为x,y;
3.2、如果有一个,即[1,2,3,5,4,6,7,8]中的5>4,那么就将位置记为 i ,交换错的位置就是Ai 和 Ai+1,我们分别记为x,y;
4、遍历树,交换节点 x , y 。
好了。思路也很清楚了,关键是如何实现。
第一步:先序遍历BST这应该挺简单的,递归嘛,我们将数组定位为nums来记录:
//c++
第二步:找到不满足条件的位置;但是该位置可能有一个,也可能有两个,所以,得要遍历数组一次。
vector<int> find2val(TreeNode* root, vector<int>& nums){ int n1 = 0; int n2 = 0; bool sec = false; for(int i = 0; i<nums.size()-1; i++){ if(nums[i]>nums[i+1]){ if(!sec){ n1 = nums[i]; n2 = nums[i+1]; sec = true; } else n2 = nums[i+1]; } } return {n1,n2}; }
第三步:看数组中到底有几次
我们这里在主函数中直接就写成2了,因为最多为两次,当然也可以将这个次数记录下来;
第四步:遍历树,换位置
void reverse(TreeNode * root, int count, int x, int y){ if(root!=nullptr){ if(root->val == x || root->val == y){ root->val = (root->val == x) ? y : x;//swap (x,y) if(--count == 0){//来计数是第几次如果是第二次了后面的就不用再遍历了; return; } } reverse(root->left,count,x,y); reverse(root->right,count,x,y); } }
第五步:主函数
void recoverTree(TreeNode* root) { vector<int> nums; inOrder(root, nums);//第一步中序遍历得到升序数组 vector<int> swap_vals = find2val(root, nums);//找到两个被错误交换的值 reverse(root,2,swap_vals[0],swap_vals[1]);//遍历树,进行交换; }
算法分析:
- 时间复杂度:O(N),其中N为BST的节点数。中序遍历要O(N)的时间,而判断交换节点在哪里,最好的情况是O(1),最坏的情况是O(N),所以是O(N);
- 空间复杂度:O(N),因为用到了一个数组来存放升序数列;
以上是一般大众思维,那么如何进行优化呢?优化的点在哪里呢?
其实,我们没有必要去引入这个nums数组,因为我们在中序遍历树时,如果去维护一个前节点变量,那么我们就可以在遍历过程中直接进行比较,我们在这里引入一个栈,并且迭代实现中序遍历,并不是递归。具体用法看下面;
如:
3 / \ 1 4 / 2
第一步:中序遍历,先找到最左节点,中途所有的节点都入栈;

第二步:继续;

第三步:取栈顶元素,并赋予前一个节点变量pred,并向弹出的节点的右子树走;
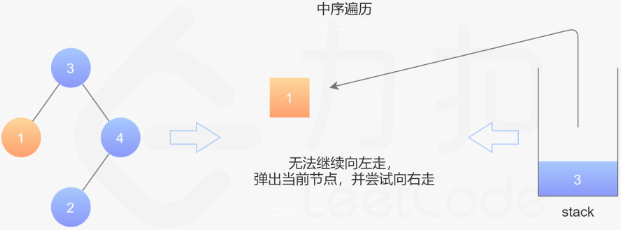
第四步:继续,因为1的右节点,也是NULL,故继续弹栈,弹出来也就是1的父节点3;赋予前一个节点变量pred=3;
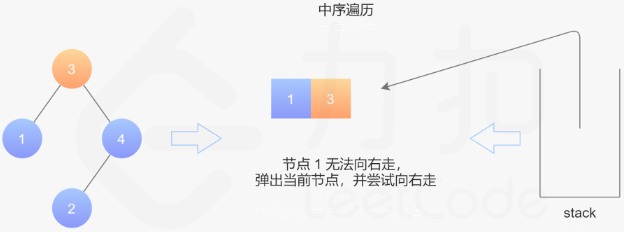
第五步:遍历右子树,有值,寻找右子树中的最左节点,并将沿途所遍历的节点都入栈;
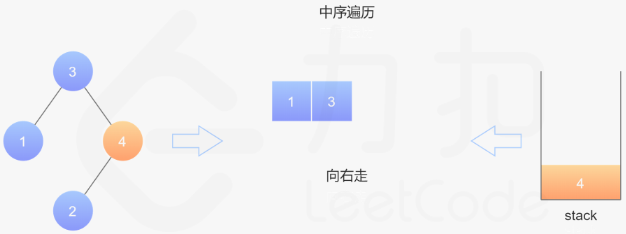
第六步:入栈,找到右子树的最左节点;

第七步:弹出栈顶,此时相当于,找到了以 3 为根节点的,中序遍历中左子树的最后一个节点值,和右子树中的第一个值。这句话的意思是,当你中序遍历时,3的前后值分别为 1 和 2 ;
看好这里,发现了前后节点值大小异常:2 < 3,记录下这两个节点Node1,Node2;

第八步:继续;
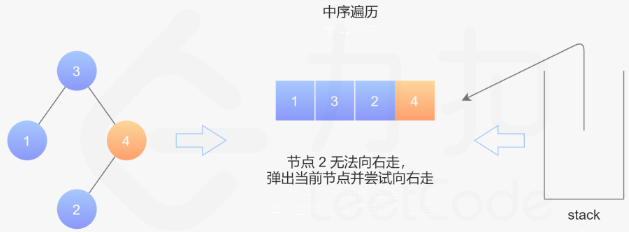
第九步:遍历完毕,找到了交换的点Node1,Node2,进行交换即可;

代码实现:
class Solution { public: void recoverTree(TreeNode* root) { stack<TreeNode*> stk; TreeNode* x = nullptr; TreeNode* y = nullptr; TreeNode* pred = nullptr; while (!stk.empty() || root != nullptr) { while (root != nullptr) { stk.push(root); root = root->left; } root = stk.top(); stk.pop(); if (pred != nullptr && root->val < pred->val) { y = root; if (x == nullptr) { x = pred; } else break; } pred = root; root = root->right; } swap(x->val, y->val); } };
这部分图来自:
作者:LeetCode-Solution 链接:https://leetcode-cn.com/problems/recover-binary-search-tree/solution/hui-fu-er-cha-sou-suo-shu-by-leetcode-solution/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
复杂度分析:
- 时间复杂度:最坏情况下是需要遍历整棵树(即交换节点为BST的最右侧的两个节点),时间复杂度为O(N),N为节点个数;
- 空间复杂度:O(H),H为BST的高度;注意:中序遍历的时候,栈的深度取决于树的高度噢!!!
亲爱的,你们以为到这里就结束了吗?
错,大错特错,在这里突然冒出一个Morris中序遍历算法,这个算法之前是真的不知道。无知了...



