图解算法——KMP算法

KMP算法

 

解决的是包,含问题。

Str1中是否包含str2，如果包含，则返回子串开始位置。否则返回-1。

示例1：

Str1:abcd123def     

Str2:123d

 

暴力法：

从str1的第一个字二哥符开始依此匹配，当以第一个字符开头的子串匹配不上时，开始从第二个字符开始。缺点：每一次匹配都是互相独立的。

复杂度为O(N*M)，且N>=M。因为N<M就肯定不包含M长度的子串。

 

 

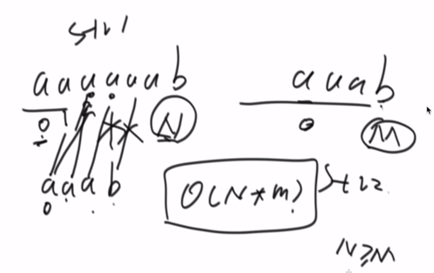
KMP算法将每一次的匹配进行了交涉。

此时，加入了字符串前后缀的概念。但要保证前后缀不能等于该字符串的长度。

以下分别以abcabcd和aaaaab字符串为例。

假设有这样的函数可以实现str2中每个位置的前面子串的最长前后缀。那么，

KMP算法的步骤就是：由原来的str1的i+1和str2的0匹配，改变为由str1的j和str2的0匹配，即由str1的x和str2的z匹配。如下图示：

举例说明：

 

 

 

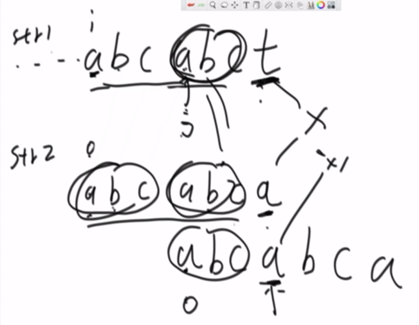
 过程图解：

 

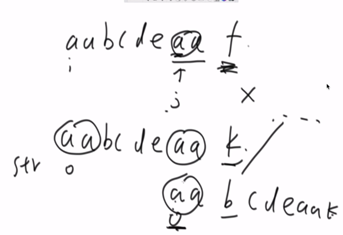
 加速实质解析:  否定了从str1中的i+1位置到j-1位置能配出str2的可能性。

进一步解析：

假设从str1中的i+1位置到j-1位置中有一个k位置开始匹配能配出str2。

那么就会存在在str1的k位置开始有一个后缀串和str2的前缀串相等。但是这又是和最长前后串的概念相违背的。故不成立。

再举一个把str2两次后推的例子（一次匹配不成功）：

 

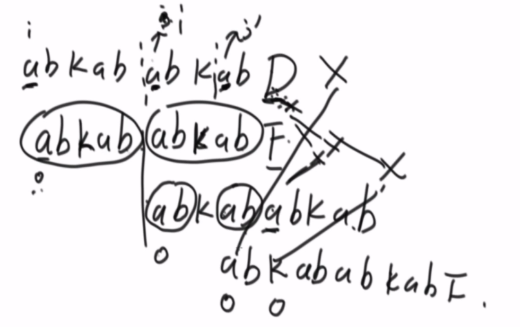
 抽象出来就是：第一次匹配从str1的i开始和str2的0位置开始，匹配到最后到了甲指向的x位置和乙指向的Y位置，发现不匹配。则乙指向Y所对应的最长前后缀长度，即str2中位置指针乙回退到图示位置。下一步继续乙和甲（X）的下一个位置进行比较，这是为什么呢？因为两个画圈圈的部分是相等的，因为最长前后缀原理。

 

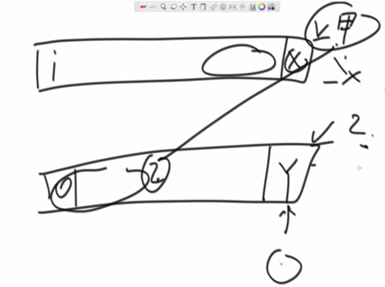
 然后就是求解如何求得str2每个位置上的元素所对应的前面子串的最长前后缀位置。

原理如图：在0位置上设定为-1，1位置上设定为0，2位置上当0和1位置上相同时设定为1，否则设定为0。

 

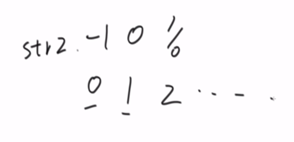
 然后利用数学归纳法：求i位置上的索引长度。假设i-1位置上索引长度是4，则看位置为4的下一位，也就是位置为5的位置上（前缀的下一个字符）和i-1位置上的字符是否相等，如果相等，则i位置上的索引长度就是i位置上索引长度+1，即4+1=5。

 

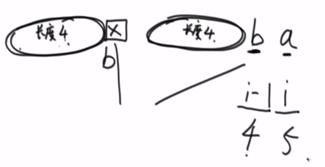
 再举一例：

 

 如果i-1位置上的索引长度4所对应的位置上的元素c和i-1位置上的元素t是否相等，如果相等，则i位置上的元素k所对应的索引长度就是i-1位置上的索引长度+1,即是5。如果不相等，则比较i-1位置上的索引长度4所对应的位置上的元素c的索引长度对应的元素a和i-1位置上的元素t是否相等，如果相等，则i位置上的元素k所对应的索引长度就是元素a所在位置上的索引长度+1,即是1+1=2，否则继续比较直至到该位置上对应的索引长度为0或者-1。类似于递归，也是数学归纳，不断往前看，往前寻找。

 

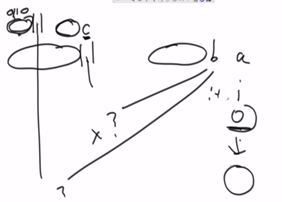
 示例：

左侧是第一次比较c与t，第二次比较a与t都不对，a处已经对应的索引长度为0了，不能再继续向上寻找了，故i位置的k所对应的索引长度为0。

右图是第一次比较c与a，第二次比较a与a，匹配对了，此时c处对应的索引长度为2(ab)，故i位置的k所对应的索引长度为2+1=3。

 

 

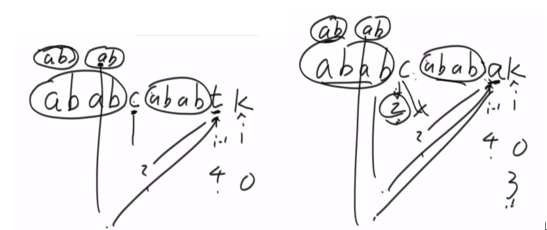
需要注意的是，永远和i-1位置上的元素去比较。直到比较相等，不相等就往前跳继续比较，直至到0。

代码如下：

public class KMPtest {
    public static int getIndexOf(String s,String m) {
        if (s==null || m==null || m.length()<1 || s.length()<m.length()) {
            return -1;
        }
        char[] str1 = s.toCharArray();
        char[] str2 = m.toCharArray();
        int i1 = 0;
        int i2 = 0;
        //str2的以i为结尾的最长回文子串
        int[] next = getNextArray(str2);
        
        while(i1<str1.length && i2<str2.length) {
            if(str1[i1] == str2[i2]) {
                i1++;
                i2++;
            }else if (next[i2] == -1) {
                //说明str2指针回到了头部
                i1++;
            }else {
                //说明str2指针还没到头部，存在回文数组
                i2 = next[i2];
            }
        }
        
        return i2==str2.length ? (i1-i2) : -1;
    }

    private static int[] getNextArray(char[] str2) {
        if(str2.length == 1) {
            return new int[] {-1};
        }
        int[] next = new int[str2.length];
        next[0] = -1;
        next[1] = 0;
        int index = 2;
        int cn = 0;//即将向前跳到的下标
        while(index<next.length) {
            if (str2[index - 1] == str2[cn]) {
                next[index++] = ++cn;
            }else if (cn > 0) {//还能往前跳
                cn = next[cn];
            }else {
                next[index++] = 0;
            }
        }
        return next;
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        System.out.println("sub String index:"+getIndexOf("ababcababak","ababa"));
    }

}

输出结果为：

sub String index:5

 

 

 

实战题目：

题目：

树的包含。

就是在左树T1是否包含右树T2。

思路：将树序列化成字符串（字符数组），要把NULL也加入，否则单纯先序中序是不行的。然后利用KMP算法。

 

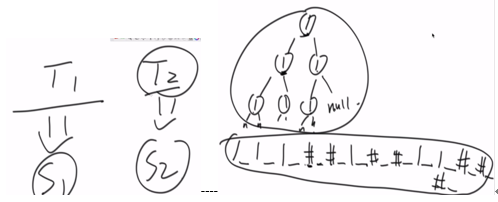
 加入NULL的意义：

 

 

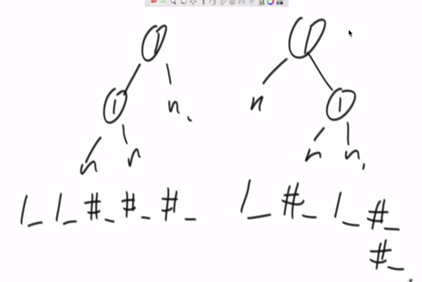
二题：

看一个串是否是范式得到的，如：abcabcabcabc，即是abc*n得到的。

该思路就是看每个字符的索引长度值是否是倍数关系。

 

 

 

Over......