动漫算法梳理

【写在前言】

最近关注了好几个好友专门讲算法的公主号，赶脚还不错，本着“分享”、“共进”的初心，在征得本人的同意之下，特此将原内容经原作者本人同意授权后，重新编辑、排版、整理到此处。

在此，特别感谢小夕学算法，袁厨的算法小屋等原创作者大牛。

好了，话不多说，我要开启学习，和大家共同进步了，嘻嘻~~~

 

【正文开始】

本文摘自【小夕】，点击可看原文

 

题目：

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为[1,2,3,4,5]的一个旋转，该数组的最小值为1。

示例1：
输入：[3,4,5,1,2]
输出：1

示例2：
输入：[2,2,2,0,1]
输出：0

来源：力扣（LeetCode）、剑指offer11
链接：https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof

 

有人说，像我下面这样一个循环不就A了吗？而且击败率100%，还有什么知识点？

如果你也这样想，那就大错特错了。且听我慢慢道来~~~

 

 

 

那么疑问来了，为什么这样写不是最优的呢？

因为这就涉及到了复杂度的问题，一般情况下，单独一个for循环的复杂度是O(n),但是明显地，这道题不是让你去循环整个数组的。

在有序数组中查找某个元素，一般较好的方法是二分法，因为二分法可以将复杂度降为logN；

 

那么在二分法中，一般会有比较基准值，也就是target，有规定的话，就按照规定来取，没有的话一般按照最左侧或最右侧（也可称为左右端值）取为target，这在左神的算法课里讲过；

在这道题目中是没有目标值的，那么用中间值和低高位（左右端值）进行比较，看处于前半部分的是递增序列还是后半部分的是递增序列（旋转数组，比如说[4,5,6,7,8,1,2,3]前半部分是递增序列[4,5,6,7,8]，后半部分递增序列[1,2,3]），进行操作缩小范围。然后递归在新的范围内再次利用该思想进行查找。

 

在这里我添加一个小栗子，方便大家阅读：

比如：数组[4,5,6,7,8,1,2,3]，数组长度为7，中间元素是数组长,7/2=3，所在位置的元素为7。那么，就该数组就被分为两部分[4,5,6,7]，[8,1,2,3]，前面的数组为递增，不用管，后面的为非递增，所以下一次就在右侧数组里继续查找，那么左端值元素就变为8，右端值元素不变还是3。这种情况就是在右侧查找；

同样的还有在左侧数组查找：

比如数组[7,8,1,2,3,4,5,6]，数组长度为7，中间元素是数组长,7/2=3，所在位置的元素为2。那么，就该数组就被分为两部分[7,8,1,2]，[3,4,5,6]，前面的数组为非递增，后面的为递增，不用管，所以下一次就在左侧数组里继续查找，那么右端元素值就变为2，左端值元素不变还是7。

这里我们把target 看作是左端点，来进行分析，那就要分析以下三种情况，看是否可以达到上述的目标,

• 情况1，数组是[1,2,3,4,5],左端点left的数组下标等于0，右端点right数组下标等于4。数组是递增数组，没有发生扭转。又因为arr[left]<arr[right]，所以最小值就是arr[left]；
• 情况2，数组是[4,5,6,7,8,1,2,3],左端点left的数组下标等于0，右端点right数组下标等于7。arr[left] > arr[right]，发生了扭转。又arr[mid] = 7 > arr[left] = 4， target也就是arr[left]为左端点 4， arr[mid] > target（也就是arr[left]）, 说明[first ... mid] 都是 >= target(也就是arr[left]) 的，因为原始数组是非递减，所以可以确定答案为 [mid+1...last]区间,所以 left= mid + 1；
• 情况3，数组是[5 6 1 2 3 4] ,左端点left的数组下标等于0，右端点数组下标等于5,mid下标是2。arr[mid] = 1 < arr[right]=4 ，arr[mid] 为 1， target为右端点 4， arr[mid] < target（arr[right]）, 说明答案肯定不在[mid+1...right]，但是arr[mid] 有可能是答案,所以答案在[first, mid]区间，所以right = mid;

• 情况4，arr[mid] 既等于arr[left]又等于arr[right]，需要特殊处理。进行left++，如果arr[left] < arr[right] 那么直接返回arr[left]。 

 

如果上述还没看懂，请看下面的解析图：

以array = [4,5,6,7,8,1,2,3]为例：声明：下图中的high 和right一样的意思。

 

 

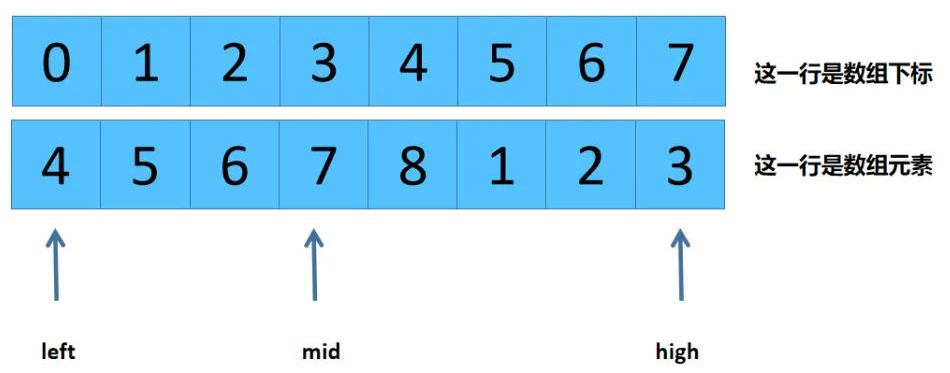
 array[mid] = 7 > array[left] = 4是第二种情况，由于递增最小值只可能在mid的右侧区间，故新的参数： left = mid+1 = 3+1 =4；mid = (left + high)/2 = （4+7）/2 = 5  。新的图画如下：

 

 

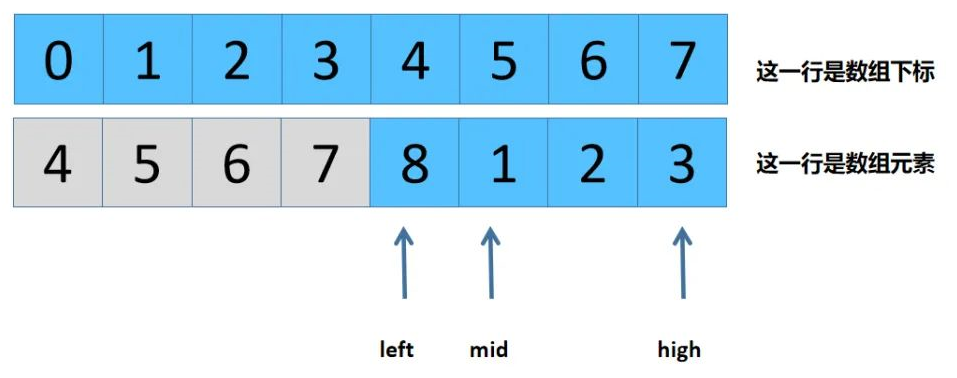
  array[mid] = 5 < array[left] = 8是第三种情况，由于递增最小值只可能在mid的左侧区间（包括mid），故新的参数：  high = mid = 5；mid = (left + high)/2 = （4+5）/2 = 4 。

新的图画如下：

 

 

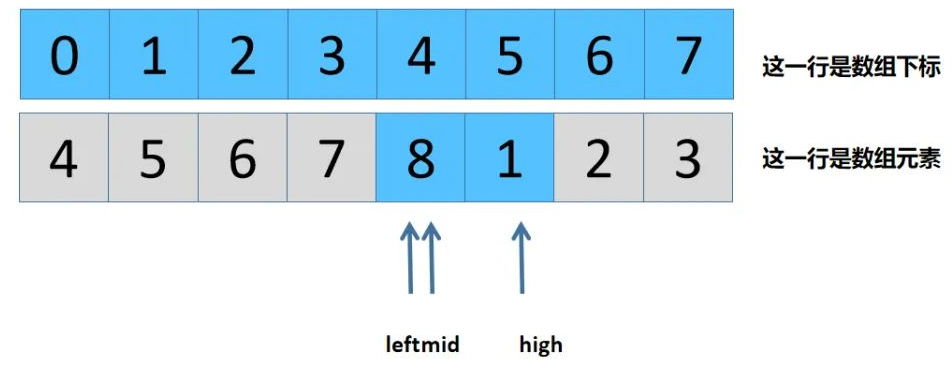
 此时，array[mid] = 8 < array[left] = 8是第四种情况，新的参数如下：    left = left + 1 = 4+1 = 5 ，此时,left = high，故找到最小值，也就是array[5] = 1，跳出循环结束。其实新的图，也可如下看待：

 

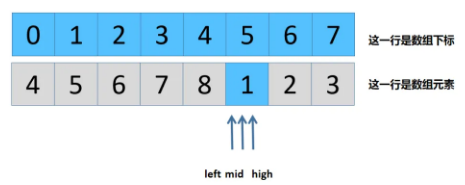
 第四种情况，单独将left++，目的是为了防止像[2,0,2,2,2]类似于这样的数组出现。

如果像这样的数组，那么，根据前述，一开始array[left] = array[mid] 的，前三种情况都不符合。所以需要特殊处理，就是第四种。

其实好好想一想，第二种是array[left] < array[mid] ，第三种是array[left] > array[mid] ，所以肯定还有一种是array[left] = array[mid]。但这个时候你就不能判断最小值是在左区间还是右区间。比如：数组[2,0,2,2,2]中，最小值0就是在左区间；数组[2,2,2,2,2,0,2,2]中，最小值0就是在右区间内。所以，为了确定是在哪一个区间内，我们只好将left+1，这样新的数组也缩小了，就可以继续比对，继续判断新的array[left] 和array[mid] 的大小来确定最小值在哪一侧。原文中关于这一点还有图画，我在这里就不重复叙述了，不懂得可以移步，顺带关注一波原博主，哈哈哈~~~

 

 

Over。。。