左神算法第八节课:介绍递归和动态规划(汉诺塔问题;打印字符串的全部子序列含空;打印字符串的全排列,无重复排列;母牛数量;递归栈;数组的最小路径和;数组累加和问题,一定条件下最大值问题(01背包))
暴力递归:
1,把问题转化为规模缩小了的同类问题的子问题
2,有明确的不需要继续进行递归的条件(base case)
3,有当得到了子问题的结果之后的决策过程
4,不记录每一个子问题的解
动态规划
1,从暴力递归中来
2,将每一个子问题的解记录下来,避免重复计算
3,把暴力递归的过程,抽象成了状态表达
4,并且存在化简状态表达,使其更加简洁的可能
一:递归
1. 汉诺塔问题
汉诺塔问题(不能大压小,只能小压大),打印n层汉诺塔从最左边移动到最右边的全部过程。
左中右另称为 from、to、help。
划分子问题:
1、先把1~n-1从from移动到help;
2、把单独的n移动到to;
3、1~n-1从help移动到to;
时间复杂度就是:T(n) = T(n-1) + 1 + T(n-1) = 2T(n-1)+1(一个等比公式)。T(n-1)是移动到help;1是从from直接移动到to;T(n-1)是把全部n-1挪回去。总的步数是2的N次方减一。

2. 打印一个字符串的全部子序列,包括空字符串
例如:一个字符串awbcdewgh
他的子串:awbc,awbcd,wbcde...很多个子串,但是都是连续在一起
他的子序列:abc,abcd,abcde...很多个子序列,但是子序列中的字符在字符串中不一定是连在一起的
所以 子串!=子序列
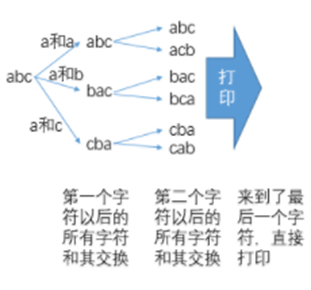
思路:穷举,例如“abc”,一开始返回串res是空字符串,经过第0次,产生有’a’字符的路径和没有’a’字符的路径,经过第1次时,也决定是否有‘b’字符的路径,依次往复,列举所有路径。

1 public class Code_03_Print_All_Subsquences { 2 3 public static void printAllSubsquence2(String str) { 4 char[] chs = str.toCharArray(); 5 process(chs,0); 6 } 7 8 private static void process(char[] chs, int i) { 9 if (i == chs.length) { 10 System.out.print(String.valueOf(chs)+"|"); 11 return; 12 } 13 process(chs, i+1);//有该字符 14 char temp = chs[i]; 15 chs[i] = 0;//将该字符设置成null 16 process(chs, i+1); 17 chs[i] = temp;//复原该字符 18 } 19 20 public static void printAllSub1(char[] str, int i, String res) { 21 if (i==str.length) { 22 System.out.print(res+"|"); 23 return; 24 } 25 // printAllSub1(str, i+1, res);放在这也可以 26 //有该字符的路 27 printAllSub1(str, i+1, res+String.valueOf(str[i])); 28 //没有该字符的路 29 printAllSub1(str, i+1, res); 30 } 31 32 private static void test() { 33 char[] chs = {'a','b','c','d'}; 34 String res = ""; 35 System.out.print("printAllSub1:"); 36 printAllSub1(chs, 0, res); 37 System.out.print("\nprintAllSubsquence2:"); 38 printAllSubsquence2("abcd"); 39 } 40 public static void main(String[] args) { 41 test(); 42 43 } 44 }
结果:

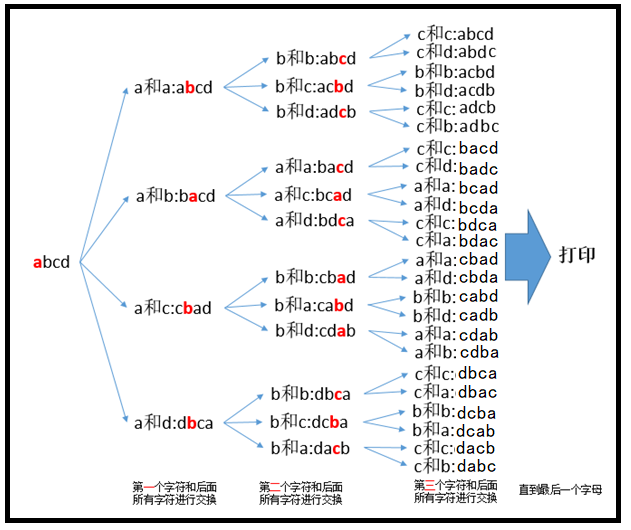
3. 打印一个字符串的全部排列,没有重复排列
1 /** 打印一个字符串的全部排列*/ 2 public class Code_04_Print_All_Permutations { 3 4 public static void printAllPermutations1(String str) { 5 char[] chs = str.toCharArray(); 6 process1(chs, 0); 7 } 8 9 public static void process1(char[] chs, int i) { 10 if (i==chs.length) { 11 System.out.println(String.valueOf(chs)); 12 return; 13 } 14 for (int j = i; j < chs.length; j++) { 15 swap(chs,i,j); 16 process1(chs, i+1); 17 swap(chs, i, j);//要交换过来; 18 } 19 } 20 public static void printAllPermutations2(String str) { 21 char[] chs = str.toCharArray(); 22 process1(chs, 0); 23 } 24 25 private static void swap(char[] chs, int i, int j) { 26 char temp = chs[i]; 27 chs[i] = chs[j]; 28 chs[j] = temp; 29 } 30 31 private static void test() { 32 String test1 = "abc"; 33 printAllPermutations1(test1); 34 System.out.println("======"); 35 // printAllPermutations2(test1); 36 // System.out.println("======"); 37 } 38 public static void main(String[] args) { 39 // TODO Auto-generated method stub 40 test(); 41 } 42 }
4. 母牛数量
母牛每年生一只母牛,新出生的母牛成长三年后也能每年生一只母牛,假设不会死。求N年后,母牛的数量。
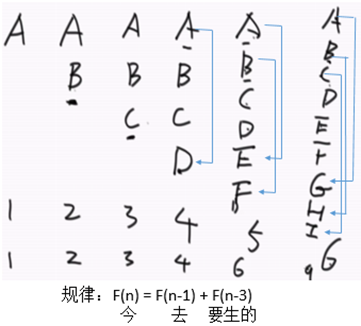
1 /* 2 * 母牛每年生一只母牛,新出生的母牛成长三年后也能每年生一只母牛,假设不会死。 3 * 求N年后,母牛的数量。 4 * 可得每年的:1,2,3,4,6,9... 5 * F(n) = F(n-1) + F(n-3) 6 * 复杂度O(N) 7 * 8 * 改进:矩阵运算O(logN) 9 * 10 */ 11 public class Code_05_Cow { 12 13 //递归 14 public static int cowNumber1(int n) { 15 if (n < 1) { 16 return 0; 17 } 18 if (n == 1 || n == 2 || n == 3) { 19 return n; 20 }else { 21 return cowNumber1(n-1)+cowNumber1(n-3); 22 } 23 } 24 //非递归 25 public static int cowNumber2(int n) { 26 if (n < 1) { 27 return 0; 28 } 29 if (n == 1 || n == 2 || n == 3) { 30 return n; 31 } 32 int cur = 3; 33 int pre = 2; 34 int prepre = 1; 35 int temp1 = 0; 36 int temp2 = 0; 37 for (int i = 4; i <=n ; i++) { 38 temp1 = cur; 39 temp2 = pre; 40 cur = cur + prepre; 41 pre = temp1; 42 prepre = temp2; 43 } 44 return cur; 45 } 46 private static void test() { 47 int i = 10; 48 System.out.print("cowNumber1:"); 49 System.out.println(cowNumber1(i)); 50 System.out.print("cowNumber2:"); 51 System.out.println(cowNumber2(i)); 52 53 } 54 public static void main(String[] args) { 55 test(); 56 57 } 58 }
5. 递归栈
1 public class Code_06_ReverseStackUsingRecursive { 2 3 public static void reverse(Stack<Integer> stack) { 4 if (stack.isEmpty()) { 5 return; 6 } 7 int temp = stack.pop(); 8 reverse(stack); 9 stack.push(temp); 10 11 } 12 private static void test() { 13 Stack<Integer> stack = new Stack<>(); 14 stack.add(1); 15 stack.add(2); 16 stack.add(3); 17 stack.add(4); 18 stack.add(5); 19 stack.add(6); 20 printStack(stack); 21 reverse(stack); 22 printStack(stack); 23 } 24 private static void printStack(Stack<Integer> stack) { 25 for (Integer i : stack) { 26 System.out.print(i+" "); 27 } 28 System.out.println(); 29 } 30 public static void main(String[] args) { 31 test(); 32 33 } 34 }
二:动态规划
1. 数组的最小路径和
给你一个二维数组,二维数组中的每个数都是正数,要求从左上角走到右下角,每一步只能向右或者向下。沿途经过的数字要累加起来。返回最小的路径和。
解题思路:到达右下角时,返回右下角的值;如果到达最后一行,则只能往右走(返回该点处值+右走的值);如果到达最后一列,则只能往下走(返回该点处值+下走的值);计算向右走的总值(该点处值+右走的值),计算向下走的总值(该点处值+下走的值),返回比较值。问题划分为了:向下或者向右的结果,从中选最小的路径,就是最后的答案。


1 //运用递归 2 //从左上角到右下角寻找路径 3 public static int minPath1(int[][] matrix, int i, int j) { 4 if (i == matrix.length - 1 && j == matrix[0].length - 1) { 5 return matrix[i][j]; 6 } 7 if (i == matrix.length - 1) {//到最后一行 8 return matrix[i][j] + minPath1(matrix, i, j + 1); 9 } 10 if (j == matrix[0].length - 1) {//到最后一列 11 return matrix[i][j] + minPath1(matrix, i + 1, j); 12 } 13 int right = matrix[i][j] + minPath1(matrix, i, j + 1); 14 int down = matrix[i][j] + minPath1(matrix, i + 1, j); 15 return Math.min(right, down); 16 } 17 //从右下角到左上角寻找路径 18 public static int minPath2(int[][] matrix) { 19 return process2(matrix, matrix.length - 1, matrix[0].length - 1); 20 } 21 private static int process2(int[][] matrix, int rl, int cl) { 22 if (rl == 0 && cl == 0) { 23 return matrix[rl][cl]; 24 } 25 if (rl == 0 && cl != 0) {//到第一行 26 return matrix[rl][cl] + process2(matrix, rl, cl-1); 27 } 28 if (rl != 0 && cl == 0) {//到第一列 29 return matrix[rl][cl] + process2(matrix, rl-1, cl); 30 } 31 // return matrix[rl][cl] + Math.min(process2(matrix, rl, cl-1), process2(matrix, rl-1, cl)); 32 //等同于以下三句 33 int left = matrix[rl][cl] + process2(matrix, rl, cl-1); 34 int up = matrix[rl][cl] + process2(matrix, rl-1, cl); 35 return Math.min(left,up); 36 }
以上是递归,但是复杂度过高,暴力枚举有待优化:有大量的重复解产生,很多部分都重复计算。如果把重复计算的部分缓存起来,重复的时候直接调用就能省时间,这就是动态规划。如图,当计算到(0,1)位置时,需要计算(0,2)和(1,1),而在计算(1,0)时,需要计算(1,1)和(2,0),此时,(1,1)被重复计算。
什么样的尝试版本递归可以改成动态规划?
当把递归过程展开,发现有重复的状态,与到达它的路径是没有关系的,那么它一定能改成动态规划(无后效性问题)。就本题来说,当到达某点(x,y)时,不管是从上还是从左来的,对于自己来说,从自己到达最右下角的点的最短路径是固定不变的,而与到达(x,y)该处的来源是无关的。
有后效性的是,汉罗塔、N皇后问题(前面的举动会影响后面的结果)。
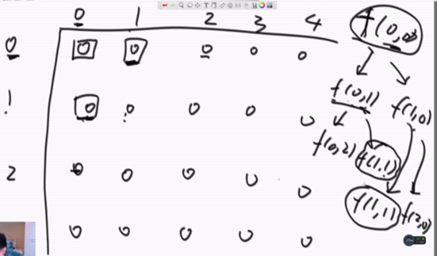
【暴力递归转动态规划过程】对于法1
- 先写出尝试版本;(以从左上角到右下角为例);
- 分析可变参数,那几个可变参数可以代表返回值的状态,可变参数是几维的,dp表就是几维的(该题是i和j二维表);
- 看看最终要的状态是哪一个,在表中点出来(该题是(0,0)位置,五角星处);
- 回到basecase中,把完全不依赖位置的值设置好(这题是最后一行和最后一列);basecase代表一个问题划分到什么程度就不用再划分了(该题是最右下角的位置)。
- 分析一个普遍位置需要哪些位置(该题需要右边的值和下边的值),然后逆着回去,就是填表的顺序。依次计算,推到顶部就是答案。像搭积木一样,堆积到一定条件就能出现答案。
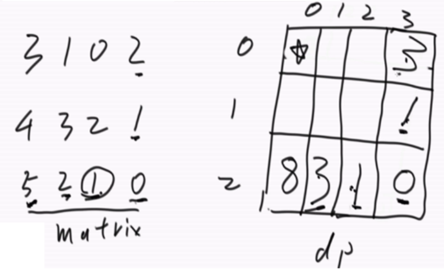

1 //动态规划 2 public static int minPath3(int[][] matrix) { 3 if (matrix==null || matrix.length == 0 4 || matrix[0].length == 0 || matrix[0]==null) { 5 return 0; 6 } 7 int row = matrix.length; 8 int col = matrix[0].length; 9 int[][] dp = new int[row][col]; 10 dp[0][0] = matrix[0][0]; 11 //先把dp表的边界先依次求和填充进去; 12 for (int i = 1; i < row; i++) { 13 dp[i][0] = dp[i-1][0] + matrix[i][0]; 14 } 15 for (int i = 1; i < col; i++) { 16 dp[0][i] = dp[0][i-1]+matrix[0][i]; 17 } 18 //在填充里面的各项;挑选dp表中左边和上边两者中较小的加上matrix[i][j]当前位置,填充dp[i][j]位置; 19 for (int i = 1; i < row; i++) { 20 for (int j = 1; j < col; j++) { 21 dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + matrix[i][j]; 22 } 23 } 24 return dp[row-1][col-1]; 25 }
2. 数组累加问题
给你一个数组arr,和一个整数aim。如果可以任意选择arr中的数字,能不能累加得到aim,返回true或者false。
思路:无后效性,类似于打印所有子序列,就是该位上数字加或不加;
通过分析发现,arr[]和aim是不变的,而i和sum 是变化的,i的范围是数的个数,sum是所有的数的和
1 public class Code_08_Money_Problem { 2 3 public static boolean isSum(int[] arr, int i,int sum,int aim) { 4 if (i == arr.length) { 5 return sum == aim; 6 } 7 return isSum(arr, i+1, sum, aim) || isSum(arr, i+1, sum+arr[i], aim); 8 } 9 private static void test() { 10 int[] arr = {1,4,8}; 11 int aim = 12; 12 System.out.println(isSum(arr, 0, 0, aim)); 13 } 14 public static void main(String[] args) { 15 test(); 16 } 17 }

如:arr[] = [3,2,5]
Return i+1, sum || i+1, sum+arr[i]
推理:
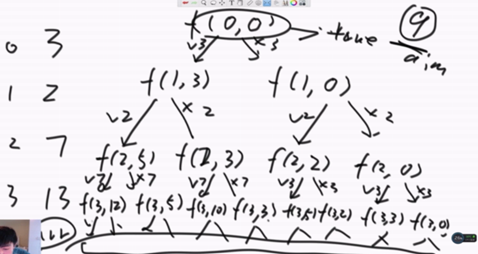
当(i,sum)时,需要的是(i+1,sum)和(i+1,sum+arr[i])
当(2,0),需要的是(3,0)和(3,0+arr[2]),
…像搭积木一样
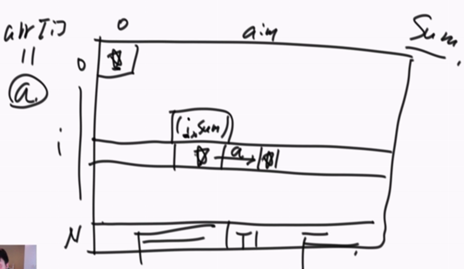
最后一行是多出来的存放结果,只有aim那一列上才
是true,其他都是false。
3. 一定条件下最大值问题
给定两个数组w和v,两个数组长度相等,w[i]表示第i件商品的重量,v[i]表示第i件商品的价值。 再给定一个整数bag,要求你挑选商品的重量加起来一定不能超 过bag,返回满足这个条件下,你能获得的最大价值。
1 public class Code_09_Knapsack { 2 3 public static int maxValue1(int[] c, int[] p, int bag) { 4 return process1(c, p, 0, 0, bag); 5 } 6 7 public static int process1(int[] weights, int[] values, int i, int alreadyweight, int bag) { 8 if (alreadyweight > bag) { 9 return 0; 10 } 11 if (i == weights.length) { 12 return 0; 13 } 14 return Math.max( 15 16 process1(weights, values, i + 1, alreadyweight, bag), 17 18 values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag)); 19 } 20 21 public static int maxValue2(int[] c, int[] p, int bag) { 22 int[][] dp = new int[c.length + 1][bag + 1]; 23 for (int i = c.length - 1; i >= 0; i--) { 24 for (int j = bag; j >= 0; j--) { 25 dp[i][j] = dp[i + 1][j]; 26 if (j + c[i] <= bag) { 27 dp[i][j] = Math.max(dp[i][j], p[i] + dp[i + 1][j + c[i]]); 28 } 29 } 30 } 31 return dp[0][0]; 32 } 33 34 public static void main(String[] args) { 35 int[] c = { 3, 2, 4, 7 }; 36 int[] p = { 5, 6, 3, 19 }; 37 int bag = 11; 38 System.out.println(maxValue1(c, p, bag)); 39 System.out.println(maxValue2(c, p, bag)); 40 } 41 42 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号