bzoj2820--莫比乌斯反演

题目大意：

给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对。

推导：

设n<=m

ans=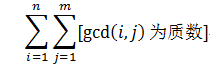 

     =

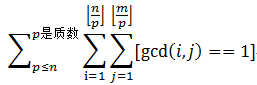
由于gcd(i,j)==1等价于

ans=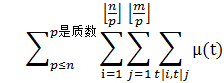

      =

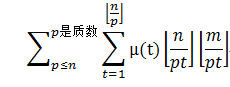
令 T=pt

则ans=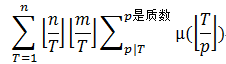

设f(T)=

则f(T)可以用线性筛O(n)预处理出来。

ans=

分块就可以了。总时间复杂度为

具体看代码。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define N 10000001
struct node{
    int x,y;
}a[10001];
inline char nc(){
    static char buf[100000],*p1=buf,*p2=buf;
    if(p1==p2){
        p2=(p1=buf)+fread(buf,1,100000,stdin);
        if(p1==p2)return EOF;
    }
    return *p1++;
}
inline void read(int& x){
    char c=nc(),b=1;
    for(;!(c>='0'&&c<='9');c=nc());
    for(x=0;c>='0'&&c<='9';x=x*10+c-48,c=nc());x*=b;
}
int len;
char c[20];
inline void print(long long x){
    if(!x){
        putchar('0');
        putchar('\n');
        return;
    }
    for(len=0;x;x/=10)c[++len]=x%10;
    for(;len;len--)putchar(c[len]+'0');
    putchar('\n');
}
inline int Min(int x,int y){
    return x<y?x:y;
}
int p[N],tot,t,i,j,k,n,m,mu[N],y,T,ma,x;
long long ans,f[N];
bool v[N];
int main()
{
    read(T);
    for(i=1;i<=T;i++){
        read(a[i].x);read(a[i].y);
        if(a[i].y<a[i].x){t=a[i].x;a[i].x=a[i].y;a[i].y=t;}
        if(a[i].x>ma)ma=a[i].x;
    }
    mu[1]=1;
    for(i=2;i<=ma;i++){
        if(!v[i]){
            p[++tot]=i;
            mu[i]=-1;
        }
        for(j=1;j<=tot&&p[j]*i<=ma;j++){
            v[i*p[j]]=1;
            if(i%p[j])mu[i*p[j]]=-mu[i];else{
                mu[i*p[j]]=0;
                break;
            }
        }
    }
    for(i=1;i<=tot;i++)f[p[i]]++;
    for(i=2;i<=ma;i++)
    for(j=1;p[j]*i<=ma;j++)
    f[i*p[j]]+=mu[i];
    for(i=2;i<=ma;i++)f[i]+=f[i-1];
    for(x=1;x<=T;x++){
        i=1;ans=0;
        while(i<=a[x].x){
            j=Min(a[x].x/(a[x].x/i),a[x].y/(a[x].y/i));
            ans+=(f[j]-f[i-1])*(a[x].x/i)*(a[x].y/i);
            i=j+1;
        }
        print(ans);
    }
    return 0;
}