粒子群算法求一元函数最值问题

在上一篇详细介绍粒子群算法实现分组背包的随笔中，已经详细介绍了粒子群算法的主要思想，如果掌握了用粒子群算法如何实现分组背包的话，那么要将其修改成一元函数求最值的应用简直易如反掌。这里如下先copy一份之前总结的用粒子群算法实现分组背包大致思想：

• 随机产生了一堆粒子，每个粒子代表背包的一种情况（选了哪3个物品），初始粒子全都是局部最优粒子。
• 计算每个粒子的适应度值（也就是每个粒子代表的背包的价值、体积、重量），然后每个粒子适应度按优劣选出非劣粒子。
• 之后进入迭代过程，每次迭代中，从非劣粒子中随机选一个作为全局最优粒子，按照公式计算粒子速度（跟较优粒子和全局最优粒子息息相关），使每个粒子产生移动（也就是有概率替换代表的物品）。
• 如果移动后的粒子比之前的粒子更优则替代原来的局部最优粒子
• 然后把非劣粒子和局部最优粒子放一起，再按优劣选出非劣粒子
• 去除重复的非劣粒子，进入下一次迭代。

现在针对求一元函数最小值对上述思想做出如下改动：

• 随机产生了一堆粒子，每个粒子代表一个横坐标，初始粒子全都是局部最优粒子。
• 计算每个粒子的适应度值（也就是每个粒子代表的纵坐标值），然后每个粒子适应度按优劣选出初始非劣粒子。
• 之后进入迭代过程，每次迭代中，从非劣粒子中随机选一个作为全局最优粒子，按照公式计算粒子速度（跟较优粒子和全局最优粒子息息相关），使每个粒子产生移动（也就是横坐标左移或右移）。
• 如果移动后的粒子比之前的粒子更优则替代原来的局部最优粒子
• 然后把非劣粒子和局部最优粒子放一起，再按优劣选出非劣粒子
• 去除重复的非劣粒子，进入下一次迭代。

---

一：一元函数最值问题

假设有如下函数：

\[y(x) = sin(x^2) - 2sin(x) + x * sin(x) \]

画出该函数的图像如图所示：

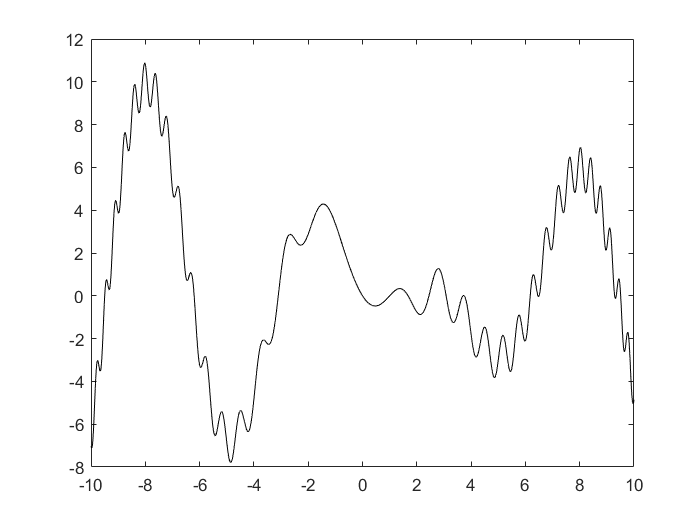
我们要如何找到函数在[-3, 9]之间的最小值呢？首先放一个展示粒子群如何找到最小值的动态图：

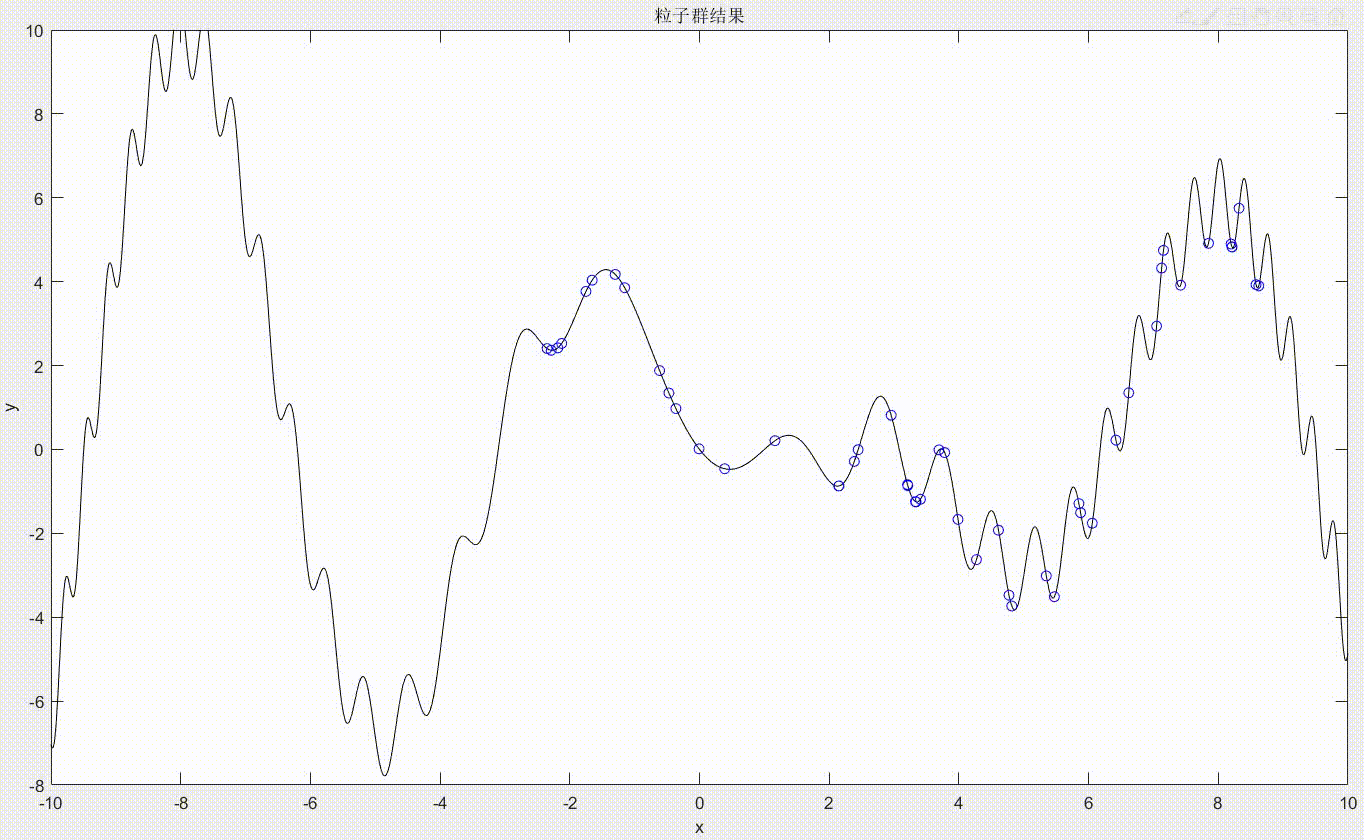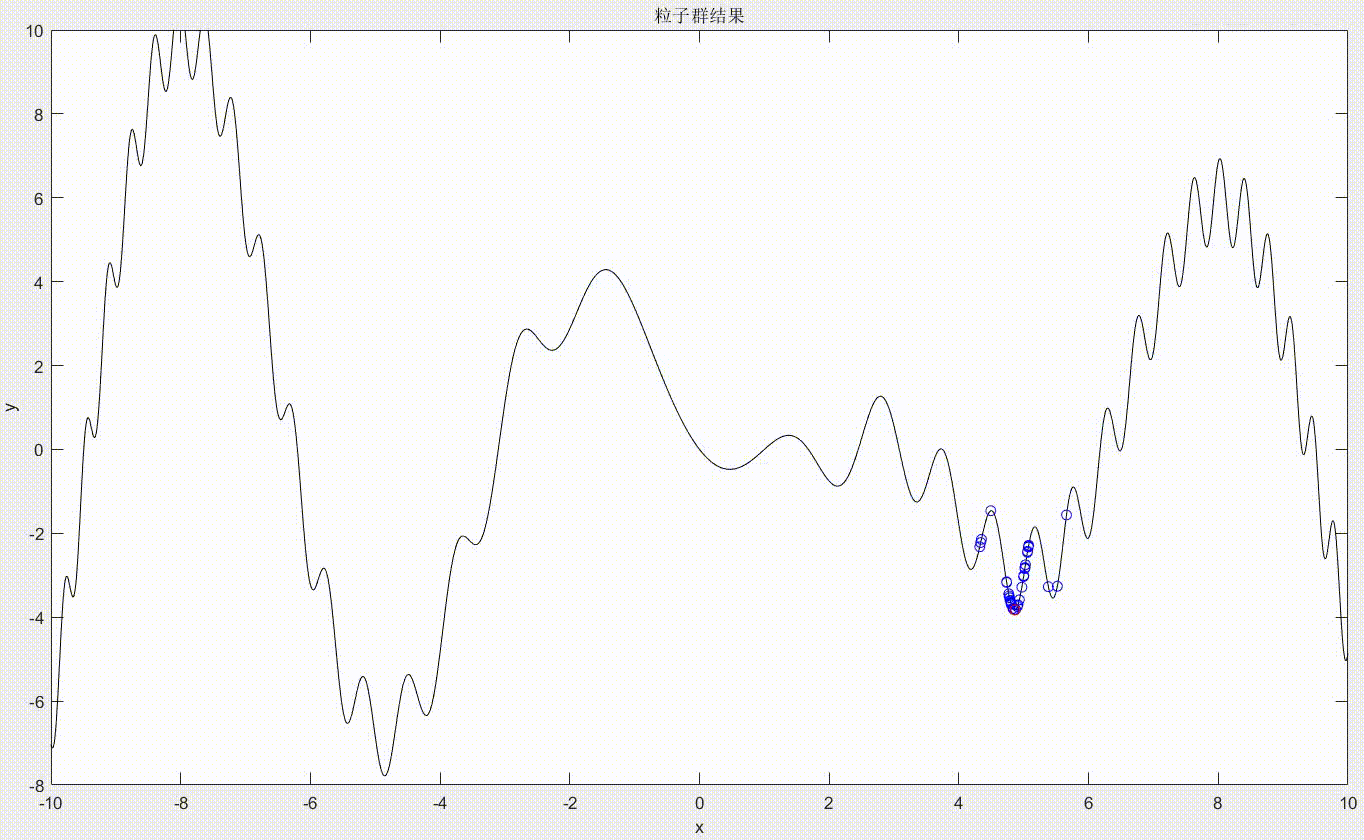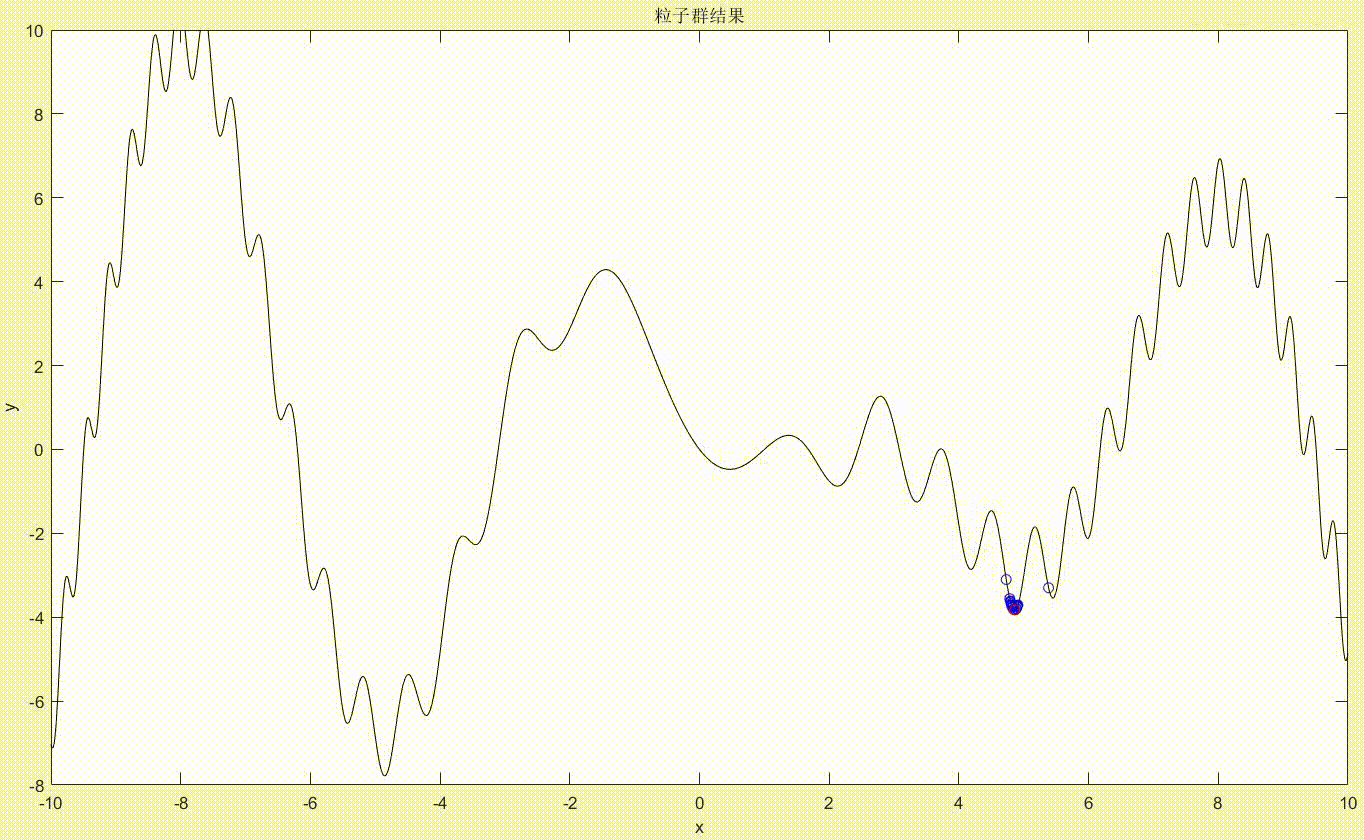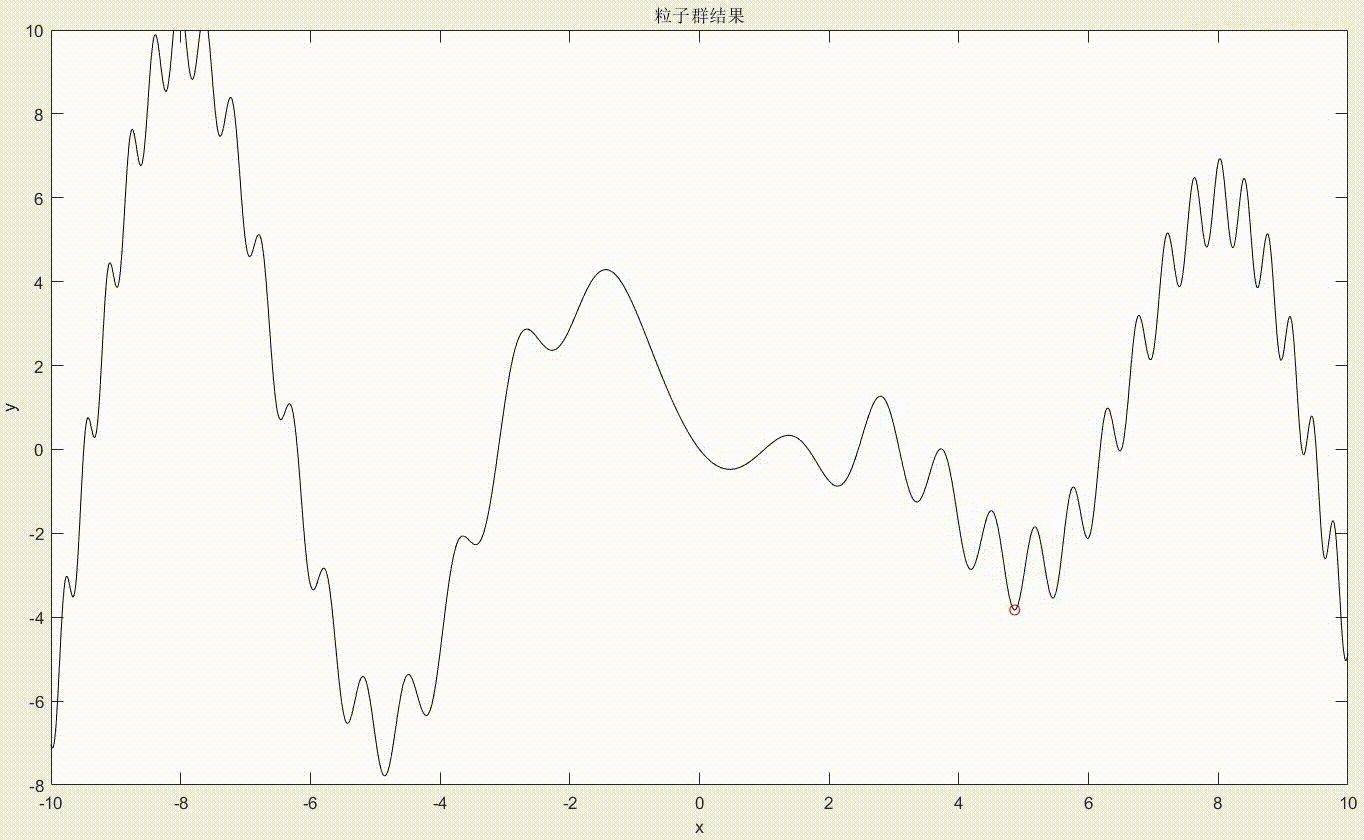
从图中可以看到，我们先生成了50个粒子，用蓝色小点表示，用红色小点表示非劣解粒子（最后的最小值点一定是包括在非劣解粒子中的），但这里可以看到非劣解粒子一直只有一个，所以它就是我们所求的最小值点。可以看到每次迭代粒子的位置都会变化，并不断向最小值位置处移动。

下面具体介绍下粒子群算法如何求一元函数最值。还是按照上一篇随笔一样将完整的MATLAB代码分解成七部分讲解。

---

二：粒子群算法求一元函数最值问题

2.1 输入参数、固定参数初始化

注意参数中的惯性权值可以自己修改成自己觉得合适的值，它会影响粒子每次运动的步长。wmax越大迭代初期粒子运动步长越大；wmin越小迭代末期粒子运动步长越小。

clear, clc, close all;

%% 输入参数、固定参数初始化
xsize = 50;         % 粒子数
ITER = 50;         % 迭代次数
c1 = 0.8; c2 = 0.8;      % 常数
wmax = 1.0; wmin = 0.01;  % 惯性权重相关常数
v = zeros(1, xsize); % 粒子速度初始化

2.2 粒子群位置、适应度、最佳位置、最佳适应度初始化

随机产生粒子群\(x\)，表示每个粒子的横坐标，注意想要产生\([a, b]\)之间的均匀分布随机数的话，就用\(a + (b - a) * rand(1,1)\)这个表达式。

适应度其实就是用粒子群的纵坐标。

%% 粒子群位置、适应度、最佳位置、最佳适应度初始化
x = -3 + 12 * rand(1, xsize); % 随机粒子群位置生成（表示横坐标[-3, 9]）

% 粒子群适应度
y = zeros(1, xsize); % 粒子群纵坐标
for i = 1 : xsize
    y(i) = sin(x(i).^2) - 2*sin(x(i)) + x(i) * sin(x(i));
end

bestx = x; % 粒子群位置最佳值
besty = y; % 粒子群最佳适应度

2.3 初始筛选非劣解

第一次筛选非劣解，之后每次迭代都会重新筛选一次。其中的判断条件很重要，可以根据问题的限制而改变。这里就是判断每个粒子是否比别的所有粒子都更符合要求（纵坐标更小）。

%% 初始筛选非劣解
cnt = 1;
for i = 1 : xsize
    fljflag = 1;
    for j = 1 : xsize
        if j ~= i
            if y(i) > y(j) % i为劣解
                fljflag = 0;
                break;
            end
        end
    end 
    if fljflag == 1
        flj(cnt) = y(i); % 非劣解适应度
        fljx(cnt) = x(i); % 非劣解位置
        cnt = cnt + 1;
    end
end

2.4 粒子运动计算

粒子速度的计算还是依照如下经典公式：

\[v^{i+1} = wv^i + c1r1(p_{local}^i - x^i) + c2r2(p_{global} - x^i) \]

其中\(w\)为惯性权值，\(c1\)和\(c2\)为常数，\(r1\)和\(r2\)为[0，1]间服从均匀分布的随机数，\(p_{local}^i\)是局部最优粒子；\(p_{global}\)是全局最优粒子，注意只有一个全局最优所以没有上标\(i\)。

惯性权值的取值跟迭代次数有关，这里我们采用\(w = wmax-(wmax - wmin) * niter / iterall\)这样的计算方法。相关惯性权值的计算也是粒子群算法研究的热点，惯性权值变化大，粒子速度快，位置变换也快，惯性权值取得好的话可以使粒子群更快的收敛到全局最优！

在用速度对每个粒子位置进行更新时，注意一个问题，就是不要让运动后的粒子横坐标超过我们的判断区间\([-3, 9]\)了。

for niter = 1 : ITER % 迭代开始，粒子开始运动
    xx = [-10 : 0.01 : 10]; % 画图用
    yy = sin(xx.^2) - 2*sin(xx) + xx .* sin(xx);
    plot(xx, yy, 'k');
    xlim([-10, 10]);ylim([-8, 10]);
    title('粒子群结果'); xlabel('x'); ylabel('y');
    hold on;
    
    rnd = randi(length(flj), 1, 1);
    gbest = fljx(rnd); % 粒子全局最优解
    
    %% 粒子运动计算
    w = wmax - (wmax - wmin) * niter / ITER; % 惯性权值更新
    r1 = rand(1,1); r2 = rand(1,1); % 产生$[0, 1]$间均匀分布随机值
    for i = 1 : xsize
       v(i) = w * v(i) + c1 * r1 * (bestx(i) - x(i)) + c2 * r2 * (gbest - x(i)); % 粒子速度
       x(i) = x(i) + v(i);
       
       if (x(i) > 9 || x(i) < -3); % 运动后x范围超过了，用新的随机数代替
          x(i) = -3 + 12 * rand(1, 1);
       end
    end

2.5 当前粒子群适应度、最佳位置、最佳适应度

粒子经过了运动到了新的位置，当然要把新粒子和旧粒子拿出来比一比，如果新粒子的适应度比旧粒子好的话（纵坐标更小），就更新局部最佳粒子位置。不像背包问题那样要考虑多个判断条件，这里的判断相当简单，也不用管其他的情况。

    y_cur = zeros(1, xsize);                                 
    for i = 1 : xsize
        y_cur(i) = sin(x(i).^2) - 2 * sin(x(i)) + x(i) * sin(x(i));
    end
    
    for i = 1 : xsize
        if y_cur(i) < y(i) % 如果当前粒子适应度更好
            bestx(i) = x(i); % 粒子最佳位置更新
            besty(i) = y_cur(i);% 粒子最佳适应度更新       
        end
    end
    
    y = y_cur; % 新粒子变成旧粒子

2.6 粒子群最佳位置、最佳适应度合并后再筛选非劣解

与第一次做非劣解筛选的步骤基本一样，只是加了一个合并操作，把局部最佳粒子与非劣解粒子合并在一起，然后再筛选一波非劣解粒子。

    %% 粒子群最佳位置、最佳适应度合并后再筛选非劣解
    bestxmerge = [bestx, fljx];
    ymerge = [besty, flj];

    n = length(flj);
    flj = [];
    fljx = [];
    cnt = 1;
    for i = 1 : xsize + n 
        fljflag = 1;
        for j = 1 : xsize + n
            if j ~= i
                if ymerge(i) > ymerge(j) % i为劣解
                    fljflag = 0;
                    break;
                end
            end
        end 
        if fljflag == 1
            flj(cnt) = ymerge(i); % 非劣解适应度
            fljx(cnt) = bestxmerge(i); % 非劣解位置
            cnt = cnt + 1;
        end
    end

2.7 去掉重复非劣解

这一步也很重要，实现方法也有很多，随便选一种把重复的非劣解去掉就可以咯。

    %% 去掉重复非劣解
    issame = zeros(cnt - 1, 1);
    for i = 1 : cnt - 1
        for j = i + 1 : cnt - 1
            if ~issame(j)
                issame(j) = (abs(fljx(j) - fljx(i)) < 0.0001);
            end
        end
    end
    flj(find(issame == 1)) = [];
    fljx(find(issame == 1)) = [];
            
    
    plot(bestxmerge, ymerge, 'bo'); % 画粒子群最优位置
    plot(fljx, flj, 'ro'); % 画非劣解位置
    pause(0.5);
    hold off;
end