矩阵QR分解的MATLAB与C++实现
一:矩阵QR分解
矩阵的QR分解目的是将一个列满秩矩阵\(A\)分解成\(A=QR\)的形式,我们这里暂时讨论\(A\)为方阵的情况。其中\(Q\)为正交矩阵;\(R\)为正线(主对角线元素为正)上三角矩阵,且分解是唯一的。
比如\(A= \begin{bmatrix} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \\ \end{bmatrix}\),我们最终要分解成如下形式:
\[A=Q \cdot R =
\begin{bmatrix}
\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{2}} \\
\frac{2}{\sqrt{6}} & -\frac{1}{\sqrt{3}} & 0 \\
\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{2}} \\
\end{bmatrix}
\cdot
\begin{bmatrix}
\sqrt{6} & \sqrt{6} & \frac{7\sqrt{6}}{6} \\
0 & \sqrt{3} & \frac{\sqrt{3}}{3} \\
0 & 0 & \frac{\sqrt{2}}{2} \\
\end{bmatrix}
\]
现在主要的问题是如何由矩阵\(A\)计算得到矩阵\(Q\)和\(R\)呢?我们将在下面讨论。
1.1 QR分解原理
在线性代数或矩阵理论中,我们肯定都学过斯密特正交化(Gram-Schmidt Orthogonalization),正交化过程即将欧氏空间的任一基化为标准正交基,构造出的标准正交基正好构成了我们想要的\(Q\)矩阵,而\(R\)矩阵由正交化过程的公式倒推即可得到。
首先假设初始方阵为\(A\),\(\vec{x_i}\)、\(\vec{y_i}\)、\(\vec{z_i}\)都为列向量。我们学过斯密特正交化的步骤如下:
\[A=\begin{bmatrix}
\vec{x_1} & \vec{x_2} & \vec{x_3}
\end{bmatrix}
\overset{正交化}{\underset{}{\to}}
\begin{bmatrix}
\vec{y_1} & \vec{y_2} & \vec{y_3}
\end{bmatrix}
\overset{单位化}{\underset{}{\to}}
\begin{bmatrix}
\vec{z_1} & \vec{z_2} & \vec{z_3}
\end{bmatrix}
= Q
\]
再具体一点(为了好写,之后的\(\vec{x_i}\)、\(\vec{y_i}\)、\(\vec{z_i}\)都不加箭头了,默认为列向量):
\[y_k = x_k - \sum_{i=1}^{k-1} \frac{(x_k,y_i)}{(y_i,y_i)}y_i =
x_k - \sum_{i=1}^{k-1} \frac{(x_k,y_i)}{||y_i||^2}y_i =
x_k - \sum_{i=1}^{k-1} (x_k,z_i)z_i \tag{1}
\]
\[z_k = \frac{y_k}{||y_k||} ,k=1...n \tag{2}
\]
\[Q = \begin{bmatrix}
z_1 & \cdots & z_n \tag{3}
\end{bmatrix}
\]
\[R= \begin{bmatrix}
||y_1|| & (x_2,z_1) & \cdots & (x_n,z_1) \\
& ||y_2|| & \cdots & (x_n,z_2) \\
& & \ddots & \vdots\\
\mathsf 0 & & &||y_n||
\end{bmatrix} \tag{4}
\]
由上述公式写出计算\(Q\)和\(R\)的伪代码为:
\[\begin{align}
& for \quad k=1:n \notag\\
& \qquad R_{kk}=||A_{:k}|| \notag\\
& \qquad Q_{:k}=A_{:k} / R_{kk} \notag\\
& \qquad for \quad i = k + 1 : n \notag\\
& \qquad \qquad R_{ki} = A_{:i}' * Q_{:k} \notag\\
& \qquad \qquad A_{:i} = A_{:i} - R_{ki} .* Q_{:k} \notag\\
& \qquad end \notag\\
& end \notag\\
\end{align}
\]
注:\(A_{:k}\)表示\(A\)的第\(k\)列向量。
可以看出其实矩阵的QR分解的步骤并不多,就是不断地循环进行\(A\)的正交化、标准化、求\(Q\)、求\(R\)这几步。
二:矩阵QR分解的MATLAB实现
clc, clear all, close all
% 矩阵的QR分解
A = [1 2 2;2 1 2;1 2 1] % 考虑非奇异方阵
[m,n] = size(A);
Q = zeros(n,n);
X = zeros(n,1);
R = zeros(n);
for k = 1 : n
R(k,k) = norm(A(:,k)); % 计算R的对角线元素
Q(:,k) = A(:,k) / R(k,k); % A已正交化,现在做标准化,得到正交矩阵Q
for i = k + 1 : n
R(k,i) = A(:,i)' * Q(:,k); % 计算R的上三角部分
A(:,i) = A(:,i) - R(k,i) .* Q(:,k); % 更新矩阵A,斯密特正交公式
end
end
Q
R
三:矩阵QR分解的C++实现
#include <iostream>
#include <vector>
using namespace std;
int main() /* 矩阵A的QR分解*/
{
vector<vector<double>> a = { {1,2,2},{2,1,2},{1,2,1} };
int n = a.size();
vector<vector<double>> q(n, vector<double>(n));
vector<vector<double>> r(n, vector<double>(n));
cout << "A:" << endl; //输出矩阵A
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf("%.4f ", a[i][j]);
}
cout << endl;
}
for (int k = 0; k < n; k++)
{
double MOD = 0;
for (int i = 0; i < n; i++)
{
MOD += a[i][k] * a[i][k];
}
r[k][k] = sqrt(MOD); // 计算A第k列的模长,由公式(4)等于R的对角线元素||A:k||
for (int i = 0; i < n; i++)
{
q[i][k] = a[i][k] / r[k][k]; // 由公式(2),A第k列标准化之后成为Q的第k列
}
for (int i = k + 1; i < n; i++)
{
for (int j = 0; j < n; j++)
{
r[k][i] += a[j][i] * q[j][k]; // 由公式(4),计算R的上三角部分
}
for (int j = 0; j < n; j++)
{
a[j][i] -= r[k][i] * q[j][k]; // 由公式(1),计算更新A的每一列
}
}
}
cout << endl;
cout << "Q:" << endl; //输出矩阵Q
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf("%.4f ", q[i][j]);
}
cout << endl;
}
cout << endl;
cout << "R:" << endl; //输出矩阵R
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf("%.4f ", r[i][j]);
}
cout << endl;
}
return 0;
}
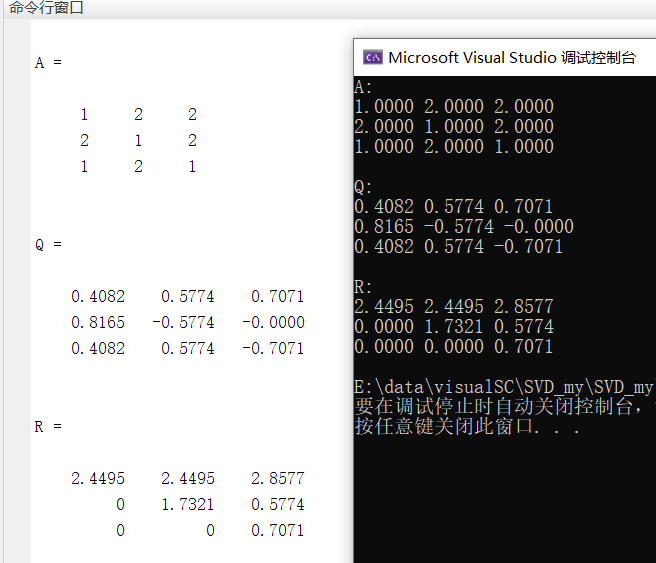
四:结果对比
由下图可以看到,由MATLAB和C++计算出的\(Q\)和\(R\)矩阵完全相同。