两种频率调制(FM)方法的MATLAB实现
详细讲解了FM调制原理与实现、非相干解调原理与实现、希尔伯特变换的由来、相干解调原理与实现、锁相环的应用。
为什么要写这一篇文章呢？其实最开始我只是想学习下锁相环，然后用MATLAB做一下仿真什么的。但我认为最好的学习方法是找一个简单的应用，这应用里要用到锁相环的相关知识。我想到了频率调制在同步解调时可能会用到它，于是去查找了相关资料，实现了部分内容并写下了这篇文章，文章中为了完整的展现整个过程，索性将完整的FM调制解调都总结了一下。为了说明代码的计算原理，也进行了一些相关知识的补充。
一: 频率调制
1.1 要实现什么
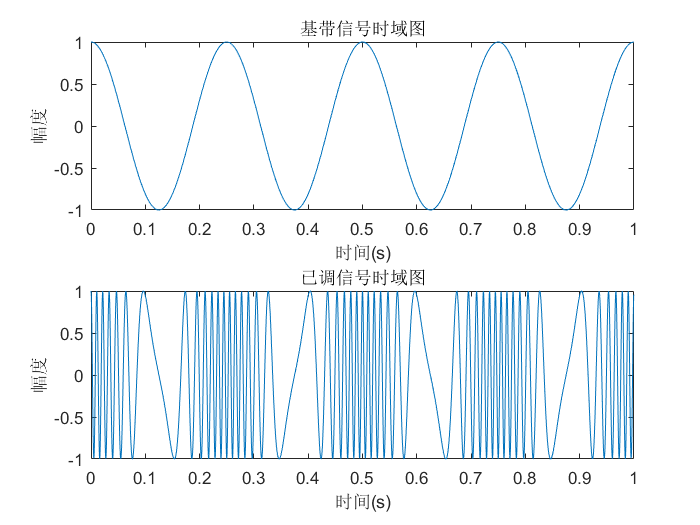
在通信原理这门课中，我们学习知道了频率调制FM的目的，是用载波的频率大小来表示基带信号幅度的大小。比如下面这幅图，可以看到我们想要实现得到一个已调波，基带信号幅度上升时，已调波频率增加；基带信号幅度下降时，已调波频率减小。
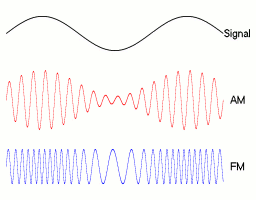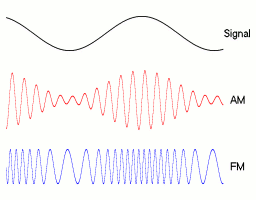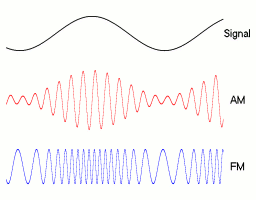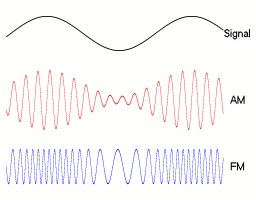
1.2 原理与实现
那么如何用基带信号的幅度来控制已调波的频率呢？那我们就人为的把他俩扯上关系吧。下面是一个把他俩扯上关系的实现过程：
首先我们假设基带信号为\(m(t)\)，载波频率为\(f_c\)，载波振幅为\(A_c\)。我们倒着推，直接假设已调波\(S_{FM}(t)\)为：
瞬时频率为\(f_k = 2\pi f_c + \frac{d\phi(t)}{dt}\)
瞬时频偏为\(\frac{d\phi(t)}{dt}\)
把瞬时频偏和信号的幅度扯上关系，便满足了这一节刚开始我们的想法。设下面关系式：
其中\(K_f\)为频偏常数，表示调频器的调频灵敏度。
将(2)代回(1)里面，得到已调波的真正表达式为：
更进一步，假设基带信号为余弦波\(m(t) = cos(2 \pi f_m t)\)，\(A_c = 1\)，已调波的表达式为：
顺利推导出了已调波的表达式，调制部分差不多就结束了，我们直接根据表达式写代码就好了。
Fs = 2000; % 采样频率
Ts = 1 / Fs;
L = 2000; % 取2000采样点，1s
t = (0 : L - 1) * Ts;
kf = 45; % 调频灵敏度
fm = 4; % 基带信号频率
fc = 50; % 载波频率
mt = cos(2 * pi * fm * t); % 基带信号
st = cos(2 * pi * fc * t + kf * sin(2 * pi * fm * t) / fm); % 由公式(5)写出已调FM信号
% st = cos(2 * pi * fc * t + 2 * pi * kf * cumsum(mt) * Ts); % 也可由公式(4)写出已调FM信号
下图是基带信号和已调信号波形图：
二: 非相干解调
现在基带信号已经调制完毕了。我们不考虑噪声的问题，之后该如何从已调信号恢复我们想要的基带信号呢？首先我们使用非相干解调的方法，顾名思义，使用非相干解调的话，我们就不用进行把已调信号和本地载波相乘的操作，也不用使用锁相环。但我们需要对已调信号做微分和使用一点点希尔伯特变换相关的知识，下面将进行详细讲解。
2.1 要实现什么
我们要想办法从已调信号中恢复出\(m(t)\)来，对公式\((3)\)的\(S_{FM}(t)\)求微分，得到：
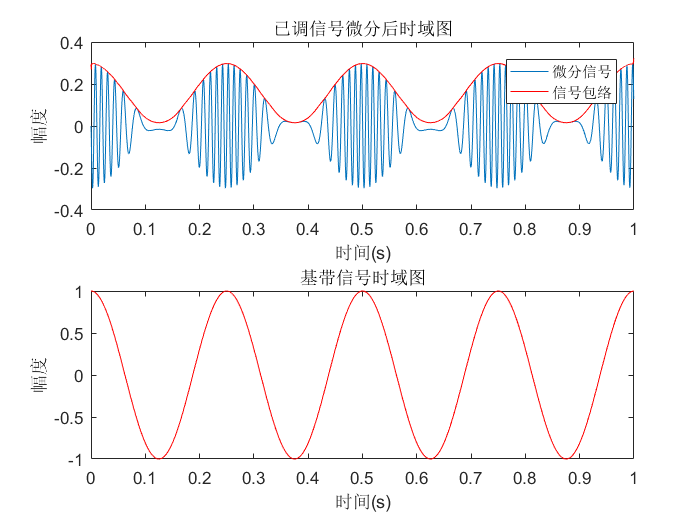
一般假设\(A_c = 1\)，现在我们就要思考了，要是我们能将\(S_d(t)\)的包络\(2 \pi f_c + K_f m(t)\)通过某种方式提取出来，那么我们不就能轻易的恢复\(m(t)\)了吗？没错，接下来我们就要用希尔伯特变换和解析信号的性质来提取包络了！
等下！我们先来看看结论，如图可知如果我们能够提取出包络，便能很容易的恢复基带信号了，你看包络和基带信号长得多像，只是振幅小了些，增加了直流分量而已。
2.2 希尔伯特变换(包络检波原理)
这里补充一些希尔伯特变换的相关知识。首先为什么研究学者要引入希尔伯特变换这个玩意儿呢？它其实是有实际的现实意义的。
一般我们在计算某一信号的频谱时，我们会发现信号除了正的频率外，还有对称的另一半负频率，比如上面公式\((6)\)的微分信号\(S_d(t)\)的频谱图如下所示：
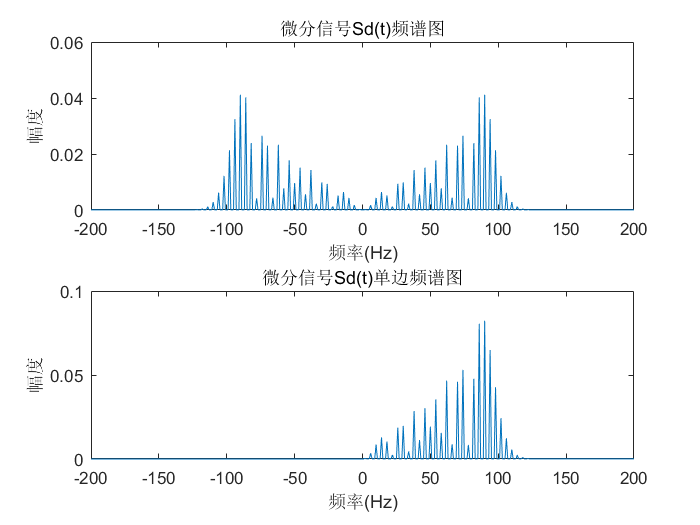
我们设某一信号的频谱为\(X(f)\)，如果我们想去掉负频率部分，并且能量不变的话，我们可以将原频谱的2倍乘以阶跃函数\(U(f)\)，于是有：
上式是频域的变化，那时域是如何变的呢，由傅里叶逆变换得到：
于是我们知道了，想要除去信号的负频率部分，只需要用该信号与\(\frac{1}{\pi t}\)的卷积乘以i，再加上该信号即可。一般我们把\(\widetilde x(t)\)叫做\(x(t)\)的解析信号；把\(x(t) * \frac{1}{\pi t}\)叫做\(x(t)\)的希尔伯特变换。
上面就是希尔伯特变换的来源和作用了（这是附加内容，了解下就可以了），定义希尔伯特变换:
定义解析信号：
那么如何用解析信号来求包络呢？
假设包络为\(a(t)\)，载波为\(cos(2\pi f_0 t + \theta(t))\)，已调信号\(x(t) = a(t)cos(2\pi f_0 t + \theta(t))\)。
解析信号为：
取解析信号的模：
可以看到我们成功提取出了包络来。其实整个过程就是我们构造解析信号，然后利用的希尔伯特变换的正交性，从已调信号中提取出包络。
2.3 包络检波实现
由上面的原理我们已经知道了如何从已调信号中提取出包络来，直接上实现代码吧。代码超简单，就两行QAQ。注意MATLAB中的hilbert函数是求解析信号而不是求希尔伯特变换，要得到希尔伯特变换的话由（10）可知，取其中的虚部就可以了。
sdt = [0 diff(st)]; % 先对已调信号做微分
rt = abs(hilbert(sdt)); % 再构造解析信号求包络,得到非相干解调信号
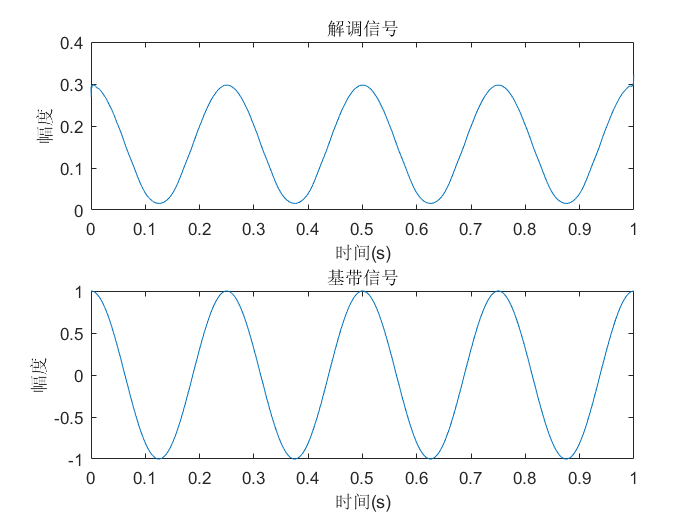
从上图可以看到我们已经基本恢复了基带信号，剩下的只需做一下隔直流和把信号放大就可以了。注意：解调信号振幅为什么变小呢？因为在MATLAB做微分时，用函数diff()并不能对时间间隔取到无穷小。
三: 相干解调(同步解调)
在这一部分中，要考虑用另外一种FM解调方式了，就是利用锁相环(PLL)进行相干解调。锁相环的作用之一便是在信号解调方面的应用。对于锁相环的原理和实现，参考了很多相关资料，在下面是我的一个粗浅的总结。
3.1 锁相环功能与结构
锁相环是一种相位反馈跟踪系统。鉴相器输出的相位误差信号经过环路滤波器滤波后，作为压控振荡器的控制信号，而压控振荡器的输出又反馈到鉴相器，在鉴相器中与输入信号进行相位比较。压控振荡器的输出信号相位将跟踪输入信号的相位变化，这时压控振荡器输出信号的频率与输入信号频率相等，而相位保持一个微小误差。
PLL一般用于：
- 载波同步
- FM解调
这里我们直接按照FM解调的数学模型讨论。框图如下：
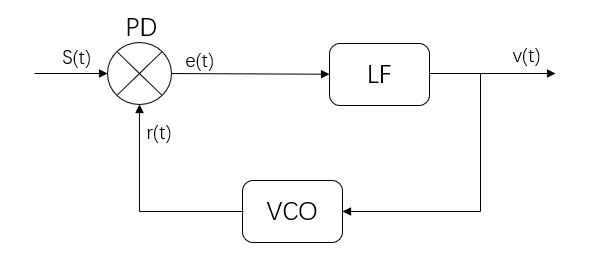
PLL主要包括3部分：
-
压控振荡器VCO(Voltage Controlled Oscillator)：根据输入信号大小的不同，输出频率不同的的正弦波。
-
乘法鉴相器PD(Phase Detector)：将已调信号\(s(t)\)与VCO的输出信号\(r(t)\)相乘。
-
环路滤波器LF(Loop Filter)：低通滤波器，将PD输出的高频分量滤除。
3.2 要实现什么
锁相环所要实现的是：给我们一个输入信号\(s(t)\)，\(s(t)\)的瞬时相位可能是在不断变化着的，但我们通过这样一个锁相环结构，使得VCO的输出\(r(t)\)的瞬时相位跟随和追踪\(s(t)\)，当跟踪成功时，这时\(r(t)\)基本上和\(s(t)\)一个样，此时我们也能从环路中恢复出基带信号\(m(t)\)了，具体如何恢复的见下面推导。
3.3 锁相环各部分公式推导
3.3.1 VCO部分
我们由公式（3）已知输入的FM已调波为(正弦余弦都可以，为了好说明，这里用正弦):
其中
一般假定VCO的固有振荡频率为载波频率\(f_c\)，设由本地VCO跟踪产生的FM信号为：
其中
\(A_v\)为VCO载波幅度，\(K_v\)为VCO的频率灵敏度。从公式的角度，锁相环的目的就是不断调整\(v(t)\)，使得\(\phi_2(t)\)尽可能等于\(\phi_1(t)\)
3.3.2 PD部分
将输入的已调波\(s(t)\)与本地FM波相乘，会得到两个分量。
3.3.3 LF部分
通过低通滤波器，滤去\(e(t)\)的高频分量，输出为\(v(t)\)。
\(K_m\)为鉴相器增益；\(\phi_e(t) = \phi_1(t) - \phi_2(t)\)，为相位误差。
当\(\phi_e(t) = 0\)，就说PLL处于锁定状态；当\(\phi_e(t) < 1 rad\)，就说PLL处于接近锁定状态，并且可以近似运算\(sin(\phi_e(t)) \approx \phi_e(t)\)。所以(17)进一步写为：
由于\(\phi_2(t)\)在不断跟踪\(\phi_1(t)\)，所以处于稳定状态时，\(\phi_e(t) =0\)，\(\phi_2(t) = \phi_1(t)\)，由公式(13)(15)可得：
就能用\(v(t)\)恢复\(m(t)\)了。
3.3.4 低通滤波器原理与实现补充
在PLL中会用到低通滤波器，为了之后能看懂低通滤波的代码，这里介绍一下IIR滤波器原理，如何使用滤波系数进行滤波，以及如何使用MATLAB的FDA工具获取滤波系数，这里想多总结一点，不想看的话可以有个印象即可。
通常系统(线性时不变离散系统)输入输出之间的运算关系可由N阶线性常系数差分方程来描述：
比如当\(M = 0\)且\(N = 1\)，系统为\(y[n] = b_0x[n] -a_1y[n - 1]\)。
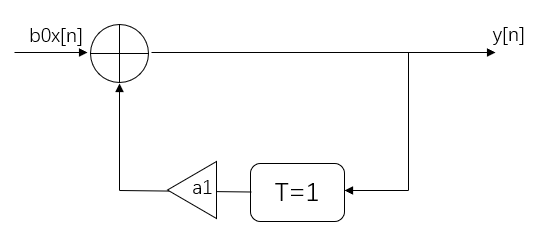
同样的，系统也可以由输入\(x[n]\)与单位脉冲响应\(h[n]\)的卷积来描述：
两边取\(Z\)变换
其中\(H(z) = \frac{Y(z)}{X(z)}\)定义为系统函数，滤波器就是一种系统，也是由系统函数来刻画的。
- 滤波器当前的输出依赖于输入和过去的输出，如\((19)\)，称为无限长单位脉冲响应滤波器（IIR）。
- 滤波器当前的输出仅依赖于输入，而不依赖过去的输出，比如\((19)\)中\(a_i = 0\)的情况，称为有限长单位脉冲响应滤波器（FIR）。
于是IIR数字滤波器可用\((19)\)的差分方程描述。其中\(b_i\)和\(a_i\)决定了每个输入和输出的贡献大小，称为滤波器系数，\(N\)为滤波器阶数。
IIR数字滤波器也可以用系统函数描述，对\((19)\)两边做\(Z\)变换：
推出IIR的系统函数为：
我们一般用计算机辅助设计滤波器时，我们设定好相关参数，结果返回的就是\(b_i\)和\(a_i\)，然后我们再把输入输出经过\((19)\)过程，就完成了滤波。
但如果想知道滤波器系数\(b_i\)和\(a_i\)的具体计算过程的话，建议拿出手边的 《数字信号处理教程》 ，翻到讲解IIR滤波器设计的章节，过程涉及拉氏变换、\(Z\)变换、模拟滤波器映射到数字滤波器双线性变换过程。在百度上是很难搜到计算步骤的，基本没人写这个。如果没书的话可以参考巴特沃斯低通滤波器设计。
如下是用MATLAB辅助设计的步骤，就很容易了：
假设我们需要一个一阶巴特沃斯低通滤波器，N = 1，采样频率Fs=40000Hz，截止频率Fcut = 1000Hz。
令M = 1，根据公式\((19)\)，滤波器的差分方程为：
只要计算出滤波器系数\(b_0\)、\(b_1\)、\(a_1\)，我们就可以直接用差分方程计算滤波器输出结果了，下面是如何使用MATLAB计算它们。
首先在MATLAB中打开Filter Design & Analysis，设置参数如下图，然后在上图标中选择Filter Coefficients，再在Edit中选择Convert to Single Section，然后看到的Numerator对应滤波器系数\(b_i\)，Denominator对应\(a_i\)。滤波系数都有了，接下来该做什么？运行一遍\((22)\)就完事儿了。
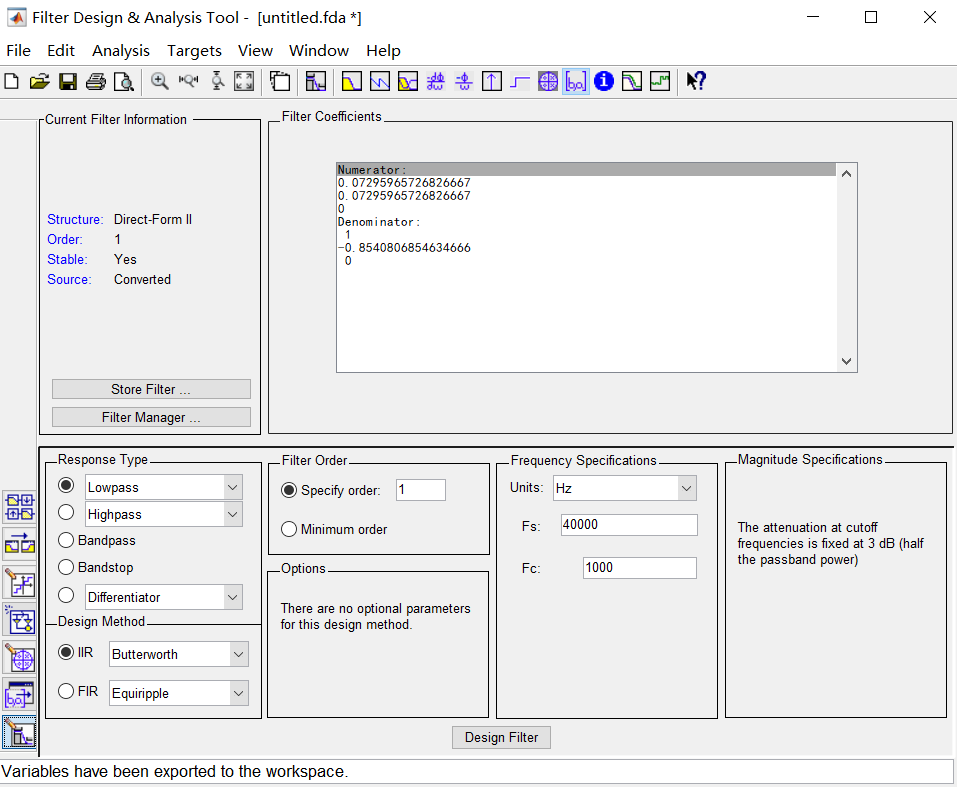
3.4 总结
这是最后的部分输出波形图：
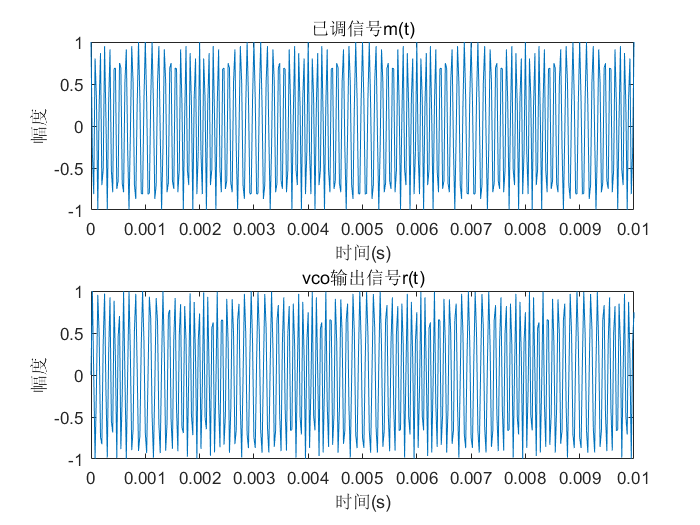
从上图可以看到，VCO对已调信号的跟踪效果还是不错的。
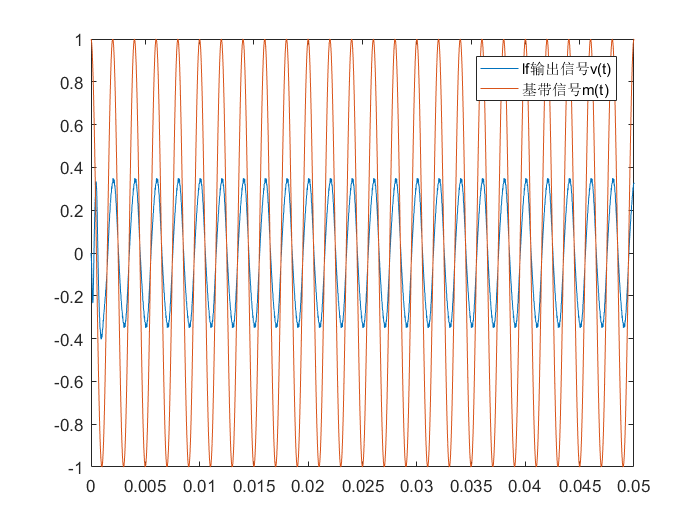
从上图可以看到，锁相环中LF的输出v(t)确实如公式(18)所示，成功恢复了基带信号。
四：完整代码
这里与前面的部分代码相比更改了下采样频率和载波频率以及基带信号频率，还有已调波改成了sin，其余一样。
clc, clear all, close all;
Fs = 40000; % 采样频率
Ts = 1 / Fs;
L = 5000;
t = (0 : L - 1) * Ts;
%% 频率调制(FM)
kf = 2000; % 调频灵敏度
fm = 500; % 基带信号频率
fc = 10000; % 载波频率
mt = cos(2 * pi * fm * t); % 基带信号
st = sin(2 * pi * fc * t + kf * sin(2 * pi * fm * t) / fm); % 由公式(5)写出已调FM信号
% st = sin(2 * pi * fc * t + 2 * pi * kf * cumsum(mt) * Ts); % 也可由公式(4)写出已调FM信号
figure;
subplot(2,1,1)
plot(t,mt); % 观察基带信号时域
title('基带信号时域图'); xlabel('时间(s)'); ylabel('幅度');
subplot(2,1,2)
plot(t,st); % 观察已调信号时域
title('已调信号时域图'); xlabel('时间(s)'); ylabel('幅度');
[ST,f1] = myfft_plot(st,Fs); % 观察已调信号st的频谱
figure;
plot(f1,abs(ST));
title('已调信号频谱图'); xlabel('频率(Hz)'); ylabel('幅度');
%% 非相干解调(包络检波法)
sdt = [0 diff(st)]; % 先对已调信号做微分,公式(6)
rt = abs(hilbert(sdt)); % 再构造解析信号求包络,得到非相干解调信号，公式(11)
% test = 2 * pi * fc + kf .* mt .\ 2000;
figure;
subplot(2,1,1);
plot(t,sdt,t,rt,'r');
legend('微分信号','信号包络');
title('已调信号微分后时域图'); xlabel('时间(s)'); ylabel('幅度');
subplot(2,1,2)
plot(t,mt,'r'); % 观察已调信号时域
title('基带信号时域图'); xlabel('时间(s)'); ylabel('幅度');
figure;
[RT3,f4] = myfft_plot(sdt,Fs); % 观察微分信号频谱
subplot(2,1,1);
plot(f4,abs(RT3));
title('微分信号Sd(t)频谱图'); xlabel('频率(Hz)'); ylabel('幅度');
[RT4,f5] = myfft_plot(hilbert(sdt),Fs); % 观察微分信号单边频谱
subplot(2,1,2);
plot(f5,abs(RT4));
title('微分信号Sd(t)单边频谱图'); xlabel('频率(Hz)'); ylabel('幅度');
[RT,f2] = myfft_plot(rt,Fs); % 观察解调信号频谱
figure;
plot(f2,abs(RT));
title('解调信号频谱图'); xlabel('频率(Hz)'); ylabel('幅度');
figure;
subplot(2,1,1);
plot(t,rt); % 观察解调信号与基带信号
title('解调信号'); xlabel('时间(s)'); ylabel('幅度');
subplot(2,1,2);
plot(t,mt);
title('基带信号'); xlabel('时间(s)'); ylabel('幅度');
%% 相干解调法(同步解调)
% 用锁相环同步
vco_phase = zeros(1,L); % 初始化vco相位
rt = zeros(1,L); % 初始化压控振荡器vco输出
et = zeros(1,L); % 初始化乘法鉴相器pd输出
vt = zeros(1,L); % 初始化环路滤波器lf输出
Av = 1; % vco输出幅度
kv = 40000; % vco频率灵敏度（）
km = 1; % pd增益
k0 = 1; % lf增益
rt(1) = Av * cos(vco_phase(1)); % vco第一次输出
et(1) = km * rt(1) * st(1); % pd第一次输出
b0 = 0.07295965726826667; % Fs = 40000，fcut = 1000的1阶巴特沃斯低通滤波器系数，由FDA生成
b1 = 0.07295965726826667;
a1 = -0.8540806854634666;
vt(1) = k0 * (b0 * et(1)); % 由数字滤波器的差分方程计算lf第一次输出，式(22)
for n = 2 : L; % 不断计算vco的下一次输出相位，最终会跟踪已调信号的相位
vco_phase_change = 2 * pi * fc * Ts + kv * vt(n - 1) * Ts;
vco_phase(n) = vco_phase(n - 1) + vco_phase_change;
rt(n) = Av * cos(vco_phase(n)); % vco输出（会跟踪st的相位）
et(n) = km * rt(n) * st(n); % 乘法鉴相器输出，式(16)
vt(n) = k0 * (b0 * et(n) + b1 * et(n - 1) - a1 * vt(n - 1));% 由数字滤波器的差分方程计算lf输出，式(22)
end
figure;
subplot(2,1,1);
plot(t,st);
title('已调信号m(t)'); xlabel('时间(s)'); ylabel('幅度'); xlim([0 0.01]);
subplot(2,1,2);
plot(t,rt); % 观察vco输出信号与已调信号
title('vco输出信号r(t)'); xlabel('时间(s)'); ylabel('幅度'); xlim([0 0.01]);
figure
plot(t,vt,t,mt)
legend('lf输出信号v(t)','基带信号m(t)');
xlim([0 0.05]);
添加一段myfft_plot函数的代码如下：
%----------------------------------------------------
%介绍:计算信号的双边幅度频谱和其横坐标、并调整使得横坐标中心频率为0Hz
%
%输入：x 输入信号
% Fs 采样频率
%
%输出：X 输入信号的幅度频谱（经过fftshift的）
% freq 输入信号幅度频谱的横坐标
%----------------------------------------------------
function [X,freq]=myfft_plot(x,Fs)
N=length(x);
% 这部分计算频谱的横坐标，使得中心频率为0Hz
if mod(N,2)==0
k=-N/2:N/2-1; % N为偶数
else
k=-(N-1)/2:(N-1)/2; % N为奇数
end
T=N/Fs;
freq=k/T; % 频谱的横坐标
% takes the fft of the signal, and adjusts the amplitude accordingly
X=fft(x)/N; % fft并归一化
X=fftshift(X); % shifts the fft data so that it is centered
五: 参考文献
[1] 吴茂. MATLAB R2016a 通信系统建模与仿真 28 个案例分析. 清华大学出版社, 2018.
