二叉树和二叉查找树 代码分析

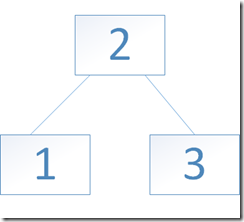
在计算机科学中，二叉树是每个结点最多有两个子树的有序树。（http://baike.baidu.com/view/88806.htm）

二叉树的数据结构：

class Node declaration:

internal class Node
    {
        public int Data { get; set; }
        public Node Left { get; set; }
        public Node Right { get; set; }
    }

二叉树的基本操作:

Interface IBinarySearch declaration:

interface IBinarySearchTree
    {
        void Insert(int i);

        int? FindMin();
        int? FindMax();
        Node Find(int key);

        void PreOrder(Node node);
        void InOrder(Node node);
        void PostOrder(Node node);

        bool Delete(int key);
    }

二叉树方法源代码分析:

二叉树为有序树特点，如图所示，1(left) < 2(parent) < 3(right)。

插入方法：用于构造二叉树。

public void Insert(int key)
        {
            //  创建新结点
              Node newNode = new Node() { Data = key, Left = null, Right = null };
            //  二叉树为空，则新结点为根结点
              if (Root == null)
            {
                Root = newNode;
            }
            else   //  二叉树非空
              {
                Node current = Root;
                Node parent;

                while (true)
                {
                    parent = current;

                    if (current.Data < key)  //  向右子树遍历
                       {
                        current = current.Right;
                        if (current == null)  //  找到目标结点，插入，跳出循环
                            {
                            parent.Right = newNode;
                            break;
                        }
                    }
                    else  // 向左子树遍历
                       {
                        current = current.Left;
                        if (current == null)  //  找到目标结点，插入，跳出循环
                            {
                            parent.Left = newNode;
                            break;
                        }
                    }
                }
            }
        }

找最小值：因为left < parent ,所以只需要从Root结点向左子结点遍历

public int? FindMin()
        {
            //  树为空时返回null
            if (Root == null)
            {
                return null;
            }
            //  树为非空，返回int
            Node current = Root;
            while (current.Left != null)
            {
                current = current.Left;
            }
            return current.Data;
        }

找最大值：因为lparent < right,所以只需要从Root结点向右子结点遍历

public int? FindMax()
        {
            //  树为空时返回null
            if (Root == null)
            {
                return null;
            }
            //  树为非空，返回int
            Node current = Root;
            while (current.Right != null)
            {
                current = current.Right;
            }
            return current.Data;
        }

查找结点：从根结点开始，根据Data与Key的比较
1.Data< key ,遍历右子树
2.Data>key，遍历左子树
3.Data==Key，找到值为key的结点，返回

public Node Find(int key)
        {
            Node current = Root;
            while (true)
            {
                if (current == null)
                {
                    return null;  //  未找到结点
                   }

                if (key < current.Data)  //  遍历左子树
                   {
                    current = current.Left;
                }
                else if (key > current.Data) //  遍历右子树
                   {
                    current = current.Right;
                }
                else  //  找到结点
                   {
                    return current;
                }
            }
        }

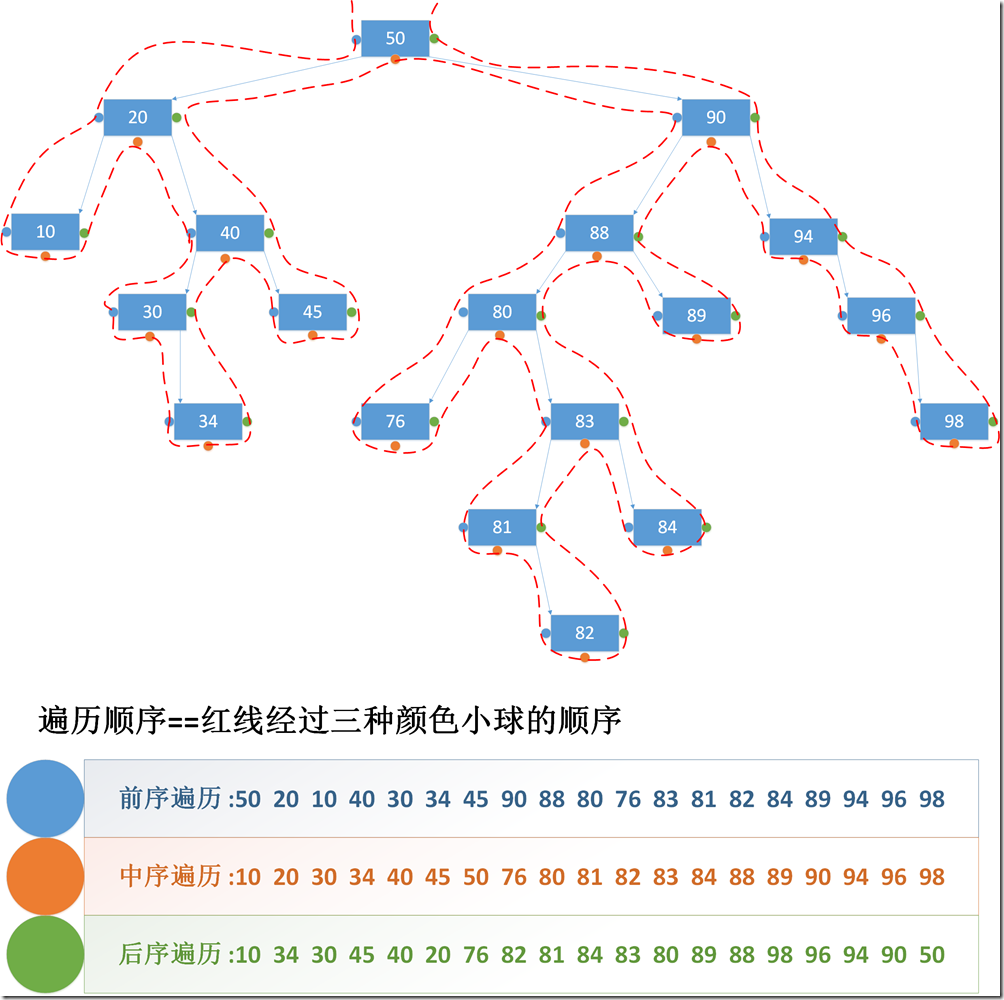
先序遍历：首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树，如果二叉树为空则返回。采用递归的思想。

public void PreOrder(Node node)
       {
            if (node != null)
            {
              Debug.Write(node.Data.ToString() + "  "); //  访问当前结点
                PreOrder(node.Left);   //  遍历左子树
                PreOrder(node.Right);  //  遍历右子树
            }
       }

中序遍历：首先遍历左子树，然后访问根结点，最后遍历右子树。在遍历左、右子树时，仍然先遍历左子树，再访问根结点，最后遍历右子树。采用递归的思想。

public void InOrder(Node node)
       {
            if (node != null)
            {
              InOrder(node.Left);    //  遍历左子树
                Debug.Write(node.Data.ToString() + "  ");   //  访问当前结点
                InOrder(node.Right);   //  遍历右子树
              }
       }

后序遍历：在访问根结点、遍历左子树与遍历右子树三者中，首先遍历左子树，然后遍历右子树，最后遍历访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。采用递归的思想。

public void PostOrder(Node node)
        {
            if (node != null)
            {
              PostOrder(node.Left);  //  遍历左子树
                PostOrder(node.Right); //  遍历右子树 
                Debug.Write(node.Data.ToString() + "  "); //  访问当前结点
              }
        }

删除结点:如果结点存在，则删除，返回true；否则返回false；

结点表示方法:

 
删除结点分为多种情况,下面逐一讨论：
1.二叉树为空树，返回false

if (Root == null)  //  二叉树为空
            {
              return false;
          }

2.未找到该结点，返回false

if (current == null)
                {
                    return false;  //  未找到值为key的结点
                   }

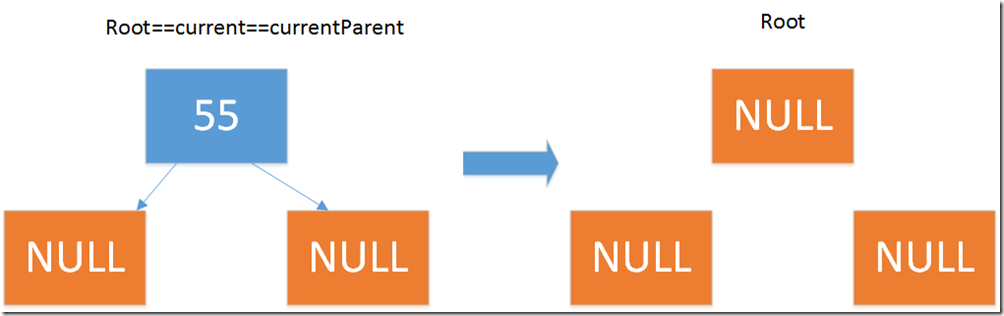
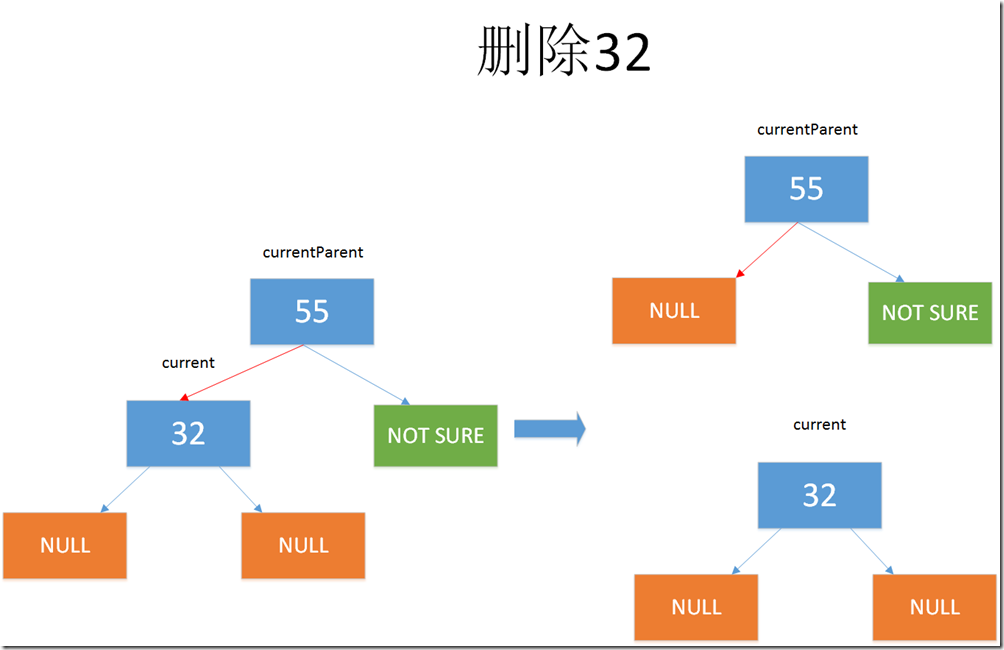
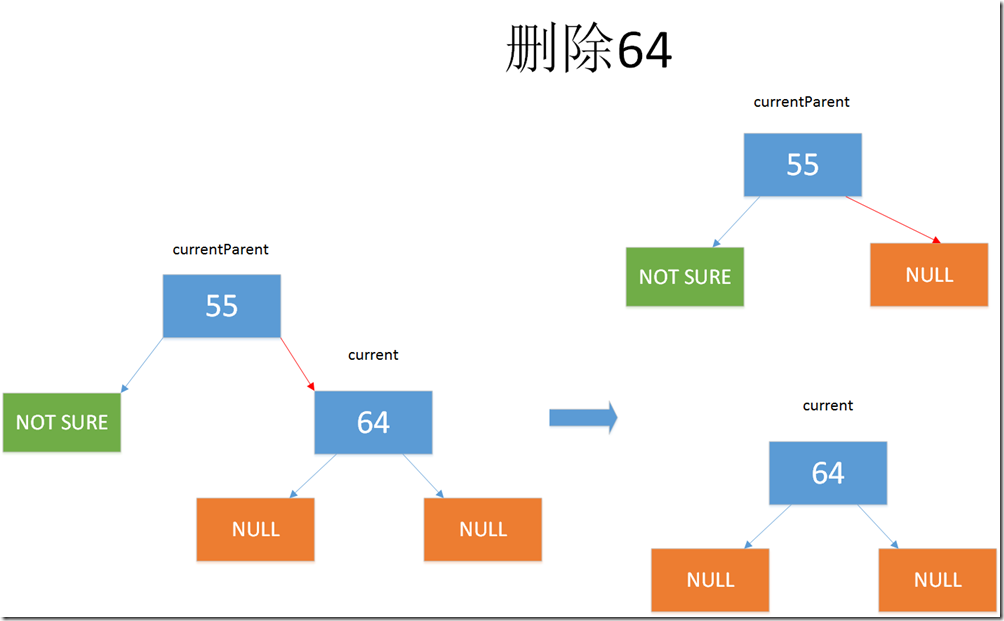
3.删除叶子结点（没有子树）

if (current.Left == null && current.Right == null)
           {
                /*
                 * 注意：
                    * current.Left == null
                 * current.Right == null
                 */
                if (current == Root)
                {
                    Root = null; // 情况一
                }
                else
                {
                    if (isLeft)
                    {
                        currentParent.Left = null; //情况二
                    }
                    else
                    {
                        currentParent.Right = null; //情况三
                    }
                }
            }

情况一：条件current==Root，此时删除值为55的结点，并且Root指向NULL

情况二：条件current!=Root && isLeft==true，此时需要删除current结点,currentParent.Left指向NULL

情况三：条件current!=Root && isLeft==false，此时需要删除current结点,currentParent.Right指向NULL

 
4.删除仅有左子树的结点(一棵子树)

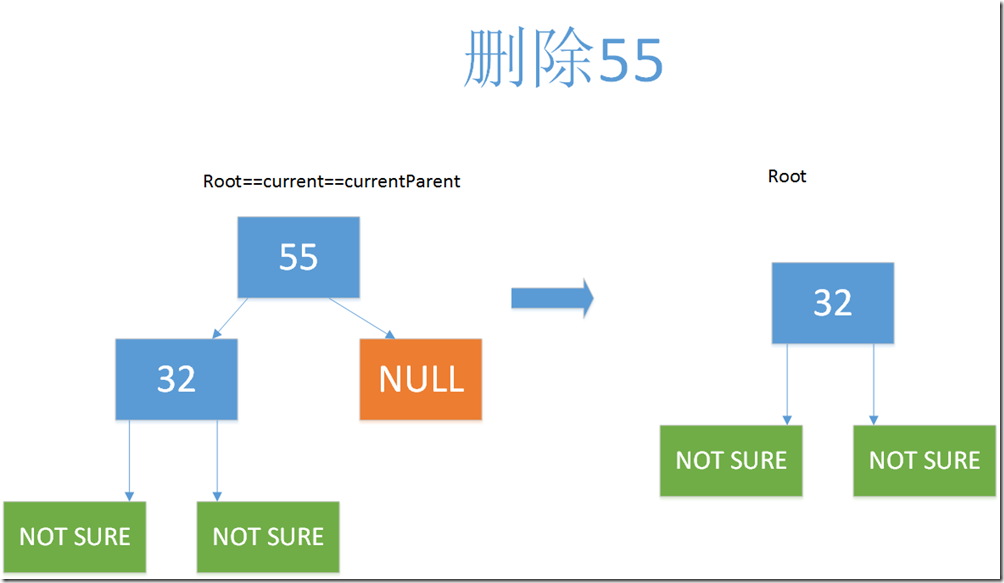
else if (current.Left != null && current.Right == null)
            {
                /*
                 * 注意：
                    * current.Left != null
                 * current.Right == null
                 */
                if (current == Root)
                {
                    Root = current.Left;// 情况一 
                }
                else
                {
                    if (isLeft)
                    {
                        currentParent.Left = current.Left;//情况二 
                    }
                    else
                    {
                        currentParent.Right = current.Left;//情况三
                    }
                }
            }

情况一：条件current==Root ，将Root指向Root.Left

情况二：条件current!=Root && isLeft==true，将currentParent.Left指向current.Left

情况三：条件current!=Root && isLeft==false，将currentParent.Right指向current.Left

5.删除仅有右子树的结点(一棵子树)参考4
6.删除含有左右子树的结点(两棵子树)

 

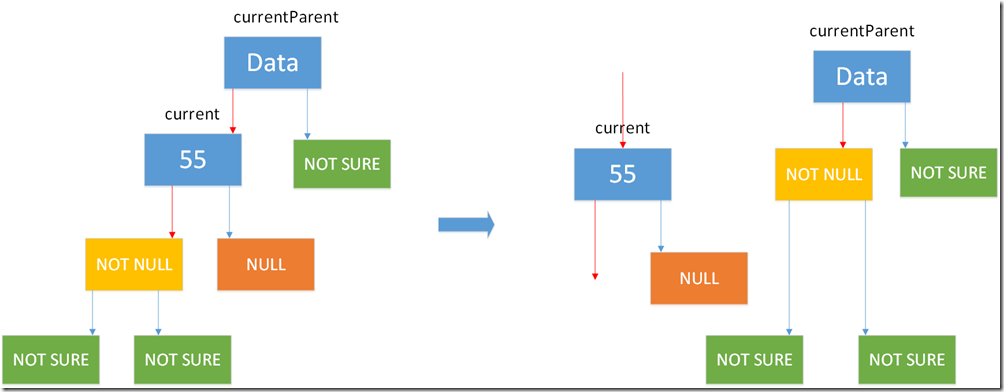
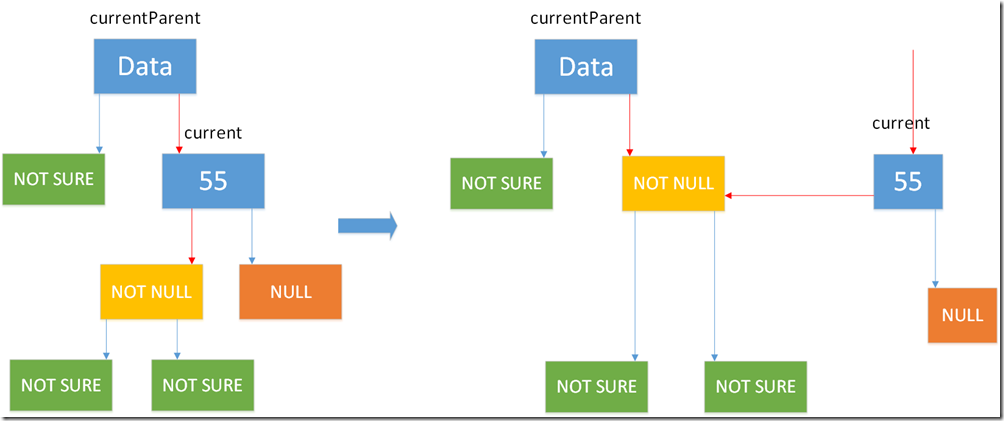
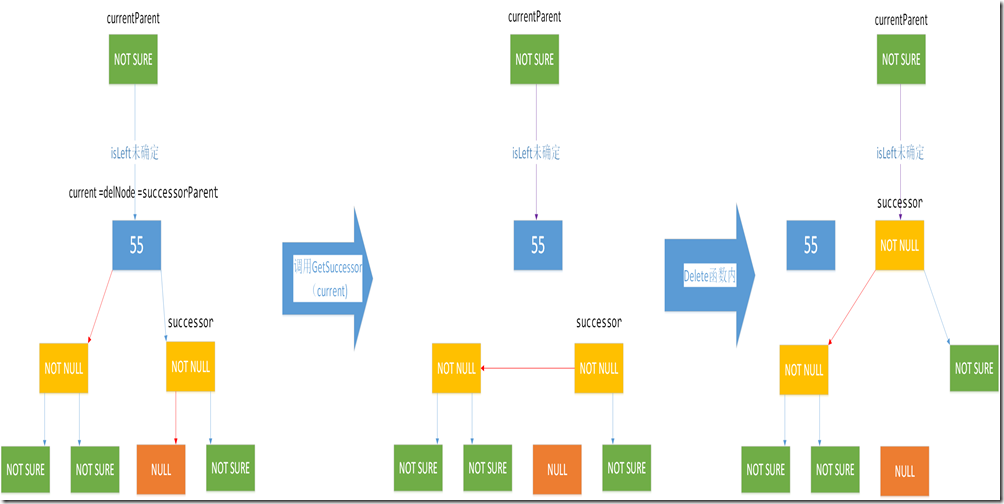
/// <summary>
        /// 获取删除结点的后继结点
        /// 调整后继结点的左右子树
        /// </summary>
        /// <param name="delNode"></param>
        /// <returns></returns>
        private Node GetSuccessor(Node delNode)
        {
            Node successorParent = delNode; //  后继结点的父结点
              Node successor = null;          //  后继结点
              Node current = delNode.Right;   //  current 此时非空
              while (current.Left != null)
            {
                successorParent = current;
                current = current.Left;
                if (current != null && current.Left == null)
                {
                    break;//  找到delNode右子树的后继结点，跳出循环
                   }
            }
            if (successorParent == delNode)   //  delNode.Right 是后继结点，即del.Right.Left=null
            {
                successor = successorParent.Right;
                successor.Left = successorParent.Left;
            }
            else
            {
                successor = successorParent.Left;
                successorParent.Left = successor.Right;
                successor.Right = delNode.Right;
                successor.Left = delNode.Left;
            }
            return successor;
        }

若successosParent == delNode,即“后继结点是要删除结点的右子结点”，如下图过程“调用GetSuccessor(current)”红线所示，找到successor结点(delNode中序遍历的后继结点),调整delNode 左右子树的结构，使其符合构成二叉树的条件：left<parent<right2.在过程“Delete函数内”中，将根据isLeft的值currentParent指向successor结点（需要注意结点55是否为Root结点）

  若successosParent != delNode,即“后继结点不是要删除结点的右子结点”，1.如下图过程“调用GetSuccessor(current)”红线所示，找到successor结点(delNode中序遍历的后继结点),调整delNode 左右子树的结构，使其符合构成二叉树的条件：left<parent<right 2.在过程“Delete函数内”中，将根据isLeft的值currentParent指向successor结点（需要注意结点55是否为Root结点）

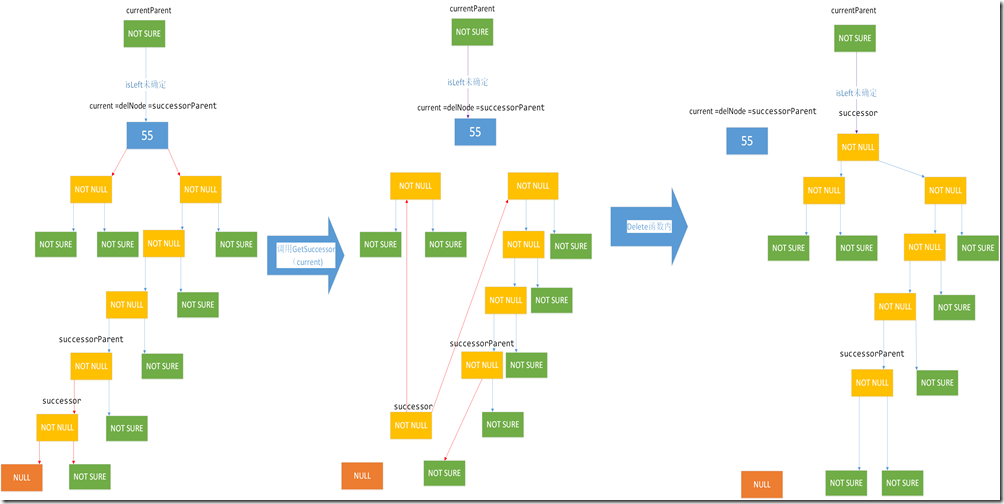
else if (current.Left != null && current.Right != null)
            {
                /*
                 * 注意：
                    * current.Left != null
                 * current.Right != null
                 */
                var successor = GetSuccessor(current);
                if (current == Root)
                {
                    Root = successor;
                }
                else
                {
                    if (isLeft)
                    {
                        currentParent.Left = successor;
                    }
                    else
                    {
                        currentParent.Right = successor;
                    }
                }
            }

Delete方法完整源码：

public bool Delete(int key)
        {
            if (Root == null)  //  二叉树为空
              {
                return false;
            }
            /*
             *  注意：
               *  Root != null
             */
            Node currentParent = Root;
            Node current = Root;
            bool isLeft = true;  //  表示current结点时候为currentParent的左子结点
              while (current.Data != key)
            {
                currentParent = current;
                if (key < current.Data)
                {
                    isLeft = true;  // current结点为currentParent的左子结点
                       current = current.Left;
                }
                else if (key > current.Data)
                {
                    isLeft = false; // current结点为currentParent的右子结点
                       current = current.Right;
                }
                if (current == null)
                {
                    return false;  //  未找到值为key的结点
                   }
            }

            if (current.Left == null && current.Right == null)
            {
                /*
                 * 注意：
                    * current.Left == null
                 * current.Right == null
                 */
                if (current == Root)
                {
                    Root = null;
                }
                else
                {
                    if (isLeft)
                    {
                        currentParent.Left = null;
                    }
                    else
                    {
                        currentParent.Right = null;
                    }
                }
            }
            else if (current.Left != null && current.Right == null)
            {
                /*
                 * 注意：
                    * current.Left != null
                 * current.Right == null
                 */
                if (current == Root)
                {
                    Root = current.Left;
                }
                else
                {
                    if (isLeft)
                    {
                        currentParent.Left = current.Left;
                    }
                    else
                    {
                        currentParent.Right = current.Left;
                    }
                }
            }
            else if (current.Left == null && current.Right != null)
            {
                /*
                 * 注意：
                    * current.Left == null
                 * current.Right != null
                 */
                if (current == Root)
                {
                    Root = current.Right;
                }
                else
                {
                    if (isLeft)
                    {
                        currentParent.Left = current.Right;
                    }
                    else
                    {
                        currentParent.Right = current.Right;
                    }
                }
            }
            else if (current.Left != null && current.Right != null)
            {
                /*
                 * 注意：
                    * current.Left != null
                 * current.Right != null
                 */
                var successor = GetSuccessor(current);
                if (current == Root)
                {
                    Root = successor;
                }
                else
                {
                    if (isLeft)
                    {
                        currentParent.Left = successor;
                    }
                    else
                    {
                        currentParent.Right = successor;
                    }
                }
            }
            return true;
        }

二叉树的UnitTest:

Initialize()方法构造二叉树，具体测试内容见TestAll()方法的注释。</>

    [TestClass]
    public class BinarySearchTree_Test
    {
        private BinarySearchTree _tree = new BinarySearchTree();

        [TestInitialize]
        public void Initialize()
        {
            DebugMessage.WriteLineMsg("Initialize() Start :\\n");

            StringBuilder builder = new StringBuilder();
            //var items = RandomProducer(10);
            //items.Add(30);
            //items.Add(40);
            //items.Add(50);
            //items.Add(60);

            var items = new List<int> { 50, 20, 90, 10, 40, 88, 94, 30, 45, 80, 89, 96, 34, 76, 83, 98, 81, 84, 82 };

            builder.Append("The List is :");
            foreach (var item in items)
            {
                Insert_Test(item);

                builder.Append(item + "   ");
            }
            DebugMessage.WriteLineMsg(builder.ToString());
            ShowTree();
        }

        /// <summary>
        /// 在50, 20, 90, 10, 40, 88, 94, 30, 45, 80, 89, 96, 34, 76, 83, 98, 81, 84, 82构成的二叉树中
        /// 查找最小值，最大值
        /// 
        /// 查询50，80，1000
        /// 
        /// 先序遍历，中序遍历，后序遍历
        /// 
        /// 删除10(不包含子树)
        /// 删除30(仅包含右子树)
        /// 删除80(包含左右子树)
        /// 删除90(包含左右子树)
        /// </summary>
        [TestMethod]
        public void TestAll()
        {
            FindMin_Test();
            FindMax_Test();

            Find_Test(50);
            Find_Test(80);
            Find_Test(1000);

            PreOrder_Test();
            InOrder_Test();
            PostOrder_Test();

            Debug.WriteLine("\n\n");

            Delete_Test(10);
            Delete_Test(30);
            Delete_Test(80);
            Delete_Test(90);
        }

        [TestMethod]
        public void Insert_Test(int key)
        {
            _tree.Insert(key);
        }

        [TestMethod]
        public void FindMin_Test()
        {
            var min = _tree.FindMin();
            DebugMessage.WriteLineIfMsg(min != null, String.Format("Min : {0}", min.Value));
        }
        [TestMethod]
        public void FindMax_Test()
        {
            var max = _tree.FindMax();
            DebugMessage.WriteLineIfMsg(max != null, String.Format("Max : {0}", max.Value));
        }

        [TestMethod]
        public void Find_Test(int key)
        {
            var node = _tree.Find(key);
            DebugMessage.WriteLineMsg(node == null ? String.Format("Can't find {0} in the tree", key) : String.Format("Find {0} in the tree", key));
        }

        [TestMethod]
        public void PreOrder_Test()
        {
            DebugMessage.WriteMsg("\nPreOrder :");
            _tree.PreOrder(_tree.Root);
        }

        [TestMethod]
        public void InOrder_Test()
        {
            DebugMessage.WriteMsg("\nInOrder :");
            _tree.InOrder(_tree.Root);
        }

        [TestMethod]
        public void PostOrder_Test()
        {
            DebugMessage.WriteMsg("\nPostOrder :");
            _tree.PostOrder(_tree.Root);
        }
        [TestMethod]
        public void Delete_Test(int key)
        {
            DebugMessage.WriteLineMsg("Delete " + key);
            _tree.Delete(key);
            ShowTree();
        }

        /// <summary>
        /// 遍历输出二叉树结构
        /// </summary>
        private void ShowTree()
        {
            if (_tree.Root == null)
            {
                return;
            }
            DebugMessage.WriteLineMsg("\nRoot :" + _tree.Root.Data.ToString());
            Show(_tree.Root);
            DebugMessage.WriteEndMsg();
        }
        private void Show(Node current)
        {
            if (current == null)
            {
                return;
            }
            StringBuilder builder = new StringBuilder();
            builder.Append("Parent : " + current.Data + "    ");
            if (current.Left != null)
            {
                builder.Append("Left : " + current.Left.Data + "    ");
            }
            if (current.Right != null)
            {
                builder.Append("Right : " + current.Right.Data + "    ");
            }
            DebugMessage.WriteLineMsg(builder.ToString());

            if (current.Left != null)
            {
                Show(current.Left);
            }
            if (current.Right != null)
            {
                Show(current.Right);
            }
        }
        /// <summary>
        /// 产生counter个随机数
        /// </summary>
        /// <param name="counter"></param>
        /// <returns></returns>
        private IList<int> RandomProducer(int counter)
        {
            var lists = new List<int>();
            Random rnd = new Random(Guid.NewGuid().GetHashCode());
            for (int index = 0; index < counter; index++)
            {
                int item = rnd.Next(0, 100);
                lists.Add(item);
            }
            return lists;
        }
    }

测试结果：</>

Initialize() Start :\n
The List is :50   20   90   10   40   88   94   30   45   80   89   96   34   76   83   98   81   84   82   

Root :50
Parent : 50    Left : 20    Right : 90    
Parent : 20    Left : 10    Right : 40    
Parent : 10    
Parent : 40    Left : 30    Right : 45    
Parent : 30    Right : 34    
Parent : 34    
Parent : 45    
Parent : 90    Left : 88    Right : 94    
Parent : 88    Left : 80    Right : 89    
Parent : 80    Left : 76    Right : 83    
Parent : 76    
Parent : 83    Left : 81    Right : 84    
Parent : 81    Right : 82    
Parent : 82    
Parent : 84    
Parent : 89    
Parent : 94    Right : 96    
Parent : 96    Right : 98    
Parent : 98    

*********

Min : 10
Max : 98
Find 50 in the tree
Find 80 in the tree
Can't find 1000 in the tree

PreOrder :50  20  10  40  30  34  45  90  88  80  76  83  81  82  84  89  94  96  98  
InOrder :10  20  30  34  40  45  50  76  80  81  82  83  84  88  89  90  94  96  98  
PostOrder :10  34  30  45  40  20  76  82  81  84  83  80  89  88  98  96  94  90  50  


Delete 10

Root :50
Parent : 50    Left : 20    Right : 90    
Parent : 20    Right : 40    
Parent : 40    Left : 30    Right : 45    
Parent : 30    Right : 34    
Parent : 34    
Parent : 45    
Parent : 90    Left : 88    Right : 94    
Parent : 88    Left : 80    Right : 89    
Parent : 80    Left : 76    Right : 83    
Parent : 76    
Parent : 83    Left : 81    Right : 84    
Parent : 81    Right : 82    
Parent : 82    
Parent : 84    
Parent : 89    
Parent : 94    Right : 96    
Parent : 96    Right : 98    
Parent : 98    

*********

Delete 30

Root :50
Parent : 50    Left : 20    Right : 90    
Parent : 20    Right : 40    
Parent : 40    Left : 34    Right : 45    
Parent : 34    
Parent : 45    
Parent : 90    Left : 88    Right : 94    
Parent : 88    Left : 80    Right : 89    
Parent : 80    Left : 76    Right : 83    
Parent : 76    
Parent : 83    Left : 81    Right : 84    
Parent : 81    Right : 82    
Parent : 82    
Parent : 84    
Parent : 89    
Parent : 94    Right : 96    
Parent : 96    Right : 98    
Parent : 98    

*********

Delete 80

Root :50
Parent : 50    Left : 20    Right : 90    
Parent : 20    Right : 40    
Parent : 40    Left : 34    Right : 45    
Parent : 34    
Parent : 45    
Parent : 90    Left : 88    Right : 94    
Parent : 88    Left : 81    Right : 89    
Parent : 81    Left : 76    Right : 83    
Parent : 76    
Parent : 83    Left : 82    Right : 84    
Parent : 82    
Parent : 84    
Parent : 89    
Parent : 94    Right : 96    
Parent : 96    Right : 98    
Parent : 98    

*********

Delete 90

Root :50
Parent : 50    Left : 20    Right : 94    
Parent : 20    Right : 40    
Parent : 40    Left : 34    Right : 45    
Parent : 34    
Parent : 45    
Parent : 94    Left : 88    Right : 96    
Parent : 88    Left : 81    Right : 89    
Parent : 81    Left : 76    Right : 83    
Parent : 76    
Parent : 83    Left : 82    Right : 84    
Parent : 82    
Parent : 84    
Parent : 89    
Parent : 96    Right : 98    
Parent : 98    

*********

前序，中序，后序遍历的简便判别方法（以测试代码中构造的二叉树为例）

 

本示例代码下载（[November 10 2012]二叉树和二叉查找树 代码分析.zip）：https://skydrive.live.com/?cid=B53A8D0EF3B97142&id=B53A8D0EF3B97142%21110#cid=B53A8D0EF3B97142&id=B53A8D0EF3B97142%21110