空间距离
1.两点间的距离:即两个点之间的线段的长度。
2.点到直线的距离:点和直线的距离是点到直线的垂直线段的长度
若在平面坐标几何上的直线定义为 ax + by + c = 0,点的座
标为(x0, y0), 则它们之间的距离为
3.异面直线间的距离
设两直线的方程分别为 :
则,该两直线间的距离
4.点到平面的距离
若点坐标为(x0, y0, z0), 平面为Ax + By + Cz + D = 0, 则点到平面的距离为
推广到超平面,若Rn空间中点坐标为x = (x1, x2, ..., xn) ∈ Rn, Rn空间中的超平面可以使用一个系数向量w和平移(偏置)b表示,为<w, b>, 即f(x) = wx + b = 0, f(x) = 0就是Rn空间中的一个超平面。某点与此超平面的距离为
5.两平行直线
若直线分为 ax + by + c1 = 0 和 ax + by + c2 = 0, 则它们之间的距离为
6.两平行平面间的距离
若两平为 Ax + By + Cz + D1 = 0 和 Ax + By + Cz + D2 = 0 则他们之间的距离为
7.范数
设在Rn空间有两点,p = (p1, p2, ..., pn),q = (q1, q2, ..., qn),不同的范数都是一种距离:
无穷大阶范数=t阶范数的极限 ,即n趋向无穷大(无穷范数——向量中最大元素的绝对值)
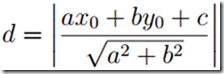
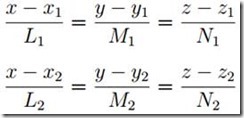
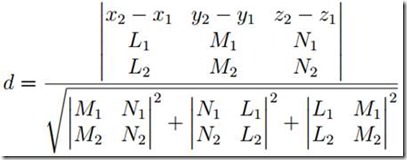
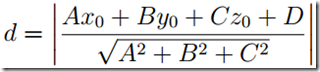
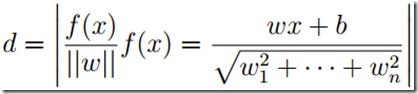
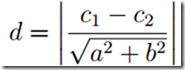
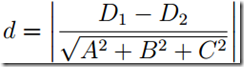

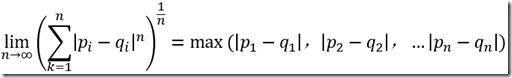

 浙公网安备 33010602011771号
浙公网安备 33010602011771号