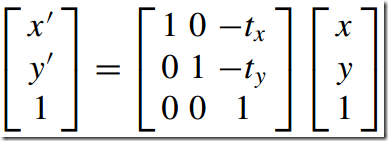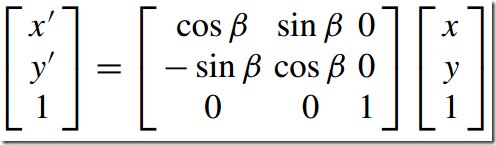坐标轴变换

Four coordinate systems are used in the computer graphics pipeline: object space, world space, camera space and image space

• The object space is a domain where objects are modelled and assembled.
• The world space is where objects are positioned and animated through appropriate transforms. The world space also hosts a virtual camera or observer.
• The camera space is a transform of the world space relative to the camera.
• Finally, the image space is a projection—normally perspective—of the camera space onto an image plane.

1. 二维变换

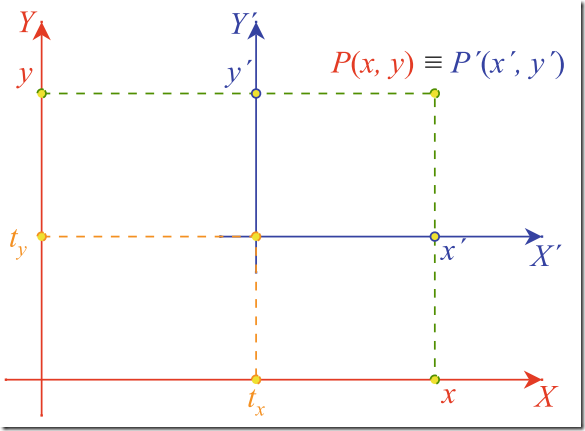
1） 平移—Translation

If the second coordinate system is a simple translation (tx, ty) relative to the reference system

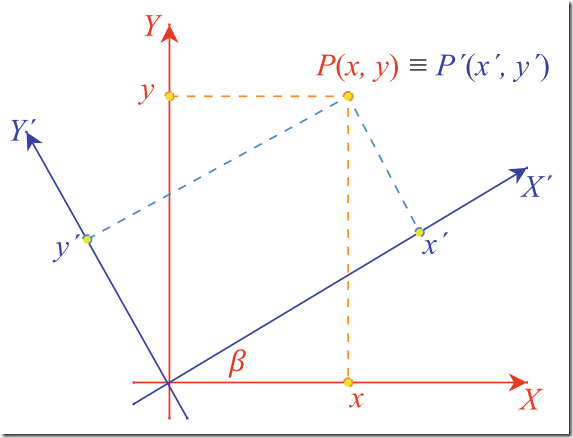
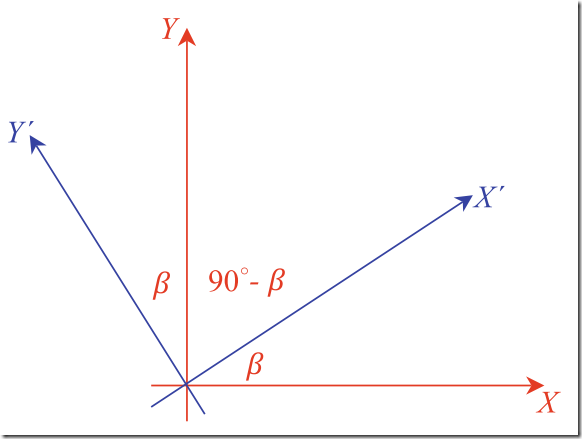
2） 旋转—Rotation

If the X Y -axes are rotated β relative to the XY -axes

3） 旋转与平移

4） 方向余弦—2D Direction Cosines

2. 三维变换

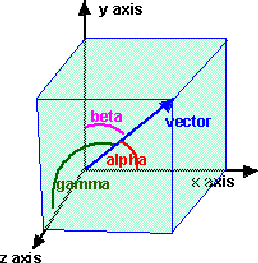
1） 方向余弦—3D Direction Cosines

A 3D vector can be used to define a direction. If a vector is used to define direction in this way then the length of the vector is not relevant, therefore we can use a unit length vector.

So if the vector is: (x,y,z)

where:

• x is the length of the vector in the x dimension.
• y is the length of the vector in the y dimension.
• z is the length of the vector in the z dimension.

So for a normalised vector:

x² + y² + z² = 1

The angles from the vector to the coordinate axes are given by:

• x = cos(alpha)
• y = cos(beta)
• z = cos(gamma)

x,y and z are known as the direction cosines.

The direction cosines are not independent of each other, they are related by the equation x² + y² + z² = 1, so direction cosines only have two degrees of freedom and can only represent direction and not orientation. What this means is that direction cosines do not define how much an object is rotated around the axis of the vector.

---------------------------------------------------------------------------------------------------------------------

2） 欧拉角—Euler Angles