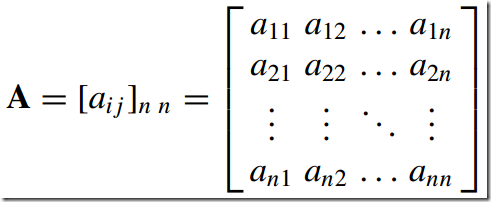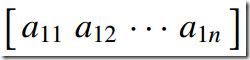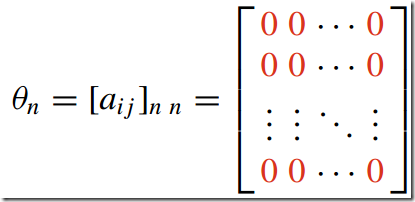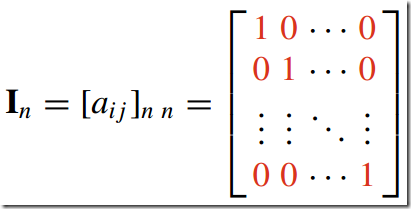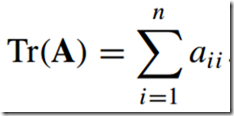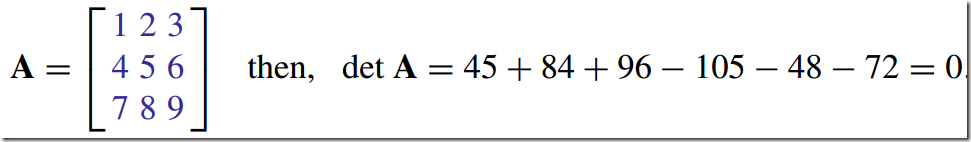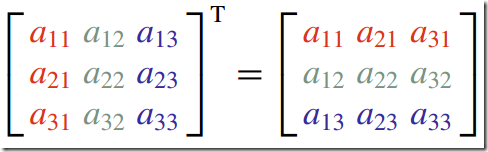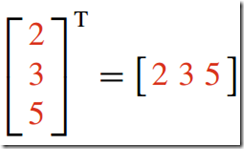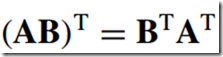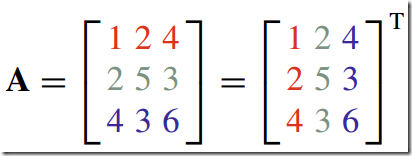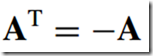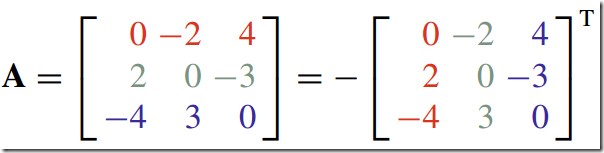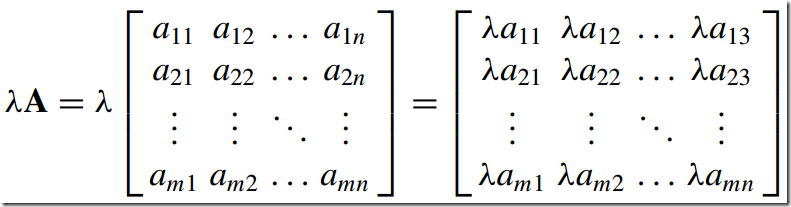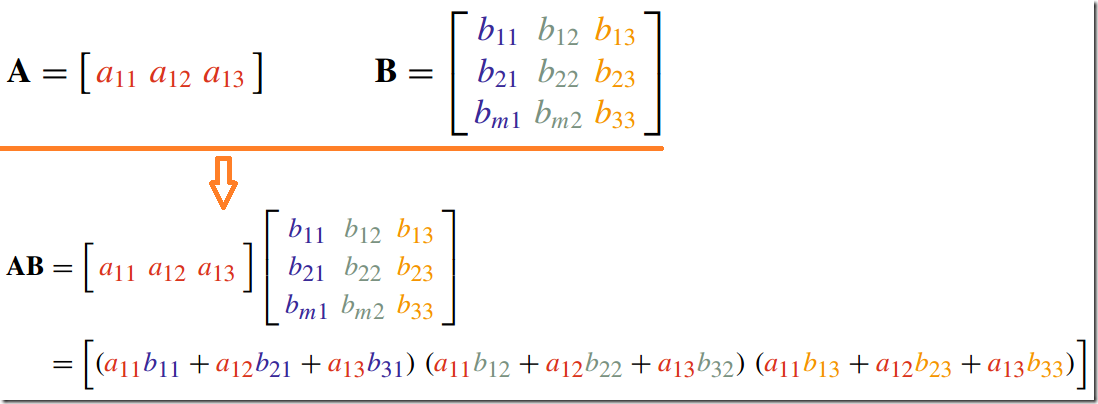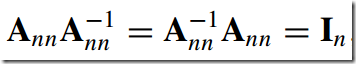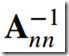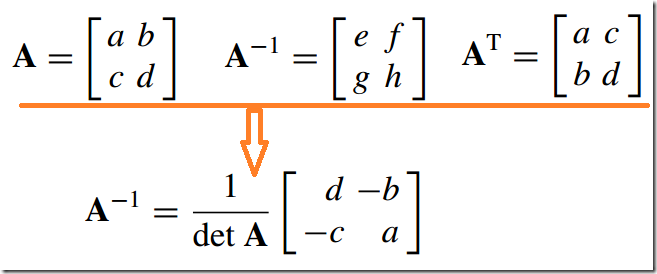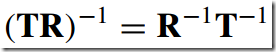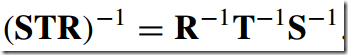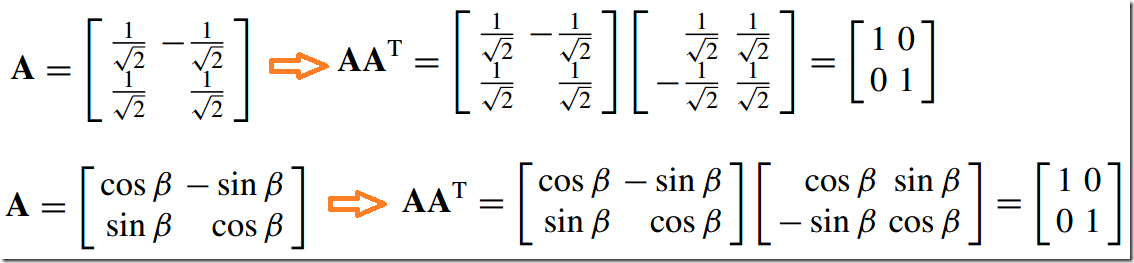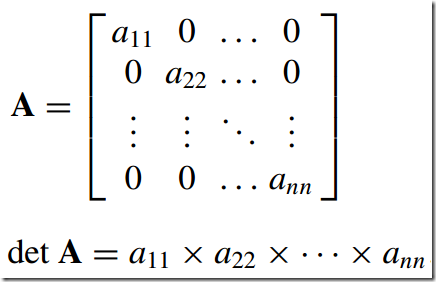矩阵
1. 概念
1)矩阵的维度--Matrix Dimension or Order
The dimension or order of a matrix is the expression m × n where m is the number of rows, and n is the number of columns.
2)方形矩阵--Square Matrix
行与列个数相等的矩阵
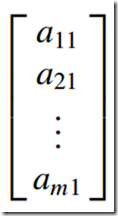
3)列矢量--Column Vector
只有一列元素的矩阵
4)行矢量--Row Vector
只有一行元素的矩阵
4)空矩阵--Null Matrix
所有元素都为0的矩阵
5)单位矩阵--Unit Matrix
所有主对角元素(从a00到ann)都为1,其它元素为0的矩阵
6)方阵的迹--Trace
所有主对角元素(从a00到ann)的和
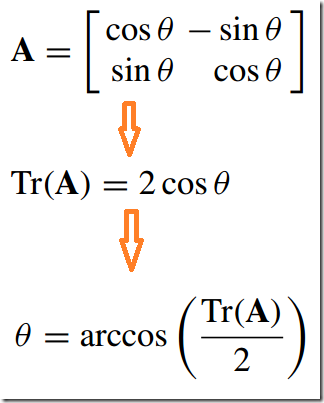
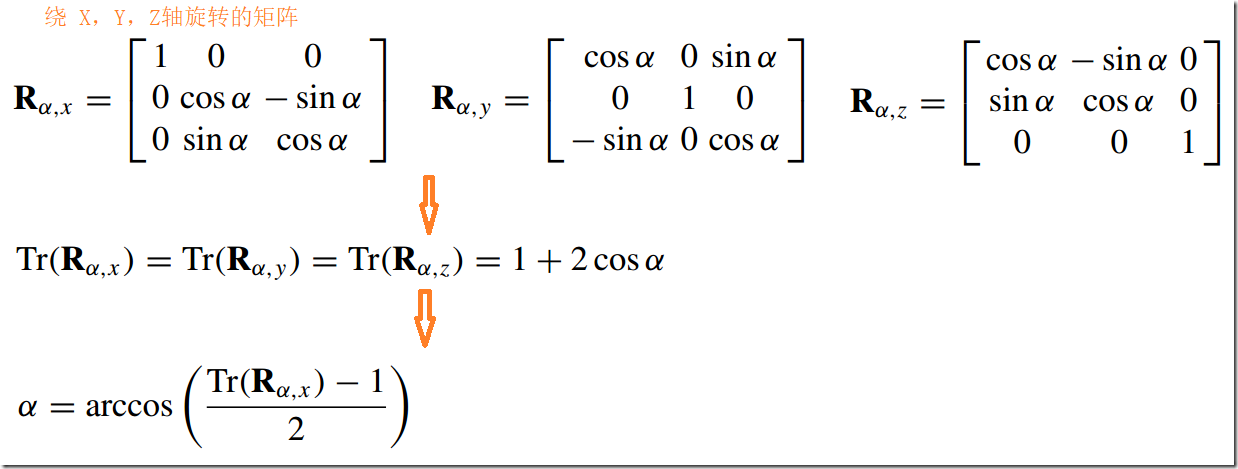
1.可用于计算一点围绕原点的旋转角度
7)方阵的行列式--Determinant of a Matrix
The determinant of a matrix is a scalar value computed from the elements of the matrix
8)转置--Transpose
矩阵行元素与列元素进行交换形成的矩阵
性质:
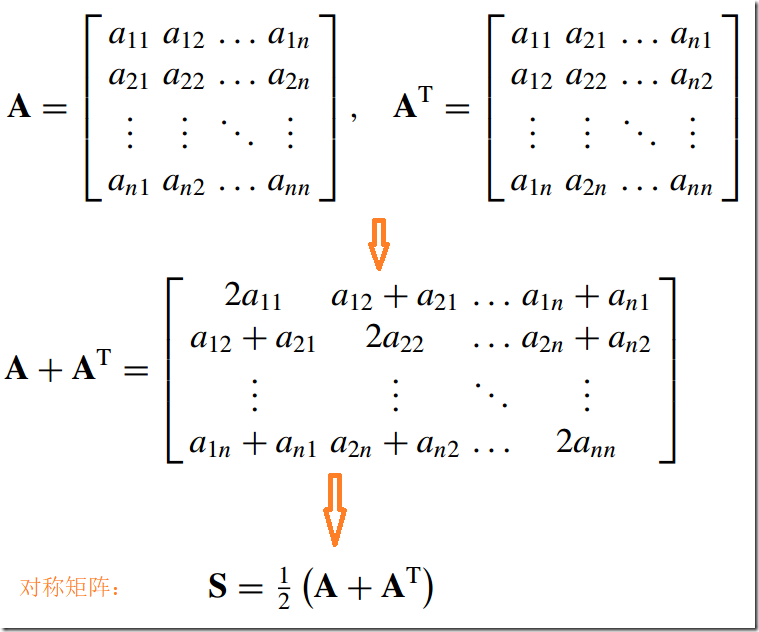
9)对称矩阵--Symmetric Matrix
生成一个对称矩阵
10)反对称矩阵--Antisymmetric Matrix/skew-symmetric matrix
生成一个反对称矩阵
2. 操作
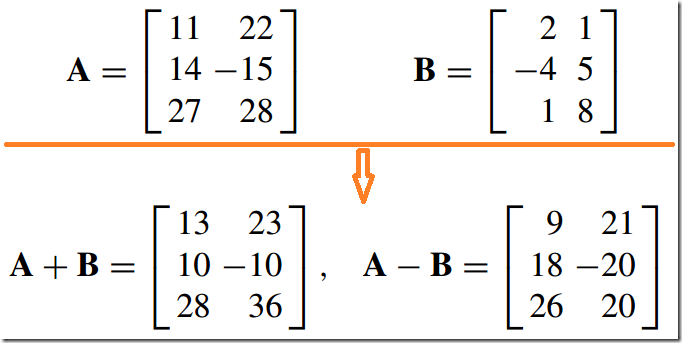
1)加减法--Matrix Addition and Subtraction
对应元素相加/减
2)标量相乘--Scalar Multiplication
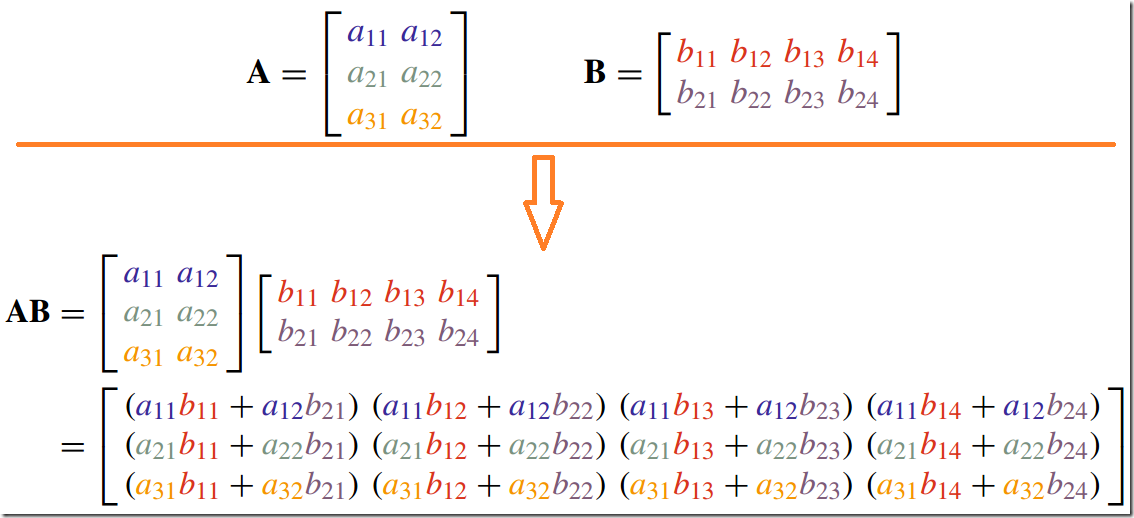
3)矩阵积--Matrix Products
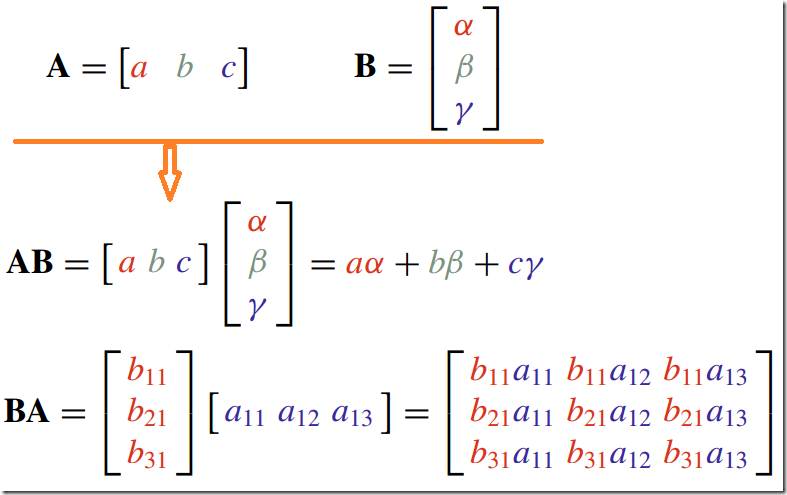
1.行列矢量的乘积--Row and Column Vectors
2.行矢量与矩阵的乘积--Row Vector and a Matrix
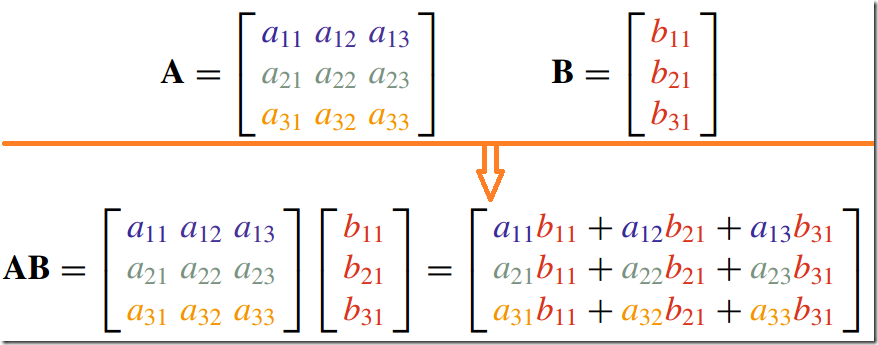
3.矩阵与列矢量的乘积--Matrix and a Column Vector
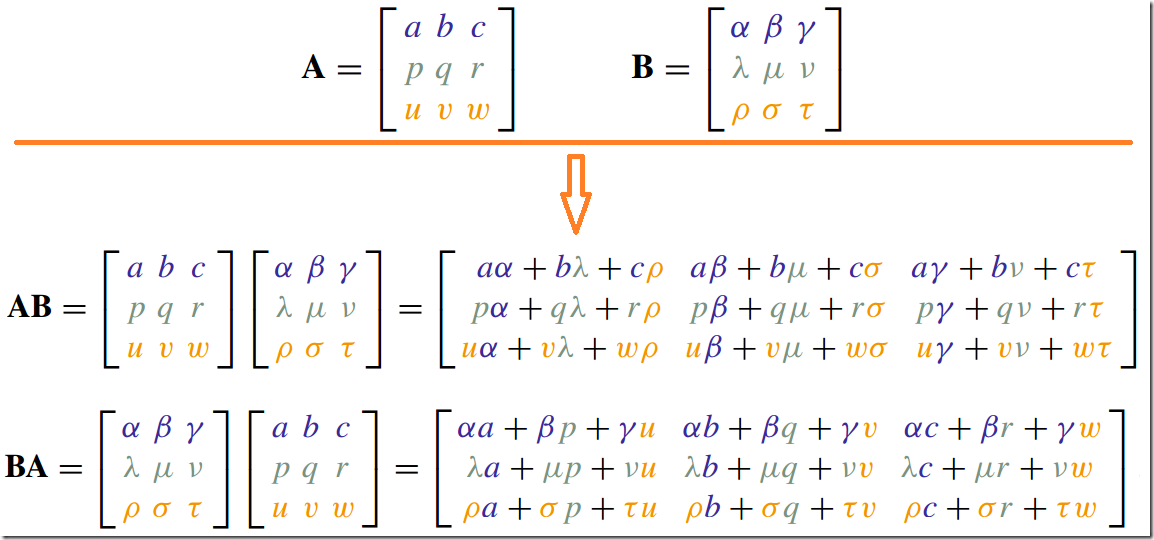
4.方阵乘积--Square Matrices
4)逆矩阵--Inverse Matrix
当一个方阵的行列式的值为0时,它没有逆矩阵,它被称为奇异矩阵(singular matrix)
5)求一对矩阵的逆--Inverting a Pair of Matrices
6)正交矩阵--Orthogonal Matrix
A matrix is orthogonal if its transpose is also its inverse,即 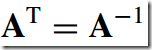
例如:
正交矩阵的作用:Orthogonal matrices play an important role in rotations because they leave the origin fixed and preserve all angles and distances. Consequently, an object’s geometric integrity is maintained after a rotation, which is why an orthogonal transform is known as a rigid motion transform(刚体运动变换)
6)对角矩阵--Diagonal Matrix
除主对角上的元素外,其它元素全为0的矩阵