三维网格细分算法(Catmull-Clark subdivision & Loop subdivision)附源码(转载)
转载: https://www.cnblogs.com/shushen/p/5251070.html
下图描述了细分的基本思想,每次细分都是在每条边上插入一个新的顶点,可以看到随着细分次数的增加,折线逐渐变成一条光滑的曲线。曲面细分需要有几何规则和拓扑规则,几何规则用于计算新顶点的位置,拓扑规则用于确定新顶点的连接关系。下面介绍两种网格细分方法:Catmull-Clark细分和Loop细分。

Catmull-Clark subdivision:
Catmull-Clark细分是一种四边形网格的细分法则,每个面计算生成一个新的顶点,每条边计算生成一个新的顶点,同时每个原始顶点更新位置。下图为Catmull-Clark细分格式的细分掩膜,对于新增加的顶点位置以及原始顶点位置更新规则如下:

1.网格内部F-顶点位置:
设四边形的四个顶点为v0、v1、v2、v3,则新增加的顶点位置为v = 1/4*(v0 + v1 + v2 + v3)。
2.网格内部V-顶点位置:
设内部顶点v0的相邻点为v1、v2,…,v2n,则该顶点更新后位置为![]() ,其中α、β、γ分别为α = 1 - β - γ。
,其中α、β、γ分别为α = 1 - β - γ。
3.网格边界V-顶点位置:
设边界顶点v0的两个相邻点为v1、v2,则该顶点更新后位置为v = 3/4*v0 + 1/8*(v1 + v2)。
4.网格内部E-顶点位置:
设内部边的两个端点为v0、v1,与该边相邻的两个四边形顶点分别为v0、v1、v2、v3和v0、v1、v4、v5,则新增加的顶点位置为v = 1/4*(v0 + v1 + vf1 + vf2) = 3/8*(v0 + v1) + 1/16*(v2 + v3 + v4 + v5)。
5.网格边界E-顶点位置:
设边界边的两个端点为v0、v1,则新增加的顶点位置为v = 1/2*(v0 + v1)。
效果:
function [VV, FF, S] = CC_subdivision(V, F, iter) % Catmull_Clark subdivision if ~exist('iter','var') iter = 1; end VV = V; FF = F; for i = 1:iter nv = size(VV,1); nf = size(FF,1); O = outline(FF); original = 1:nv; boundary = O(:,1)'; interior = original(~ismember(original, boundary)); no = length(original); nb = length(boundary); ni = length(interior); %% Sv Etmp = sort([FF(:,1) FF(:,2);FF(:,2) FF(:,3);FF(:,3) FF(:,4);FF(:,4) FF(:,1)],2); [E, ~, idx] = unique(Etmp, 'rows'); Aeven = sparse([E(:,1) E(:,2)], [E(:,2) E(:,1)], 1, no, no); Aodd = sparse([FF(:,1) FF(:,2)], [FF(:,3) FF(:,4)], 1, no, no); Aodd = Aodd + Aodd'; val_even = sum(Aeven,2); beta = 3./(2*val_even); val_odd = sum(Aodd,2); gamma = 1./(4*val_odd); alpha = 1 - beta - gamma; Sv = sparse(no,no); Sv(interior,:) = ... sparse(1:ni, interior, alpha(interior), ni, no) + ... bsxfun(@times, Aeven(interior,:), beta(interior)./val_even(interior)) + ... bsxfun(@times, Aodd(interior,:), gamma(interior)./val_odd(interior)); Sboundary = ... sparse([O(:,1);O(:,2)],[O(:,2);O(:,1)],1/8,no,no) + ... sparse([O(:,1);O(:,2)],[O(:,1);O(:,2)],3/8,no,no); Sv(boundary,:) = Sboundary(boundary,:); %% Sf Sf = 1/4 .* sparse(repmat((1:nf)',1 ,4), FF, 1); i0 = no + (1:nf)'; %% Se flaps = sparse([idx;idx], ... [FF(:,3) FF(:,4);FF(:,4) FF(:,1);FF(:,1) FF(:,2);FF(:,2) FF(:,3)], ... 1); onboundary = (sum(flaps,2) == 2); flaps(onboundary,:) = 0; ne = size(E,1); Se = sparse( ... [1:ne 1:ne]', ... [E(:,1); E(:,2)], ... [onboundary;onboundary].*1/2 + ~[onboundary;onboundary].*3/8, ... ne, ... no) + ... flaps*1/16; %% new faces & new vertices i1 = no + nf + (1:nf)'; i2 = no + 2*nf + (1:nf)'; i3 = no + 3*nf + (1:nf)'; i4 = no + 4*nf + (1:nf)'; FFtmp = [i0 i4 FF(:,1) i1; ... i0 i1 FF(:,2) i2; ... i0 i2 FF(:,3) i3; ... i0 i3 FF(:,4) i4]; reidx = [(1:no)'; no+(1:nf)'; no+nf+idx]; FF = reidx(FFtmp); S = [Sv; Sf; Se]; VV = S*VV; end end


Loop subdivision:
Loop细分是一种三角形网格的细分法则,它按照1-4三角形分裂,每条边计算生成一个新的顶点,同时每个原始顶点更新位置。下图为Loop细分格式的细分掩膜,对于新增加的顶点位置以及原始顶点位置更新规则如下:

1.网格内部V-顶点位置:
设内部顶点v0的相邻点为v1、v2,…,vn,则该顶点更新后位置为 ,其中
,其中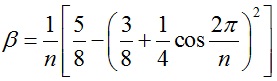 。
。
2.网格边界V-顶点位置:
设边界顶点v0的两个相邻点为v1、v2,则该顶点更新后位置为v = 3/4*v0 + 1/8*(v1 + v2)。
3.网格内部E-顶点位置:
设内部边的两个端点为v0、v1,相对的两个顶点为v2、v3,则新增加的顶点位置为v = 3/8*(v0 + v1) + 1/8*(v2 + v3)。
4.网格边界E-顶点位置:
设边界边的两个端点为v0、v1,则新增加的顶点位置为v = 1/2*(v0 + v1)。
效果:




