Cesium专栏-样条插值(平滑路径、飞行动画,源码下载)
Cesium
Cesium 是一款面向三维地球和地图的,世界级的JavaScript开源产品。它提供了基于JavaScript语言的开发包,方便用户快速搭建一款零插件的虚拟地球Web应用,并在性能,精度,渲染质量以及多平台,易用性上都有高质量的保证。
效果图

关于插值的认识
在Cesium官网中有介绍飞机飞行路线插值的例子,介绍了3中插值的使用方式。
分别是:
LinearApproximation
-
entity.position.setInterpolationOptions({
-
interpolationDegree : 1,
-
interpolationAlgorithm : Cesium.LinearApproximation
-
});
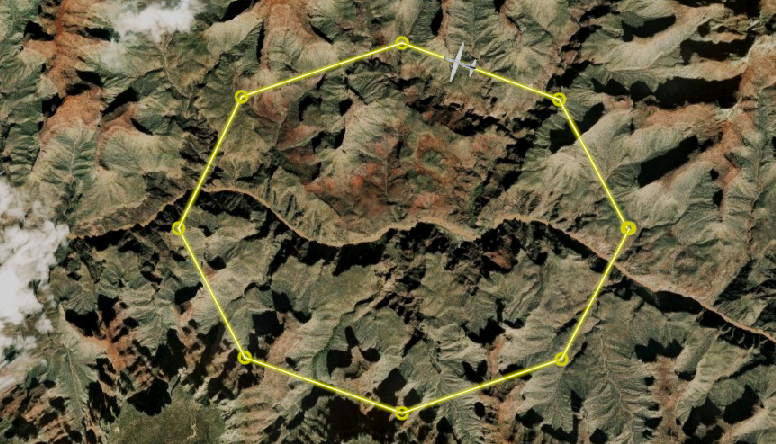 LagrangePolynomialApproximation
LagrangePolynomialApproximation
-
entity.position.setInterpolationOptions({
-
interpolationDegree : 5,
-
interpolationAlgorithm : Cesium.LagrangePolynomialApproximation
-
});
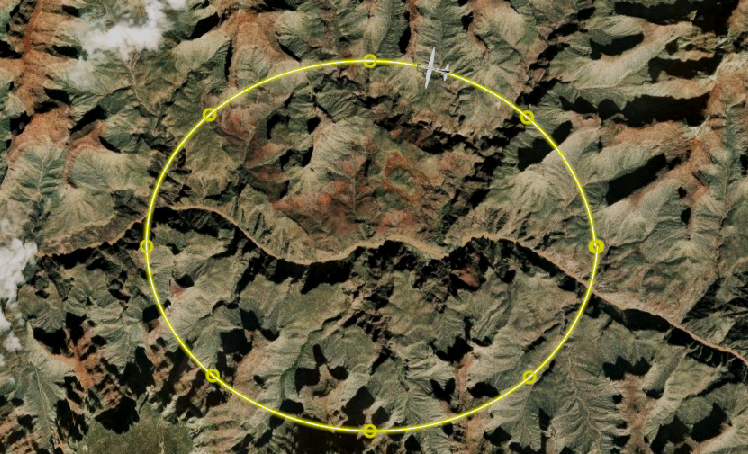 HermitePolynomialApproximation
HermitePolynomialApproximation
-
entity.position.setInterpolationOptions({
-
interpolationDegree : 2,
-
interpolationAlgorithm : Cesium.HermitePolynomialApproximation
-
});
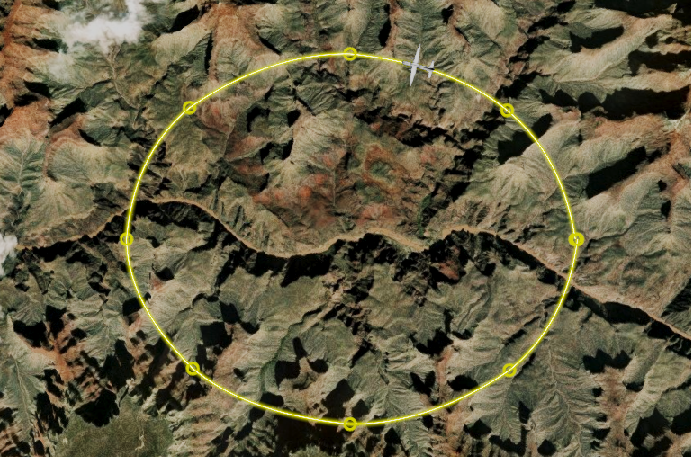
关于样条插值
百度百科给的解释是:
样条插值法是一种以可变样条来作出一条经过一系列点的光滑曲线的数学方法。插值样条是由一些多项式组成的,每一个多项式都是由相邻的两个数据点决定的,这样,任意的两个相邻的多项式以及它们的导数(不包括仇阶导数)在连接点处都是连续的。
一位搞游戏引擎开发的博主在博客上是这样的说的:
在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。插值可以用于填充图像变换时像素之间的空隙。插值,拟合,逼近是数值分析的三大基础工具,通俗意义上它们的区别在于:插值是已知点列并且完全经过点列;拟合是已知点列,从整体上靠近它们,逼近是已知曲线,或者点列,通过逼近使得构造的函数无限靠近它们。科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合。
插值问题的提法是:假定区间[a,b]上的实值函数f(x)在该区间上 n+1个互不相同点x0,x1……xn 处的值是f (x0),……f(xn),要求估算f(x)在[a,b]中某点x的值。基本思路是,找到一个函数P(x),在x0,x1……xn 的节点上与f(x)函数值相同(有时,甚至一阶导数值也相同),用P(x)的值作为函数f(x*)的近似。简单地讲就是已知数据上的若干值,为其补上未知的值。
样条方程是一类分段光滑、并且在各段交接处也有一定光滑性的函数。样条一词来源于工程绘图人员为了将一些指定点连接成一条光顺曲线所使用的工具,即富有弹性的细木条或薄钢条。由这样的样条形成的曲线在连接点处具有连续的坡度与曲率。分段低次多项式、在分段处具有一定光滑性的函数插值就是模拟以上原理发展起来的,它克服了高次多项式插值可能出现的振荡现象,具有较好的数值稳定性和收敛性,由这种插值过程产生的函数就是多项式样条函数。
Cesium中的样条插值
在cesium里,提供了三种样条插值方法,LinearSpline,CatmullRomSpline,HermiteSpline。
在具体的实例上,可以使用样条插值法利用已知的控制点,插值出一系列的点,用于平滑曲线,特别是在路径的追朔重演。
下面,我们分别介绍这三种样条插值的使用方法以及效果。
更多详情见小专栏此文章:GIS之家cesium小专栏
文章提供源码,对本专栏感兴趣的话,可以关注一波
GIS之家源码咨询:GIS之家webgis入门开发系列demo源代码咨询
扫码关注GIS之家微信公众号,回复“gis”可免费获取地图数据以及arcgis系列安装包等资源



