MATLAB SPECTROGRAM
spectrogram
例子
Fs = 1000; t = 0:1/Fs:2-1/Fs; y = chirp(t,100,1,200,'quadratic'); spectrogram(y,100,80,100,Fs,'yaxis') view(-77,72) shading interp colorbar off
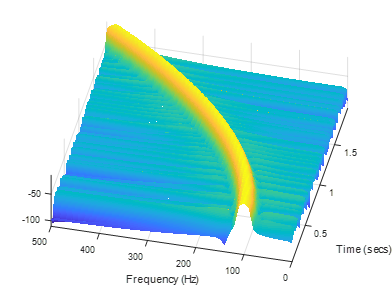
[s,f,t,p] = spectrogram(y,100,80,100,Fs); [q,nd] = max(10*log10(p)); hold on plot3(t,f(nd),q,'r','linewidth',4) hold off colorbar view(2)
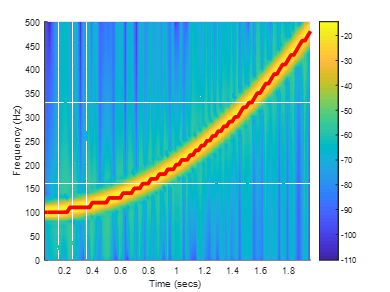
其中，f是51*1的矩阵频率，s是51*96的复矩阵振幅，p是51*96的矩阵，t是1*96的矩阵时间。
某频段的时谱图，设当f为200时，其index为21，则t和s
plot(t,abs(s(21,:)))
或者频谱图应为plot(f, abs(s(21,:)))
功能：使用短时傅里叶变换得到信号的频谱图。
语法：
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
[S,F,T,P]=spectrogram(x,window,noverlap,F,fs)
说明：当使用时无输出参数，会自动绘制频谱图；有输出参数，则会返回输入信号的短时傅里叶变换。当然也可以从函数的返回值S,F,T,P绘制频谱图，具体参见例子。
参数：
x---输入信号的向量。默认情况下，即没有后续输入参数，x将被分成8段分别做变换处理，
如果x不能被平分成8段，则会做截断处理。默认情况下，其他参数的默认值为
window---窗函数，默认为nfft长度的海明窗Hamming
noverlap---每一段的重叠样本数，默认值是在各段之间产生50%的重叠
nfft---做FFT变换的长度，默认为256和大于每段长度的最小2次幂之间的最大值。
另外，此参数除了使用一个常量外，还可以指定一个频率向量F
fs---采样频率，默认值归一化频率
Window---窗函数，如果window为一个整数，x将被分成window段，每段使用Hamming窗函数加窗。如果window是一个向量，x将被分成length(window)段，每一段使用window向量指定的窗函数加窗。所以如果想获取specgram函数的功能，只需指定一个256长度的Hann窗。
Noverlap---各段之间重叠的采样点数。它必须为一个小于window或length(window)的整数。其意思为两个相邻窗不是尾接着头的，而是两个窗有交集，有重叠的部分。
Nfft---计算离散傅里叶变换的点数。它需要为标量。
Fs---采样频率Hz，如果指定为[]，默认为1Hz。
S---输入信号x的短时傅里叶变换。它的每一列包含一个短期局部时间的频率成分估计，
时间沿列增加，频率沿行增加。
如果x是长度为Nx的复信号，则S为nfft行k列的复矩阵，其中k取决于window，
如果window为一个标量，则k = fix((Nx-noverlap)/(window-noverlap))
如果window为向量，则k = fix((Nx-noverlap)/(length(window)-noverlap))
对于实信号x，如果nfft为偶数，则S的行数为(nfft/2+1)，如果nfft为奇数，
则行数为(nfft+1)/2，列数同上。
F---在输入变量中使用F频率向量，函数会使用Goertzel方法计算在F指定的频率处计算频谱图。指定的频率被四舍五入到与信号分辨率相关的最近的DFT容器(bin)中。而在其他的使用nfft语法中，短时傅里叶变换方法将被使用。对于返回值中的F向量，为四舍五入的频率，其长度等于S的行数。
T---频谱图计算的时刻点，其长度等于上面定义的k，值为所分各段的中点。
P---能量谱密度PSD(Power Spectral Density)，对于实信号，P是各段PSD的单边周期估计；
对于复信号，当指定F频率向量时，P为双边PSD。
P矩阵的元素计算公式如下P(I,j)=k|S(I,j)|2，其中的的k是实值标量，定义如下
对于单边PSD，计算公式如下，其中w(n)表示窗函数，Fs为采样频率，在0频率和奈奎斯特频率处，分子上的因子2改为1；
参考
http://blog.sina.com.cn/s/blog_6163bdeb0102dwfw.html
