拉格朗日乘子法与对偶问题分析
引言
拉格朗日乘子法和原始问题与对偶问题的转换,最近总被人提到,我对网上的教程和书上的知识进行学习,尝试从公式上进行理解,对于几何中的理解稍微会接触到,简单做下笔记以防自己遗漏(防peach🐕)
拉格朗日乘子法
简介
拉格朗日乘子法是用来求解带约束条件的最优化的问题的方法,分为带等式约束和不等式约束。
但是拉格朗日求出来的是局部最值,只有在凸优化的情况下才能确保是全局最值,所以我们将拉格朗日求出来的解称为可行解
等式约束
\(\min_ \limits{x} f(x) \qquad (1) \\ s.t. h_i(x)=0,i=1,2...m \qquad (2)\)
-
几何解释
为了方便直观的解释,将m视作1。在图中画出f(x)的等值线和h(x,y)=0的约束条件。
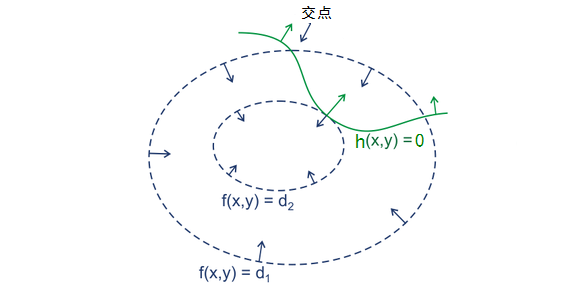

观察到当f(x)取到最小值时,h(x,y)与相应的等值线相切,对应点的梯度向量共线。即\(\nabla_x f(x)=\alpha\nabla_x h(x)\) -
数学警告⚠
\(L(x,\alpha)=f(x)+\sum_{i=1}^m\alpha_i h_i(x) \qquad (3) \\ \nabla_xL(x,\alpha)=0 \qquad (4) \\ \nabla_\alpha L(x,\alpha)=0 \\ \Longleftrightarrow each\quad h_i(x)=0 \qquad(5)\)
(3)式为构造的拉格朗日函数,因为\(h_i(x)=0\)成立,所以\(L(x,\alpha)\)的极值点也是f(x)的极值点,故可以转换为对\(L(x,\alpha)\)的无约束条件求极值点。
(4)式是\(L(x,\alpha)\)能取到极值点的必要条件,这里也印证了集合解释中的相切。
(5)式表明\(L(x,\alpha)\)中除了变量\(\alpha\)外其他的变量x都限定在了指定函数\(h_i(x)=0\)下
通过(4)(5)式可得\(L(x,\alpha)\)的极值点也就是f(x)的极值点。
不等式约束
\(\min_ \limits{x} f(x) \qquad (6) \\
s.t. g_i(x)<=0,i=1,2...m \qquad (7)\)
以m=1为例
\(L(x,\lambda)=f(x)+\lambda g(x) \qquad (8)\)
-
几何解释
f(x)要么在g(x)<0的区域上找到极值点点,要么在g(x)=0的边界上找到极值点

g(x)<0,如上左图中在g(x)<0的区域上找极值点,那么只要直接对f(x)进行求导就可以了,即\(\lambda=0\)
g(x)=0,如上右图中在g(x)=0的边界上找极值点,等价于约束优化问题。即\(g(x)=0\)
无论在什么情况下,\(\lambda g(x)=0\)恒成立,保证了优化问题的目标没有改变 -
数学警告⚠
对于\(\lambda(\neq 0)\)的取值
最小化问题:边界上,f(x)的法向量指向区域内,因为在整个区域上在边界上取到最小值,内部的一定比取到的大。而g(x)边界上的法向量指向区域外,因为约束条件是g(x)<0。故λ>0。
最大化问题:边界上,f(x)的法向量指向区域外,因为在整个区域上在边界上取到最大值,内部的一定比取到的小。而g(x)边界上的法向量指向区域外,因为约束条件是g(x)<0。故λ<0。 -
求解
根据上面的解释发现,不等式约束优化问题需要一定的约束,构造的拉格朗日函数的优化目标与原始目标相同。
\(\min_ \limits{x} f(x) \qquad (9) \\
s.t. h_i(x)=0,i=1,2...m \qquad (10) \\
\quad g_j(x)<=0,j=1,2...n \qquad (11) \\
L(x,\alpha,\lambda)=f(x)+\sum^m_ \limits{i=1}\alpha_ih_i(x)+\sum^n_ \limits{j=1}\lambda_jg_j(x) \qquad (12)\)
可利用的方程:
\(\nabla_xL(x,\alpha,\lambda)=0 \\
h_i(x)=0,i=1,...,m \\
g_j(x)<=0,j=1,...,n \\
\lambda_j>=0,j=1,...,n\)
利用拉格朗日乘子法求解不等式约束问题不一定成功的,除非对偶问题与这个原始问题之间是强对偶性,才能利用KKT条件,这里可利用的方程只是KKT条件的一部分。
对偶问题分析
简介
每个线性规划问题都有一个与之对应的对偶问题(极大极小值问题的转换),对偶问题有良好的特性。
1.无论原始问题是否是凸的,对偶问题都是凸优化问题。
2.对偶问题可以给出原始问题一个下界。
3.当满足一定条件(slater条件,KKT条件)时,原始问题与对偶问题是完全等价的(强对偶性)。
对偶问题
-
原始问题
\(\min_\limits{x} f(x) \\ s.t. h_i(x)=0,i=1,2,...,m \\ \qquad g_j(x)<=0,j=1,2,...,n \\ Lagrangian:\\ L(x,\alpha,\lambda)=f(x)+\sum^m_{i=1}\alpha_ih_i(x)+\sum^n_{j=1}\lambda_jg_j(x)\)
因为约束条件的存在,所以\(f(x)=\max_\limits{\alpha\lambda;\lambda_j>=0}L(x,\alpha,\lambda)\)
故\(\min_\limits{x} f(x)=\min_\limits{x}\max_\limits{\alpha\lambda;\lambda_j>=0}L(x,\alpha,\lambda)\),将原始的最优化问题转化成了广义拉格朗日函数的极小极大问题。
定义原始问题的最优值\(p^*=\min_ \limits{x} f(x)\)
对原始问题进行利用拉格朗日乘子法相当于不等式约束求解,无法求出。 -
对偶问题
1.引入对偶函数\(D(\alpha,\lambda)\)
\(D(\alpha,\lambda)=\min_\limits{x}L(x,\alpha,\lambda)\)
2.对偶问题形式
\(\max_\limits{\alpha\lambda;\lambda_j>=0}D(\alpha,\lambda)=\max_\limits{\alpha\lambda;\lambda_j>=0}\min_\limits{x}L(x,\alpha,\lambda)\)
3.最优解\(d^*\)
\(d^*=\max_\limits{\alpha\lambda;\lambda_j>=0}D(\alpha,\lambda)\) -
对偶问题与原始问题之间的关系
1.若原始问题和对偶问题都有最优值,则\(d^*<=p^*\),通过对偶性为原始问题引入一个下界。
证明:
\(D(\alpha,\lambda)=\min_ \limits{x}L(x,\alpha,\lambda)\leq L(x,\alpha,\lambda)\leq\max_\limits{\alpha\lambda;\lambda_j>=0}L(x,\alpha,\lambda)=f(x)\)
\(d^*=\max_\limits{\alpha\lambda;\lambda_j>=0}D(\alpha,\lambda)\leq\min_\limits{x}f(x)=p^*\)
2.\(d^*\leq p^*\)是弱对偶性,\(d^*=p^*\)是强对偶性。在强对偶型的条件下,可以通过求解对偶问题来求解原始问题获得最优解。
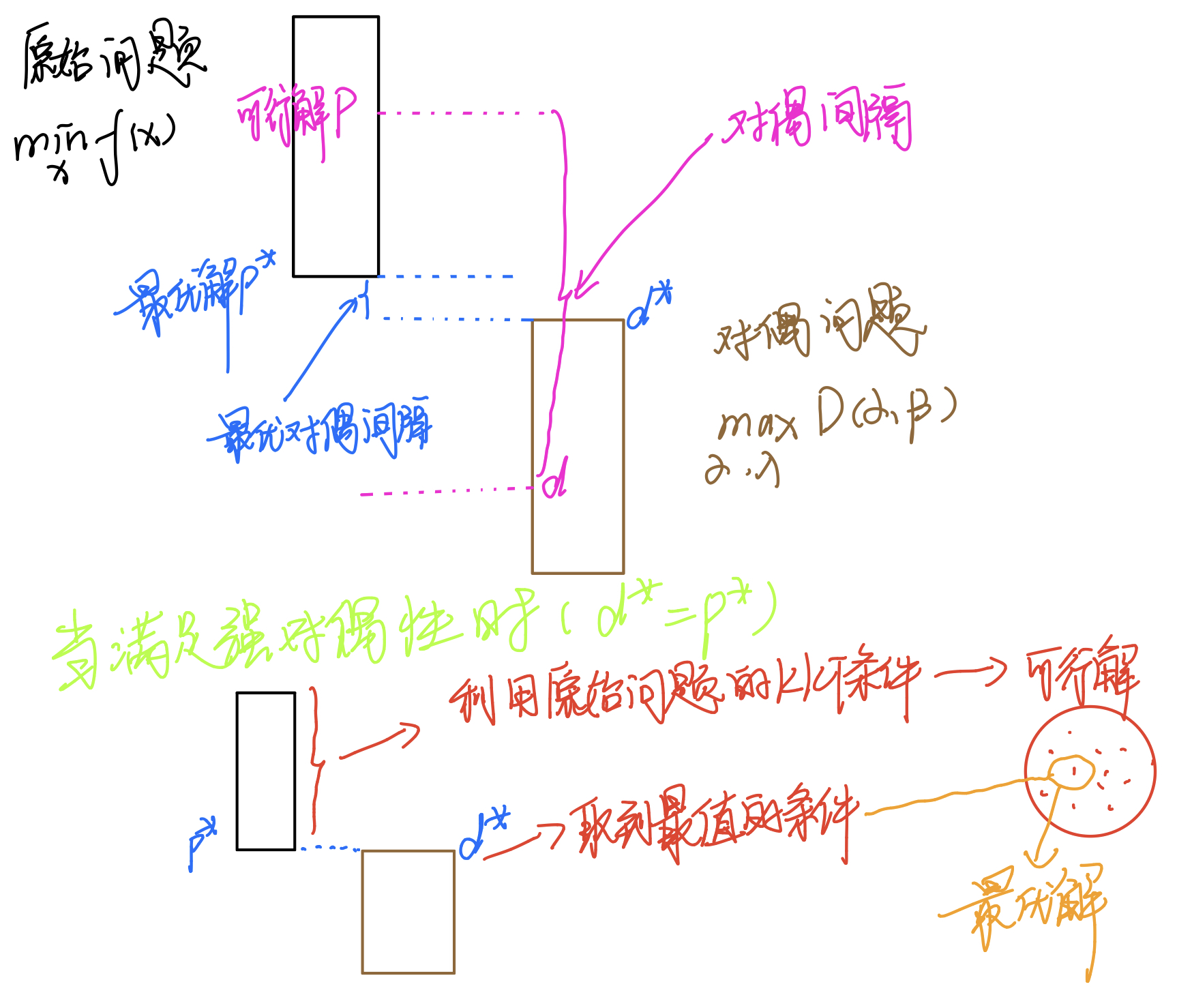
3.slater条件:\(f(x),g_j(x)\)是凸函数,\(h_i(x)\)是仿射函数(最高次项为1的多项式函数),并且\(g_j(x)\)是严格可行的(存在x,对所有j有\(g_j(x)<0\)),则存在\(x^*,\alpha^*,\lambda^*\),使得\(x^*\)是原始问题的解,\(\alpha^*,\lambda^*\)是对偶问题的解,同时\(d^*=p^*=L(x^*,\alpha^*,\lambda^*)\)。也就是原始问题和对偶问题之间是强对偶性,满足上图下面那个图形的条件,原始问题的最小值等于对偶问题的最大值。而又因为对偶问题是凸优化问题,所以求出对偶问题的解来解决原始问题。
求解对偶问题的过程,分为极小化拉格朗日函数和极大化对偶函数:
第一步:极小化拉格朗日函数,可以列出下面的可利用的方程:
\(\nabla_xL(x^*,\alpha^*,\lambda^*)=0 \qquad KKT1\\
h_i(x^*)=0,i=1,...,m \qquad KKT2\\
g_j(x^*)<=0,j=1,...,n \qquad KKT3\\
\lambda_j^*>=0,j=1,...,n \qquad KKT4\)
细心的人就已经发现了这就是解决不等式约束问题的可利用方程,同时也是对原始问题求解的过程,相当于求出一堆可行解,但是还缺少了方程。
PS:参数加上*是因为此时已经将可以确定参数了。
第二步:极大化对偶函数,可以利用的方程:
\(\lambda_j^*g_j(x^*)=0,j=1,...,n \qquad KKT5\)
KKT5称为对偶互补松弛条件,相当于上图右下方在可行解中取出最优解。
这5个条件合在一起称为KKT条件。通过KKT条件可以解出不等式约束的最优化问题。
有时间再去更新添加一个例子
参考书籍和博客内容:
人生此处,绝对乐观

