被遗忘 Java位运算符

　　撸了这么多年的Java代码，突然发现对于位运算符尽然知之甚少，在阅读源码过程中对于"&&"与"&"，">>"与">>>"的差异还不胜了解，今天就将自己理解做个记录以便大家指正。

　　简介：关于位运算符无非也就 与(&)、或(|)、异或(^)、取反(~)、左移(<<)、右移(>>)、无符号右移(>>>)，位运算其实就是二进制的运算，加减乘除适用于十进制，而位运算就是二进制的运算,但是由于我们的运算都是基于十进制来说的。

 　　引申：什么是二进制？

 　　　　我们在编码过程中应该会了解很多不同的进制，除去常用的十进制，还有二进制、八进制、十六进制，因为我们的位运算符主要用到二进制，就只讲讲二进制，几进制就是一个位上最多能表示几个数，如十进制的个位有0~9十个数字，八进制有0~7八个数字，二进制我们自然想到就是0~1两个数字。

 

　　我们编码中最小的单位应该是字节，而一个字节有8位，每一位就是一个0或1，所以一个字节用二进制表示就是

 

 　　基础：

　　1、与运算符(&)  

 　　使用规则：全一则一，否则为零

 　　如果  4&7   那么这个应该怎么运算呢？

 　　首先我们需要把两个十进制的数转换成二进制 

　　4 ： 0000 0100

       7 ： 0000 0111

　　

　　2、或运算符(|)

　　使用规则：全0为0，否则为1；

　　以 5|9   为例

 　   5 ： 0000 0101 

　　9 ： 0000 1001

　　3、 异或运算符(^)

　　使用规则：相同位0，否则为1；

       以 7^15 为例

       7：   0000 0111

      15： 0000 1111

 

　　4、取反运算符(~)

　　使用规则：遇0则1，遇1则0；

        例：   ~15

        同样的先变成二进制：15：0000 1111

　　5、左移运算(<<)

      左移就是把所有位向左移动几位

     如：   12 << 2    意思就是12向左移动两位

          12的二进制是： 0000 1100

 

　　通过这个图我们可以看出来，所有的位全都向左移动两位，然后把右边空的两个位用0补上，最左边多出的两个位去掉，最后得到的结果就是00110000  结果就是48

　　我们用同样的办法算 12<<3  结果是 96   8<<4  结果是  128

　　由此我们得出一个快速的算法    M << n   其实可以这么算   M << n  = M * 2ⁿ

 

^6、 右移运算符(>>)

 　　这个跟左移运算大体是一样的

        例： 12 >> 2

 

　　我们可以看出来右移和左移其实是一样的，但是还是有点不同的，不同点在于对于正数和负数补位的时候补的不一样，负数补1，正数补0

　　如我们再做一个 –8 的    -8>>2

 

 

　　这里总结一下，关于负数或者正数来说，移位的时候是一样的，但是在补位的时候，如果最高位是0就补0，如果最高位是1就补1

由此我们得出一个快速的算法    M >> n   其实可以这么算   M >> n  = M / 2^n

 

　　7、无符号右移(>>>)

 　　无符号右移(>>>)只对32位和64位有意义

　　在移动位的时候与右移运算符的移动方式一样的，区别只在于补位的时候不管是0还是1，都补0

　　

　　总结：二进制运算符，包括位运算符和移位运算符，使程序员可以在二进制基础上操作数字，可以更有效的进行运算，
 并且可以以二进制的形式存储和转换数据，是实现网络协议解析以及加密等算法的基础。

     

　　题外话：

　　1、二进制转十进制：

　　小数点前或者整数要从右到左用二进制的每个数去乘以2的相应次方并递增,小数点后则是从左往右乘以二的相应负次方并递减。

　　

　　

　　2、十进制转二进制

　　2.1、正整数的十进制转换二进制：
　　　　要点：除二取余，倒序排列
　　　　解释：将一个十进制数除以二，得到的商再除以二，依此类推直到商等于一或零时为止，倒取将除得的余数，即换算为二进制数的结果
　　　　例如把52换算成二进制数，计算结果如图：
　　　　  

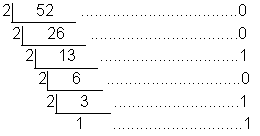
　　　　52除以2得到的余数依次为：0、0、1、0、1、1，倒序排列，所以52对应的二进制数就是110100。
　　　　由于计算机内部表示数的字节单位都是定长的，以2的幂次展开，或者8位，或者16位，或者32位....。
　　　　于是，一个二进制数用计算机表示时，位数不足2的幂次时，高位上要补足若干个0。本文都以8位为例。那么：
　　　　(52)10=(00110100）

　　

　　2.2、负整数转换为二进制

　　　　要点：（正数除二取余，倒序排列）取反加一
　　　　解释：将该负整数对应的正整数先转换成二进制，然后对其“取补”，再对取补后的结果加1即可
　　　　例如要把-52换算成二进制：
　　　　1.先取得52的二进制：00110100
　　　　2.对所得到的二进制数取反：11001011
　　　　3.将取反后的数值加一即可：11001100
　　　　即：(-52)10=(11001100)2
　　　　


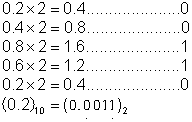
　　2.3、小数转换为二进制
　　　　要点：（小数）乘二取整，正序排列
　　　　解释：对被转换的小数乘以2，取其整数部分(0或1)作为二进制小数部分，取其小数部分，再乘以2，又取其整数部分作为二进制小数部分，然后取小数部分，再乘以2，直到小数部分为0或者已经去到了足够位数。每次取的整数部分，按先后次序排列，就构成了二进制小数的序列
　　　　例如把0.2转换为二进制，转换过程如图：
　　　　 
　　　　0.2乘以2，取整后小数部分再乘以2，运算4次后得到的整数部分依次为0、0、1、1，结果又变成了0.2，
　　　　若果0.2再乘以2后会循环刚开始的4次运算，所以0.2转换二进制后将是0011的循环，即：
　　　　(0.2)10=(0.0011 0011 0011 .....)2
　　　　循环的书写方法为在循环序列的第一位和最后一位分别加一个点标注