有限厚度 vs 周期性结构

写在前面

本文将以二维 Weyl的哈密顿量为例

哈密顿量

\[H(k_x,k_y)=v(k_x\sigma_x+k_y\sigma_y) + \frac{\Delta}{2}\sigma_z + E_f\sigma_0 \]

这里, \(v\) 是费米速度, \(\Delta\) 是带隙, Weyl 锥关于 \(E=E_f\) 上下对称.

离散化哈密顿量

我们将该哈密顿量离散到下图的网格上.

离散 \(x,y\) 方向

对 \(x,y\) 两个方向离散化, 假设沿着 \(x,y\) 的宽度分别为 \(W, L\).
矩阵元为:

\[H_{00}=\begin{pmatrix} \frac{\Delta}{2}\sigma_z + E_f\sigma_0 & \frac{1j}{2a_x}v\sigma_x & & \\ -\frac{1j}{2a_x}v\sigma_x & \frac{\Delta}{2}\sigma_z + E_f\sigma_0 & \frac{1j}{2a_x}v\sigma_x & \\ & \cdots & \cdots & \cdots \\ & & \cdots & \cdots \\ \end{pmatrix} _{W\times W}\\ H_{01}=\begin{pmatrix} \frac{1j}{2a_y}v\sigma_y & & & & \\ & \frac{1j}{2a_y}v\sigma_y & & & \\ && \cdots & & \\ & & & & \cdots \\ \end{pmatrix} _{W\times W} \]

其中 \(a_x,a_y\) 是沿着 \(x,y\) 方向离散化的最小网格 grid spacing.

计算能带

\[H(k_y) = H_{00} + e^{ik_ya_y}H_{01}+ e^{-ik_ya_y}H_{10} \]

结果为:

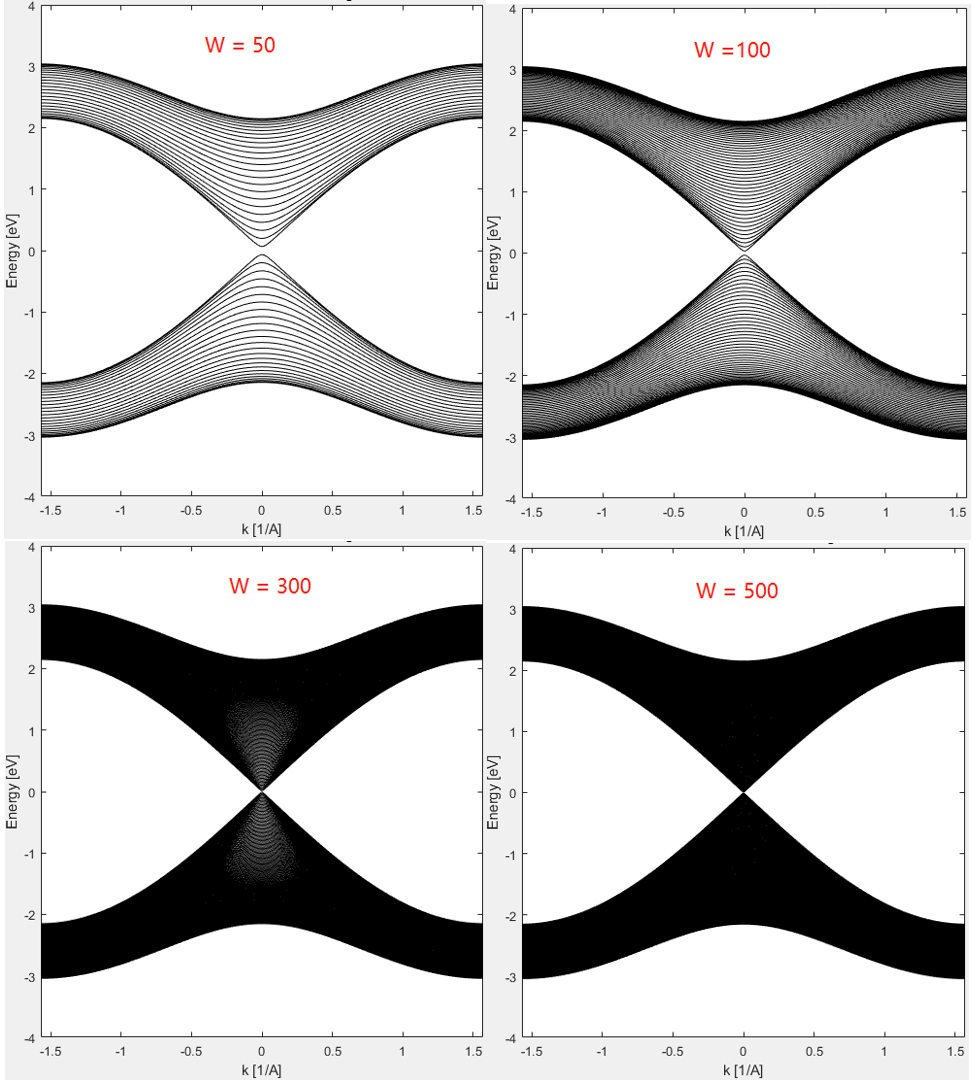
只离散 \(y\) 方向, \(x\)方向仍周期性

不难得到

\[H_{00}(k_x) = vk_x\sigma_x + \frac{\Delta}{2}\sigma_z + E_f\sigma_0\\ H_{01}(k_x) = \frac{1j}{2a}v\sigma_y \\ \]

其中 \(a\) 是沿着 \(y\) 方向离散化的最小网格.

计算能带

\[H(k_y) = \sum_{k_x}\left(H_{00}(k_x) + e^{ik_ya_y}H_{01}+ e^{-ik_ya_y}H_{10}\right) \]

结果为:

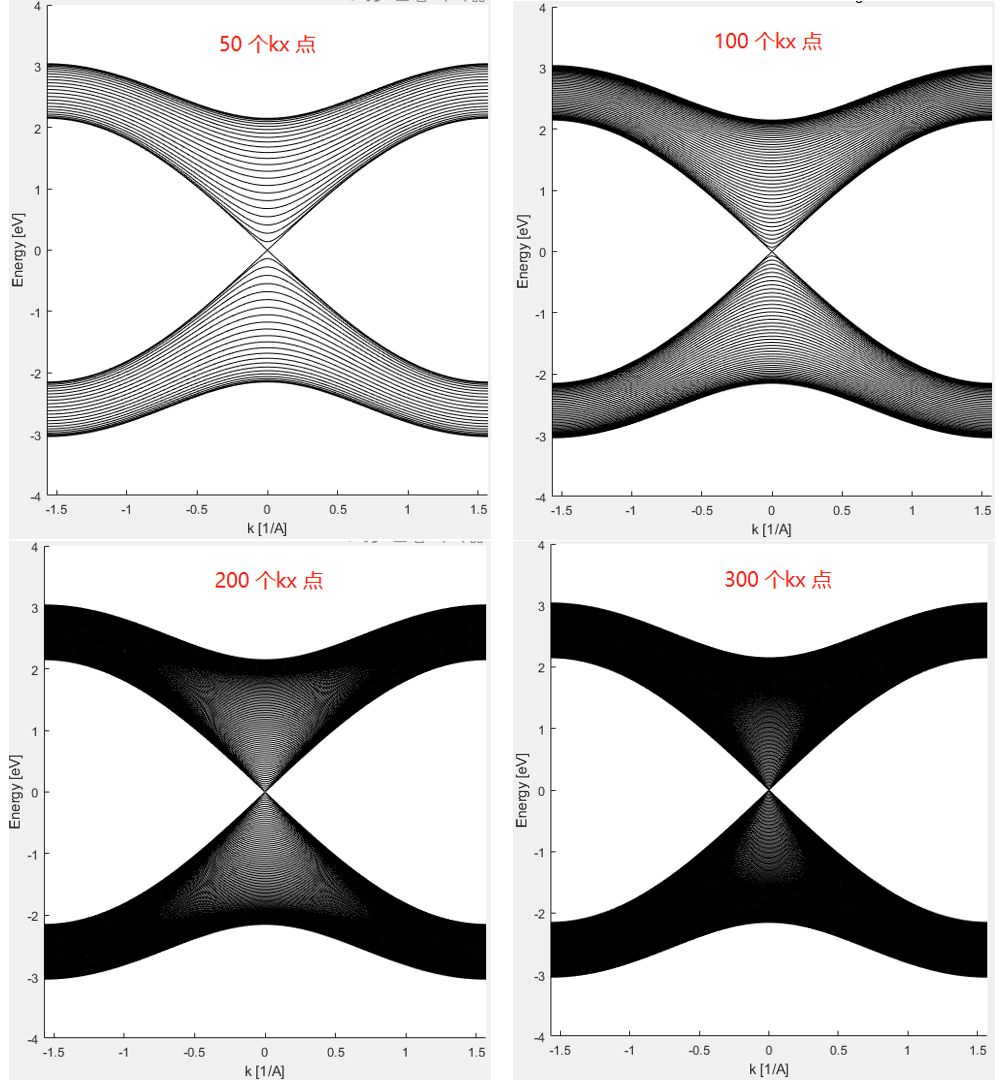
对比

不难发现, 当厚度足够大时，此时可以用周期性结构描述. 但是当有限厚度时，例如 \(W = 50\), 该体系存在带隙.

附件(matlab代码)

点击查看代码 weyl_ham_plot.m

clear all;
W = 10;
v = 2.15;
%v = 1.3;

m = 0;
%m = 1;
Ef = 0;
%Ef = 2.5;
[H00,H01] = weyl_ham(v,m,Ef,W);

Nk = 500;
k = linspace(-pi/2,pi/2,Nk);
res = zeros(Nk,2*W);
for i = 1:Nk
    Ham = H00 + H01*exp(1j*k(i)) + H01'*exp(-1j*k(i));
    val = eig(Ham);
    res(i,:) = sort(real(val));
end
figure;
plot(k,res,'k');
xlim([-pi/2,pi/2]);
title('The bandstructure of Center region')
xlabel('k [1/A]');
ylabel('Energy [eV]')

点击查看代码 weyl_ham.m

function [H00,H01] = weyl_ham(v,m,Ef,W)
    % H = v*(sigma_x*kx + sigma_y*ky) + m/2*sigma_z + Ef*sigma_0;
    % Pauli Matrices
    sigma_x = [[0,1];[1,0]];sigma_y = [[0,-1j];[1j,0]];
    sigma_z = [[1,0];[0,-1]];sigma_0 = [[1,0];[0,1]];
    a = 1;%A
    H00 = zeros(2*W,2*W);
    H01 = zeros(2*W,2*W);
    for j = 1:W
        H00(2*j-1:2*j,2*j-1:2*j) = m/2*sigma_z + Ef*sigma_0 ;
        H01(2*j-1:2*j,2*j-1:2*j) = v/(2j*a)*sigma_y;
        if j < W
            H00(2*j-1:2*j,2*j+1:2*j+2) = v/(2j*a)*sigma_x;
            H00(2*j+1:2*j+2,2*j-1:2*j) = -v/(2j*a)*sigma_x;
        end
    end
end

点击查看代码 weyl_ham_k_plot.m

%%%%%%%%%%%%%%%%%%%%%%%%%%% Band of each slice %%%%%%%%%%%%%%%%%%%%%%%%%%%%
Nk = 500;
k = linspace(-pi/2,pi/2,Nk);
res = zeros(Nk,2);
figure;

v = 2.15; delta = 0;Ef = 0; m = 0.0;
tmp = 1; N_kx = 50;
kx = linspace(0,tmp*pi,N_kx);
for j = 1: N_kx
    for i = 1:Nk
        [H00,H01] = weyl_ham_k(v,delta,Ef,m,kx(j));
        Ham = H00 + H01*exp(1j*k(i)) + H01'*exp(-1j*k(i));
        val = eig(Ham);
        res(i,:) = sort(real(val));
    end

hold on;
plot(k,res,'k');
%ylim([-3,3]);
xlim([-pi/2,pi/2]);
title('The bandstructure of Center region')
xlabel('k [1/A]');
ylabel('Energy [eV]')
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

点击查看代码 weyl_ham_k.m

function [H00,H01] = weyl_ham_k(v,delta,Ef,m,kx)
    % H = v*(sigma_x*kx + sigma_y*ky) + delta/2*sigma_z + Ef*sigma_0 + m*(sinkx^2+sinky^2);
    % Pauli Matrices
    sigma_x = [[0,1];[1,0]];sigma_y = [[0,-1j];[1j,0]];
    sigma_z = [[1,0];[0,-1]];sigma_0 = [[1,0];[0,1]];
    a = 1;%A
    H00 = delta/2*sigma_z + Ef*sigma_0 + v*sin(kx)*sigma_x + (m*(sin(kx))^2 + 2*m/a^2)*sigma_0;
    H01 = 1j/(2*a)*v*sigma_y - m/a^2;
    %H10 = -1j/(2*a)*v*sigma_y - m/a^2;
end