The k·p Hamiltonian of graphene
graphene
先看最经典的 石墨烯 RMP 论文

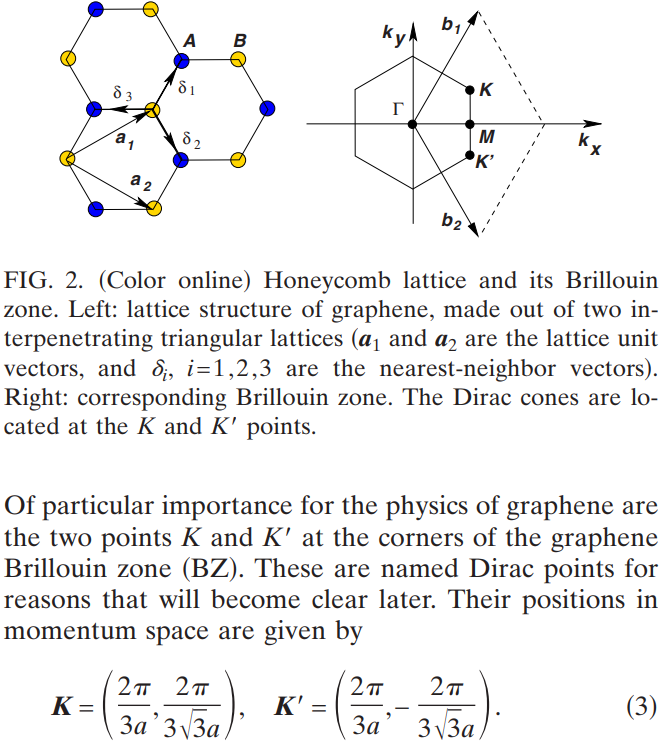
石墨烯的空间群是 ,点群是 ,在 点处的波矢群是 .
点波矢群推导
石墨烯的空间群是 ,点群是 ,生成元有 . 下面来推导 点处的波矢群(以六方格子中心为坐标原点)。
点分数坐标为 , 点在生成元下的操作:
: 到 , 到 ,那么:
: 到 , 到 ,那么:
因此, 点处没有空间反演对称性,时间反演对称操作同理。
操作,类似与镜面对称,即垂直于 [100] 方面的镜面。其操作为: 到 , 到 ,那么得到:
所以 的波矢群是 , 生成元为 。
点处 哈密顿量推导
已知 Dirac 锥的费米面附近的轨道为 A 和 B 子格的 轨道。以 为基矢。
点附近存在 ,生成元有 。
因为波函数存在相位 ,在 对称操作下,
A 子格移动到 A', , ;
B 子格移动到 B', , 。
的表示矩阵为:
在镜面对称作用下,A 子格到 B 子格,B 子格到 A 子格, 但是会存在相位。
A 子格移动到 B, ;
B 子格移动到 A, .
的表示矩阵为:
PRL 108, 196802 (2012)
参考PRB 103,035308(2021):
得到:
参考:
Phys. Rev. Lett. 99, 236809(2007)
Phys. Rev. Lett. 108, 196802(2012)
Phys. Rev. B 102, 235435(2020)
Phys. Rev. B 103, 035308(2021)
附录
点 哈密顿量 Qsymm 程序:
点击查看代码
import sympy,sys
import qsymm
import numpy as np
C = qsymm.chiral(2, U=np.array([[1, 0], [0, -1]]))
C3 = qsymm.groups.rotation(1/3, U=np.diag(np.exp(2j * np.pi / 3 * np.array([1, -1]))))
M = qsymm.mirror([1,0],U=np.array([[0, np.exp(2j*np.pi/3)], [np.exp(-2j*np.pi/3), 0]]))
dim = 2
total_power = 1
#symmetries = [C3]
#family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
#qsymm.display_family(family)
'''
Matrix([[1, 0], [0, 0]])
Matrix([[0, 0], [0, 1]])
Matrix([[0, I*k_x + k_y], [-I*k_x + k_y, 0]])
Matrix([[0, -k_x + I*k_y], [-k_x - I*k_y, 0]])
'''
#symmetries = [M, C3]
#family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
#qsymm.display_family(family)
'''
Matrix([[1, 0], [0, 1]])
Matrix([[0, k_x*(sqrt(3) + I) + k_y*(1 - sqrt(3)*I)], [k_x*(sqrt(3) - I) + k_y*(1 + sqrt(3)*I), 0]])
'''
symmetries = [C, M, C3]
family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
qsymm.display_family(family)
'''
Matrix([[0, k_x*(1 + sqrt(3)*I/3) + k_y*(sqrt(3)/3 - I)], [k_x*(1 - sqrt(3)*I/3) + k_y*(sqrt(3)/3 + I), 0]])
'''





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现