常见的半导体 k·p 哈密顿量

背景

众所周知，如今工业界大规模采用的半导体材料主要以 Si, Ge, III-V 族材料为主。它们的晶格结构大多数是金刚石结构 (Diamond)，闪锌矿结构 (Zinblende)，纤锌矿结构 (Wurtzite)等，详见半导体材料的基本知识 - ghzphy - 博客园 (cnblogs.com)。在凝聚态物理或者材料科学中，体系的哈密顿量一直是研究的重点，掌握使用材料的哈密顿量对理解和计算材料的各种性质十分关键，而且在现有成熟的 TCAD 等 EDA 工具中，在材料的物理性质部分，给出该体系的 k·p 哈密顿量参数信息。原则上讲，有了体系的哈密顿量，即可得到该材料的的所有物理信息，例如带边有效质量，迁移率等等。自上个世纪五六十年代以来，E. O. Kane 和 J. M. Luttinger 等人基于群论知识，发展了一套成熟的 k·p 方法，即在一些高对称操作限制下，这些晶格存在着固定的特殊的 k·p 哈密顿量形式。对于不同空间群晶格，研究者们分别给出了不同的多带 k·p 模型，但是，这些方法操作十分复杂，且需要结合手动推导，容易出现错误。近年来，一些自动化求解体系的 k·p 哈密顿量的程序包也不断地涌现出来，例如，kdot_symmetry, Qsymm, MagnetKP 等等，它们的出现极大地方便了研究者去探索各种材料的物理性质。本文主要结合 Qsymm 程序来计算常见的半导体 k·p 哈密顿量。(主要参考 The k p Method | SpringerLink )

Dresslhaus-Kip-Kittel (DKK) Model

我们首先来研究不考虑自旋下的金刚石结构的 k·p 哈密顿量。下图是简单的能带示意图，在不考虑自旋情况下，在 Γ 点处，能带是三重简并的，查询特征标表可知是属于 Γ₂₅⁺表示。

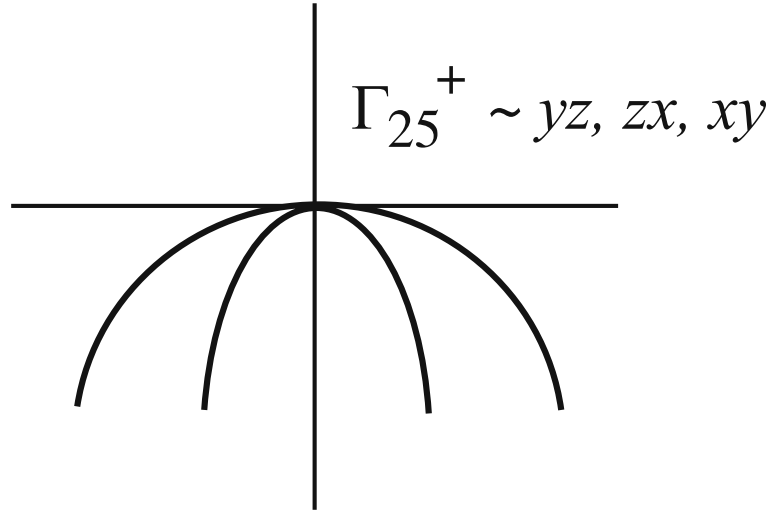
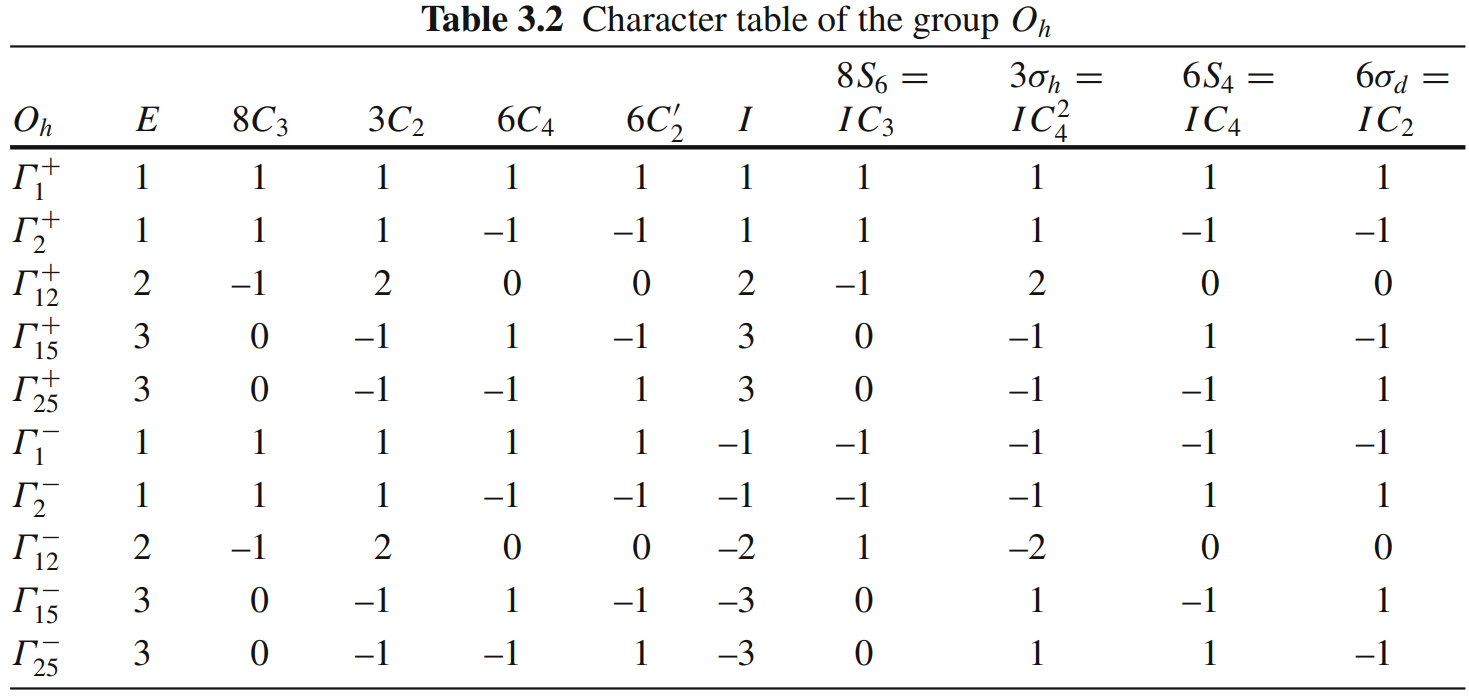
三个波函数有着: ε₁⁺ → yz, ε₂⁺ → zx, ε₃⁺ → xy，这里的 + 表示宇称。

对于一阶微扰矩阵元：

因为 ε_r⁺ 是偶函数，而 k·p 是奇函数，积分可知该矩阵元为 0。用群论的语言表述，ε_r⁺属于 Γ₂₅⁺表示，k·p 是属于 Γ₁₅⁺表示，Γ₂₅⁺ ×Γ₁₅^- × Γ₂₅⁺不包含 Γ₁⁺，因为该矩阵元结果是个标量，应该不随任何对称操作而变化，而 Γ₁⁺是唯一的标量表示，如果直积的结果不含有 Γ₁⁺，则表示该矩阵元不存在。因此，得接着考虑二阶微扰，最后可得哈密顿量为:

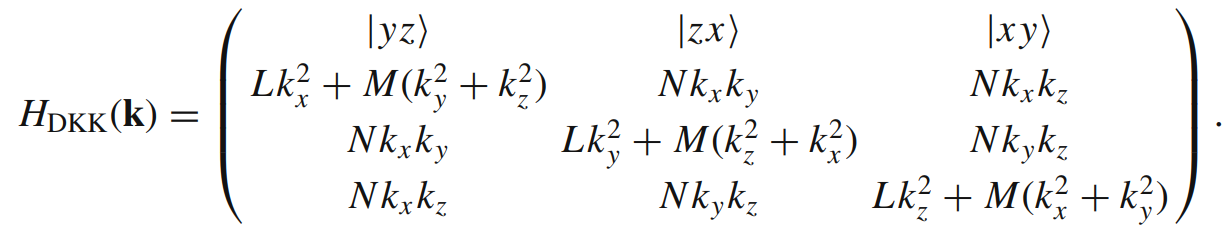
可知该 DKK 哈密顿量有三个参数，分别是 L, M, N 等。

下面，我们来利用 Qsymm 程序自动化产生该金刚石的 DKK 哈密顿量。

自动化产生哈密顿量方法流程如下，

1. 首先要确定波函数，即哈密顿量的基矢波函数形式

2. 确定材料的空间群点群，找到点群生成元的三维实空间的表示。

3. 找到生成元在基矢波函数下的矩阵表示

对于本节中的金刚石结构，属于 Oh 点群，点群生成元可通过数据库查询，例如 3D Point Groups GENPOS (ehu.es) 得到 Oh点群的生成元为 C_2z, C_2y, C_3,111, C_2,110, P

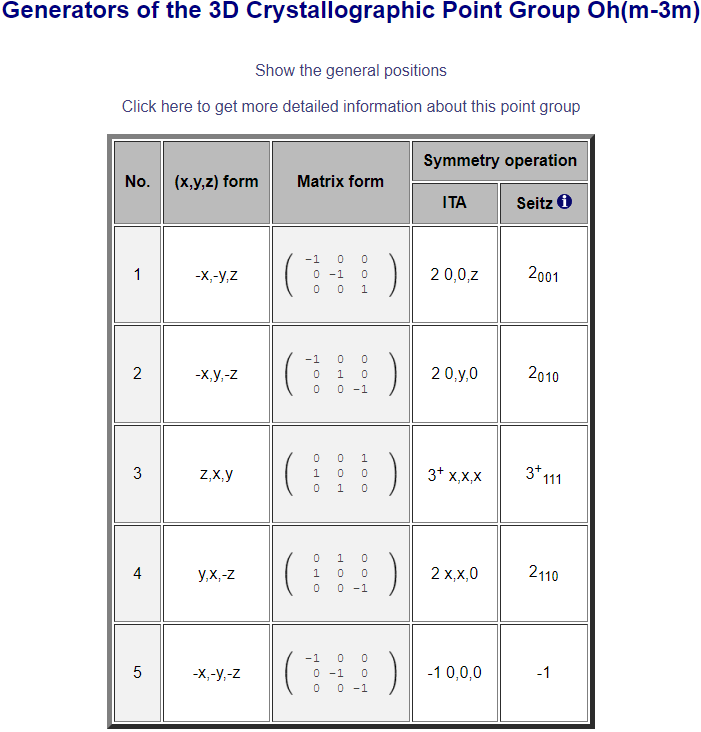
该生成元实空间表示矩阵如图所示，再以 ε₁⁺ → yz, ε₂⁺ → zx, ε₃⁺ → xy 为基矢，得到生成元在该波函数下的表示矩阵。

# Spatial inversion
pU = np.array([
    [1.0, 0.0, 0.0],
    [0.0, 1.0, 0.0],
    [0.0, 0.0, 1.0]
])

# Rotation: C3z
rotU = np.array([
    [0.0, 0.0, 1.0],
    [1.0, 0.0, 0.0],
    [0.0, 1.0, 0.0],
])

# Rotation: C2y
rotU = np.array([
    [-1.0, 0.0, 0.0],
    [0.0, 1.0, 0.0],
    [0.0, 0.0, -1.0],
])

# Rotation: C2_110
rotU = np.array([
    [0.0, -1.0, 0.0],
    [-1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0],
])

View Code

运行 Qsymm 代码 (见附录)，即可自动化生成 DKK 哈密顿量，得到:

Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
Matrix([[k_y**2 + k_z**2, 0, 0], [0, k_x**2 + k_z**2, 0], [0, 0, k_x**2 + k_y**2]])
Matrix([[k_x**2, 0, 0], [0, k_y**2, 0], [0, 0, k_z**2]])
Matrix([[0, k_x*k_y, k_x*k_z], [k_x*k_y, 0, k_y*k_z], [k_x*k_z, k_y*k_z, 0]])

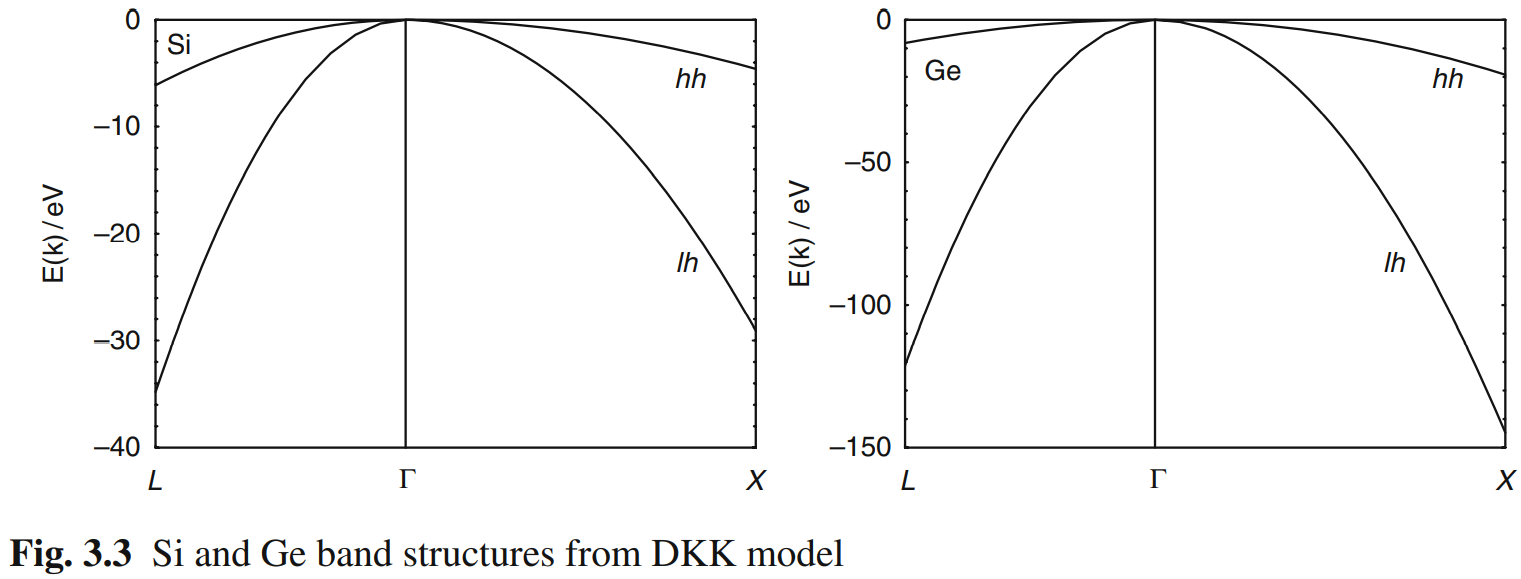
用上述参数拟合得到能带(代码见附录)。

Kane Model

当半导体带隙很小时，需要考虑导带和价带，这里介绍闪锌矿结构的四带 Kane 模型：

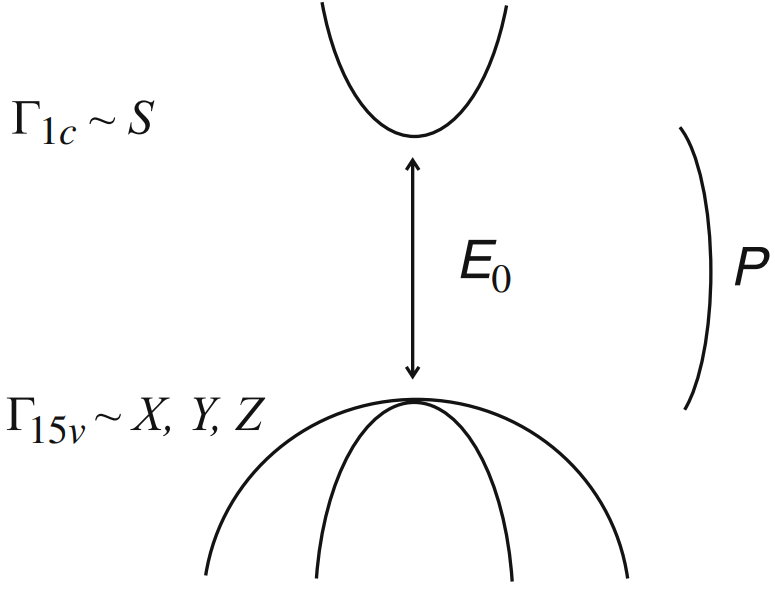
这里的基矢波函数选为 S, X, Y, Z 形式，它们分别属于 Γ₁ 和 Γ₁₅ 表示。

闪锌矿结构点群属于 Td，该点群的生成元为 C_2z, C_2,010, C_3,111, m_1,-1,0。

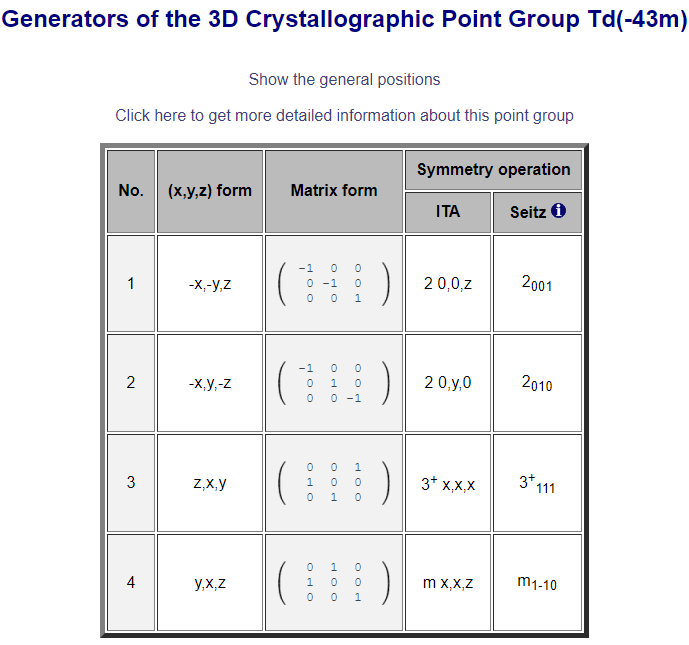
写出各生成元在基矢下的表示：

# Rotation: C3z
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
    [0.0, 1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, 0.0],
])

# Rotation: C2z
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [0.0, 0.0, -1.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])

# Rotation: C2y
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, 0.0],
    [0.0, 0.0, 0.0, -1.0],
])

# Mirror: m_{1,-1,0}
mU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, 0.0],
    [0.0, 1.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])

View Code

运行Qsymm程序，可得：

一阶微扰 k 的一次项：

Matrix([[1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])
Matrix([[0, I*k_x, I*k_y, I*k_z], [-I*k_x, 0, 0, 0], [-I*k_y, 0, 0, 0], [-I*k_z, 0, 0, 0]])

不难发现，与 kp-method 书的 Chapter 4: 4.1 公式一致。

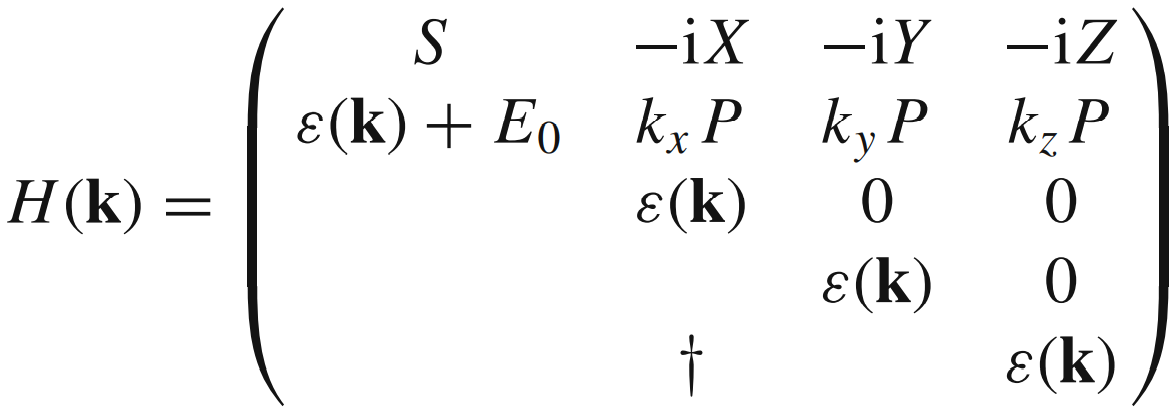
注意，该矩阵的所选基矢是 -iX, -iY, -iZ。

二阶微扰 k 的二次项:

Matrix([[1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])
Matrix([[0, I*k_x, I*k_y, I*k_z], [-I*k_x, 0, 0, 0], [-I*k_y, 0, 0, 0], [-I*k_z, 0, 0, 0]])
Matrix([[0, k_y*k_z, k_x*k_z, k_x*k_y], [k_y*k_z, 0, 0, 0], [k_x*k_z, 0, 0, 0], [k_x*k_y, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 0, k_x*k_y, k_x*k_z], [0, k_x*k_y, 0, k_y*k_z], [0, k_x*k_z, k_y*k_z, 0]])
Matrix([[k_x**2 + k_y**2 + k_z**2, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, k_x**2, 0, 0], [0, 0, k_y**2, 0], [0, 0, 0, k_z**2]])
Matrix([[0, 0, 0, 0], [0, k_y**2 + k_z**2, 0, 0], [0, 0, k_x**2 + k_z**2, 0], [0, 0, 0, k_x**2 + k_y**2]])

与书中 Table 4.2 一致。

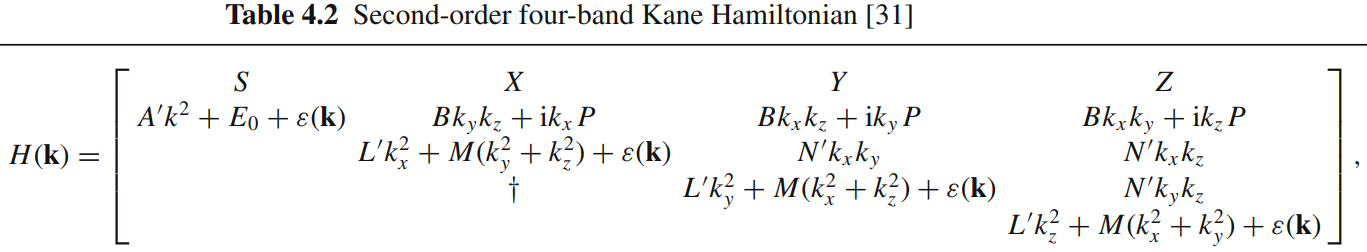
四带 Luttinger Model

import numpy as np
import sympy
import qsymm

# Spatial inversion
pU = np.array([
    [-1.0, 0.0, 0.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [0.0, 0.0, -1.0, 0.0],
    [0.0, 0.0, 0.0, -1.0],
])
pS = qsymm.inversion(3, U=pU)

# Time reversal
trU = np.array([
    [0.0, 0.0, 0.0, -1.0],
    [0.0, 0.0, 1.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [1.0, 0.0, 0.0, 0.0],
])
trS = qsymm.time_reversal(3, U=trU)

# Rotation
rotU = np.array([
    [0.25*(-1-1j), 0.25*np.sqrt(3)*(-1+1j), 0.25*np.sqrt(3)*(1+1j), 0.25*(1-1j)],
    [0.25*np.sqrt(3)*(-1-1j), 0.25*(-1+1j), 0.25*(-1-1j), 0.25*np.sqrt(3)*(-1+1j)],
    [0.25*np.sqrt(3)*(-1-1j), 0.25*(1-1j), 0.25*(-1-1j), 0.25*np.sqrt(3)*(1-1j)],
    [0.25*(-1-1j), 0.25*np.sqrt(3)*(1-1j), 0.25*np.sqrt(3)*(1+1j), 0.25*(-1+1j)],
])
C3zS = qsymm.rotation(1/3, [1,1,1], U=rotU)

# Rotation
rotU = np.array([
    [0.0, 0.0, 0.0, -1.0],
    [0.0, 0.0, 1.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [1.0, 0.0, 0.0, 0.0],
])
C2yS = qsymm.rotation(1/2, [0,1,0], U=rotU)

# # Rotation
# rotU = np.array([
#     [0.0, -1.0, 0.0],
#     [-1.0, 0.0, 0.0],
#     [0.0, 0.0, 1.0],
# ])
# C2xxS = qsymm.rotation(1/2, [1,1,0], U=rotU)

symmetries = [C3zS, C2yS, pS, trS]

dim = 3
total_power = 2

family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
qsymm.display_family(family)

DKK WZ 模型

import numpy as np
import sympy
import qsymm

# Time reversal
trU = np.diag([1, 1, 1])
trS = qsymm.time_reversal(3, U=trU)

rotU = np.array([
    [0.0, -1.0, 0.0],
    [1.0, -1.0, 0.0],
    [0.0, 0.0, 1.0],
])
C3zS = qsymm.rotation(1/3, [0,0,1], U=rotU)

rotU = np.array([
    [-1.0, 0.0, 0.0],
    [0.0, -1.0, 0.0],
    [0.0, 0.0, 1.0],
])
C2zS = qsymm.rotation(1/2, [0,0,1], U=rotU)

rotU = np.array([
    [0.0, -1.0, 0.0],
    [-1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0],
])
m110S = qsymm.mirror([1,1,0], U=rotU)

symmetries = [C3zS, C2zS, m110S, trS]
dim = 3
total_power = 2
family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
qsymm.display_family(family)

AO 哈密顿量

import numpy as np
import sympy
import qsymm

# Time reversal
trU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, 0.0],
    [0.0, 1.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
trS = qsymm.time_reversal(3, U=trU)

rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 1j-0.5, 0.5, 0.0],
    [0.0, 0.5, 0.5-1j, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
C3zS = qsymm.rotation(1/3, [0,0,1], U=rotU)

rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [0.0, 0.0, -1.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
C2zS = qsymm.rotation(1/2, [0,0,1], U=rotU)

rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 0.0, 1j, 0.0],
    [0.0, 1j, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
m110S = qsymm.mirror([1,1,0], U=rotU)

symmetries = [C3zS, C2zS, m110S, trS]
dim = 3
total_power = 2
family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
qsymm.display_family(family)

附录

附录1: 金刚石结构 DKK 哈密顿量 Qsymm 程序

import numpy as np
import sympy
import qsymm

# Spatial inversion
pU = np.array([
    [1.0, 0.0, 0.0],
    [0.0, 1.0, 0.0],
    [0.0, 0.0, 1.0]
])
pS = qsymm.inversion(3, U=pU)

# Time reversal
trU = np.diag([1, 1, 1])
trS = qsymm.time_reversal(3, U=trU)

# Rotation: C3z
rotU = np.array([
    [0.0, 0.0, 1.0],
    [1.0, 0.0, 0.0],
    [0.0, 1.0, 0.0],
])
C3zS = qsymm.rotation(1/3, [1,1,1], U=rotU)

# Rotation: C2y
rotU = np.array([
    [-1.0, 0.0, 0.0],
    [0.0, 1.0, 0.0],
    [0.0, 0.0, -1.0],
])
C2yS = qsymm.rotation(1/2, [0,1,0], U=rotU)

# Rotation: C2_110
rotU = np.array([
    [0.0, -1.0, 0.0],
    [-1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0],
])
C2xxS = qsymm.rotation(1/2, [1,1,0], U=rotU)

symmetries = [C3zS, C2yS, C2xxS, pS, trS]

dim = 3
total_power = 2

family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
qsymm.display_family(family)

### Ouput:
'''
Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
Matrix([[k_y**2 + k_z**2, 0, 0], [0, k_x**2 + k_z**2, 0], [0, 0, k_x**2 + k_y**2]])
Matrix([[k_x**2, 0, 0], [0, k_y**2, 0], [0, 0, k_z**2]])
Matrix([[0, k_x*k_y, k_x*k_z], [k_x*k_y, 0, k_y*k_z], [k_x*k_z, k_y*k_z, 0]])
'''

View Code

附录2: DKK 能带绘制

import numpy as np 
import matplotlib.pyplot as plt

def H(kx,ky,kz):
    H0, H1 = np.eye(3), np.eye(3)
    H0 = M*(kx**2+ky**2+kz**2)*H0
    H1[0][0],H1[0][1],H1[0][2] = (L-M)*kx**2, N*kx*ky, N*kx*kz
    H1[1][0],H1[1][1],H1[1][2] = N*kx*ky, (L-M)*ky**2, N*ky*kz
    H1[2][0],H1[2][1],H1[2][2] = N*kx*kz, N*ky*kz,  (L-M)*kz**2
    return H0+H1

def plot1():
    res1,res2,res3 = [],[],[]

    kpath = [0]
    Lp = [0.5*1.1491,0.5*1.1491,0.5*1.1491]
    Lp = [1.1491,1.1491,1.1491]
    len_L = 100
    kxold,kyold,kzold = 0,0,0
    for i in range(len_L-1,-1,-1):
        kx = i*Lp[0]/(len_L-1)
        ky = i*Lp[1]/(len_L-1)
        kz = i*Lp[2]/(len_L-1)
        tmp = kpath[-1] + ((kx-kxold)**2+(ky-kyold)**2+(kz-kzold)**2)**0.5
        kpath.append(tmp)
        kxold,kyold,kzold = kx,ky,kz

        a, b = np.linalg.eig(H(kx,ky,kz))
        a = sorted(a)
        res1.append(a[0])
        res2.append(a[1])
        res3.append(a[2])
    
    flag = kpath[-1]
    
    Xp = [1.1491*2,0,0]
    len_X = 100
    kxold,kyold,kzold = 0,0,0
    for i in range(len_X):
        kx = i*Xp[0]/(len_L-1)
        ky = i*Xp[1]/(len_L-1)
        kz = i*Xp[2]/(len_L-1)
        tmp = kpath[-1] + ((kx-kxold)**2+(ky-kyold)**2+(kz-kzold)**2)**0.5
        kpath.append(tmp)
        kxold,kyold,kzold = kx,ky,kz

        a, b = np.linalg.eig(H(kx,ky,kz))
        a = sorted(a)
        res1.append(a[0])
        res2.append(a[1])
        res3.append(a[2])

    plt.plot(kpath[1:],res1)
    plt.plot(kpath[1:],res2)
    plt.plot(kpath[1:],res3)
    plt.axvline(flag)
    # plt.ylim([-40,0])
    plt.ylim([-150,0])
    plt.show()

if __name__ == '__main__':
    L = -1.9
    M = -6.7
    N = -7.5

    L = -31.8
    M = -5.1
    N = -32.1

    plot1()

View Code

附录3: 闪锌矿结构四带 Kane 模型

import numpy as np
import sympy
import qsymm

# Time reversal
trU = np.diag([1, 1, 1, 1])
trS = qsymm.time_reversal(3, U=trU)

# Rotation: C3z
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
    [0.0, 1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, 0.0],
])
C3zS = qsymm.rotation(1/3, [1,1,1], U=rotU)

# Rotation: C2z
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [0.0, 0.0, -1.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
C2zS = qsymm.rotation(1/2, [0,0,1], U=rotU)

# Rotation: C2y
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, 0.0],
    [0.0, 0.0, 0.0, -1.0],
])
C2yS = qsymm.rotation(1/2, [0,1,0], U=rotU)

# Mirror: m_{1,-1,0}
mU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, 0.0],
    [0.0, 1.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
MxS = qsymm.mirror([1,-1,0], U=mU)
symmetries = [C3zS, C2zS, C2yS, MxS, trS]

dim = 3
total_power = 2

family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
qsymm.display_family(family)

### Output
'''
To the Order 1:
Matrix([[1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])
Matrix([[0, I*k_x, I*k_y, I*k_z], [-I*k_x, 0, 0, 0], [-I*k_y, 0, 0, 0], [-I*k_z, 0, 0, 0]])

To the Order 2:
Matrix([[1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])
Matrix([[0, I*k_x, I*k_y, I*k_z], [-I*k_x, 0, 0, 0], [-I*k_y, 0, 0, 0], [-I*k_z, 0, 0, 0]])
Matrix([[0, k_y*k_z, k_x*k_z, k_x*k_y], [k_y*k_z, 0, 0, 0], [k_x*k_z, 0, 0, 0], [k_x*k_y, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 0, k_x*k_y, k_x*k_z], [0, k_x*k_y, 0, k_y*k_z], [0, k_x*k_z, k_y*k_z, 0]])
Matrix([[k_x**2 + k_y**2 + k_z**2, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, k_x**2, 0, 0], [0, 0, k_y**2, 0], [0, 0, 0, k_z**2]])
Matrix([[0, 0, 0, 0], [0, k_y**2 + k_z**2, 0, 0], [0, 0, k_x**2 + k_z**2, 0], [0, 0, 0, k_x**2 + k_y**2]])
'''

View Code

附录5: 纤锌矿结构四带 AO 模型

### Andreev-O' Reilly for Wurtzite
import numpy as np
import sympy
import qsymm

# Time reversal
trU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 0.0, 1.0, 0.0],
    [0.0, 1.0, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
trS = qsymm.time_reversal(3, U=trU)

# C3z
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 1j-0.5, 0.5, 0.0],
    [0.0, 0.5, -0.5-1j, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
C3zS = qsymm.rotation(1/3, [0,0,1], U=rotU)

# C2z
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, -1.0, 0.0, 0.0],
    [0.0, 0.0, -1.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
C2zS = qsymm.rotation(1/2, [0,0,1], U=rotU)

# m110
rotU = np.array([
    [1.0, 0.0, 0.0, 0.0],
    [0.0, 0.0, 1j, 0.0],
    [0.0, -1j, 0.0, 0.0],
    [0.0, 0.0, 0.0, 1.0],
])
m110S = qsymm.mirror([1,1,0], U=rotU)

symmetries = [C3zS, C2zS, m110S, trS]
dim = 3
total_power = 1
family = qsymm.continuum_hamiltonian(symmetries, dim, total_power, prettify=True)
qsymm.display_family(family)

#### Output
'''
Matrix([[1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 1], [0, 0, 0, 0], [0, 0, 0, 0], [1, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 1, I/2, 0], [0, -I/2, 1, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 1]])
Matrix([[0, 0, 0, I*k_z], [0, 0, 0, 0], [0, 0, 0, 0], [-I*k_z, 0, 0, 0]])
Matrix([[0, k_x*(1 + 669872981*I/2500000000) + k_y*(-669872981/2500000000 - I), k_x*(-1 + 669872981*I/2500000000) + k_y*(669872981/2500000000 - I), 0], [k_x*(1 - 669872981*I/2500000000) + k_y*(-669872981/2500000000 + I), 0, 0, 0], [k_x*(-1 - 669872981*I/2500000000) + k_y*(669872981/2500000000 + I), 0, 0, 0], [0, 0, 0, 0]])
Matrix([[0, 0, 0, 0], [0, 0, 0, k_x*(1 - 669872981*I/2500000000) + k_y*(-669872981/2500000000 + I)], [0, 0, 0, k_x*(-1 - 669872981*I/2500000000) + k_y*(669872981/2500000000 + I)], [0, k_x*(1 + 669872981*I/2500000000) + k_y*(-669872981/2500000000 - I), k_x*(-1 + 669872981*I/2500000000) + k_y*(669872981/2500000000 - I), 0]])
'''

View Code

posted @ 2022-09-05 19:50 ghzphy 阅读(1756) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· Qsymm 和 kdotp_symmetry 对比

· The k·p Hamiltonian of graphene

· CKKS Part2: CKKS的编码和解码

· 量子机器学习教程-全-

· SciPy-1-12-中文文档-八-

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列01：轻松3步本地部署deepseek，普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现

公告

昵称： ghzphy
园龄： 4年10个月
粉丝： 55
关注： 1

+加关注

2025年3月

日

一

二

三

四

五

六

ghzhan

常见的半导体 k·p 哈密顿量

公告

搜索

常用链接

我的标签

随笔分类

随笔档案

文章分类

阅读排行榜

评论排行榜

推荐排行榜

最新评论