Dirac源晶体管亚阈值摆幅推导

背景

亚阈值摆幅

亚阈值摆幅 (Subthrehold Swing) 是衡量晶体管开启与关断状态之间相互转换速率的性能指标，它代表源漏电流变化十倍所需要栅电压的变化量，又称为S因子，S越小意味着开启关断速率ON/OFF越快。 (来源: 百度百科)

S S = \frac{d V_{g s}}{d l o g I_{d s}} = \frac{d V_{g s}}{d V_{s}} * \frac{d V_{s}}{d l o g I_{d s}} = \frac{k_{B} T l n 10}{q} * \frac{d V_{g s}}{d V_{s}}

$SS = \frac{dV_{gs}}{d \mathbf{log} I_{ds}} = \frac{dV_{gs}}{dV_s}* \frac{dV_s}{d \mathbf{log} I_{ds}}=\frac{k_BTln10}{q}* \frac{dV_{gs}}{dV_s}$

因为加在栅极的电压 $V_{gs}$ 分别降落在栅氧化蹭和衬底硅上，所以 $V_{gs} >= V_s$ , $\frac{dV_{gs}}{dV_s}>=1$ , 在室温下 (300K), SS 有最小值 $k_BT/q * ln10\approx 60 mV$ . 因此，对于常规的 MOSFET 而言，亚阈值摆幅一般大于 60 mV/dec。但一些新型器件，如隧穿器件（Tunneling Transistor），可以获得低于此理论值的亚阈值摆幅。

Dirac 源晶体管

简介

2018年，北京大学刘飞老师等人提出用 Dirac 材料作为源端的晶体管，可以打破亚阈值摆幅 60 $mV/dec$ 的下限，实现更低功耗的作用。本文主要是推导 IEEE TED 65,7 (2018) 的 $SS$ 值。

图来源自 Nano Lett. 21, 1758 (2021).

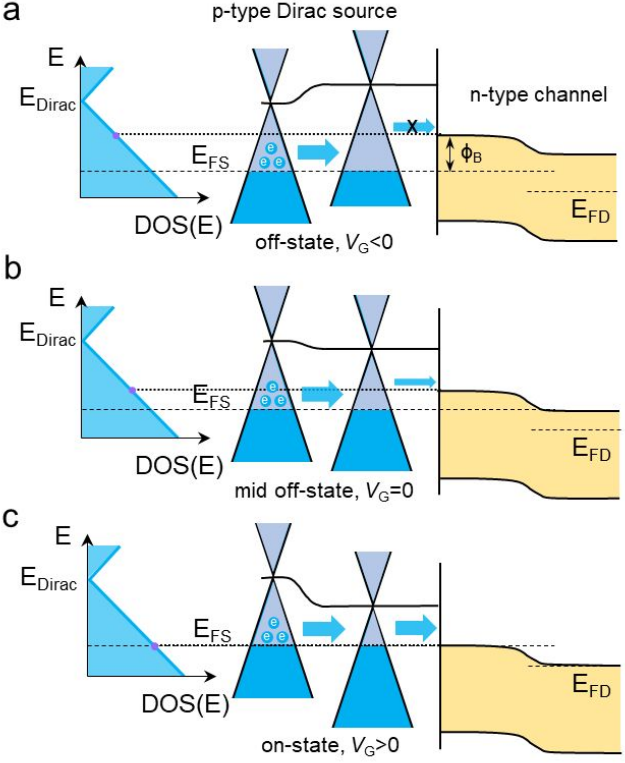
根据 Landauer-Buttiker 公式, 通过器件的电流为:

I = \frac{2 q}{h} \int D (E) T (E) [f_{S} - f_{D}] d E

$I = \frac{2q}{h}\int D(E)T(E)[f_S-f_D]dE$

这里的 $D(E)$ 是注入载流子的态密度， $f_S/f_D$ 是源漏电极的费米能级， $T(E)$ 是源端到漏端的隧穿概率。在常规的MOSFET中，源端是通过金属载流子注入，所以它的态密度是个常数，因此， $SS$ 存在一个极限 $k_BT/q * ln10$ ，然而当栅压减小时，态密度如果出现急剧下降的话，则 $SS$ 将打破热力学极限。

对于某种材料，带边附近的电子色散关系为:

E = E_{c / v} \pm c_{o} k^{m}

$E=E_{c/v}\pm c_ok^m$

这里的 $E_{c/v}$ 分别表示导带价带的带边能量。当 m = 2 表示有质量，m=1 表示 Dirac 电子，因此， $d$ -维材料的态密度有如下关系:

D (E) = D_{0} | E - E_{c / v} |^{d / m - 1}

$D(E)=D_0|E-E_{c/v}|^{d/m-1}$

$\frac{d}{m}-1$ 的值为:

d/m-1	m=2	m=1
d=1	-1/2	0
d=2	0	1
d=3	1/2	2

详细推导

1. $\frac{d}{m}-1 = 0$ 例子

态密度为 $D(E)=D_0|E-E_{dirac}|^0=D_0$ ，电流值为:

I_{t h e r m a l} \approx \frac{2 q}{h} D_{0} \int_{Φ_{B}}^{+ \infty} e^{- E / k_{B} T} d E = k_{B} T e^{- Φ_{B} / k_{B} T}

$I_{thermal}\approx\frac{2q}{h}D_0\int^{+\infty}_{\Phi_B} e^{-E/k_BT}dE=k_BTe^{-\Phi_B/k_BT}$

S S = \frac{d V_{g s}}{d l o g 10 I_{t h e r m a l}} = l n 10 \frac{d V_{g s}}{d Φ_{B}} / \frac{d l n I_{t h e r m a l}}{d Φ_{B}} = \frac{k_{B} T l n 10}{q} \frac{1}{C_{1}}

$SS=\frac{dV_{gs}}{d \mathbf{log10} I_{thermal}}=ln10\frac{dV_{gs}}{d\Phi_B}/\frac{d \mathbf{ln} I_{thermal}}{d\Phi_B}=\frac{k_BTln10}{q}\frac{1}{C_1}$

这里的 $C_1=-\frac{\partial\Phi_B}{\partial qV_{gs}} （0 < C_1 <=1）$

2. $\frac{d}{m}-1 = 1$ 例子

当源端是二维石墨烯 Dirac 材料时，d = 2，m =1, 那么 $\frac{d}{m}-1 = 1$ 。那么它的态密度为 $D(E)=D_0|E-E_{dirac}|$ 电流值为:

I_{t h e r m a l} = \frac{2 q}{h} D_{0} \int_{Φ_{B}}^{+ \infty} d E T (E) | E - E_{d i r a c} | [f_{S} - f_{D}]

$I_{thermal}=\frac{2q}{h}D_0\int^{+\infty}_{\Phi_B}dE T(E)|E-E_{dirac}|[f_S-f_D]$

\approx \frac{2 q}{h} D_{0} \int_{Φ_{B}}^{+ \infty} d E | E - E_{d i r a c} | e^{- E / k_{B} T}

$\approx\frac{2q}{h}D_0\int^{+\infty}_{\Phi_B}dE |E-E_{dirac}|e^{-E/k_BT}$

这里假设 $T(E)=1$ , 源端费米能级为 $E_{FS}=0$ ，当 $\Phi_B$ 大于 $E_{dirac}$ 时， $|E-E_{dirac}| = E-E_{dirac}$ ，电流值为

I_{t h e r m a l} = \frac{2 q}{h} D_{0} * (k_{B} T Φ_{B} - k_{B} T E_{d i r a c} + (k_{B} T)^{2}) e^{- Φ_{B} / k_{B} T}

$I_{thermal}=\frac{2q}{h}D_0*(k_BT\Phi_B-k_BTE_{dirac}+(k_BT)^2)e^{-\Phi_B/k_BT}$

= \frac{2 q}{h} D_{0} k_{B} T * (Φ_{B} - E_{d i r a c} + k_{B} T) e^{- Φ_{B} / k_{B} T}

$=\frac{2q}{h}D_0k_BT*(\Phi_B-E_{dirac}+k_BT)e^{-\Phi_B/k_BT}$

因此 SS 值为:

S S = \frac{d V_{g s}}{d l o g 10 I_{t h e r m a l}} = \frac{k_{B} T l n 10}{q} \frac{1}{C_{1}} (1 + \frac{k_{B} T}{Φ_{B} - E_{d i r a c}})

$SS=\frac{dV_{gs}}{d \mathbf{log10} I_{thermal}}=\frac{k_BTln10}{q}\frac{1}{C_1}\left(1+\frac{k_BT}{\Phi_B-E_{dirac}}\right)$

当 $\Phi_B$ 小于 $E_{dirac}$ 时， $|E-E_{dirac}|$ 分情况讨论, 电流值为

I_{t h e r m a l} == \int_{Φ_{B}}^{+ \infty} d E = \int_{E_{d i r a c}}^{+ \infty} d E + \int_{Φ_{B}}^{E_{d i r a c}} d E

$I_{thermal} == \int^{+\infty}_{\Phi_B}dE = \int^{+\infty}_{E_{dirac}}dE + \int^{E_{dirac}}_{\Phi_B}dE$

== \int_{E_{d i r a c}}^{+ \infty} (E - E_{d i r a c}) e^{- E / k_{B} T} d E + \int_{Φ_{B}}^{E_{d i r a c}} (E_{d i r a c} - E) e^{- E / k_{B} T} d E

$==\int^{+\infty}_{E_{dirac}}(E-E_{dirac})e^{-E/k_BT}dE + \int^{E_{dirac}}_{\Phi_B}(E_{dirac}-E)e^{-E/k_BT}dE$

= 2 * \frac{2 q}{h} D_{0} (k_{B} T)^{2} e^{- E_{d i r a c} / k_{B} T} - \frac{2 q}{h} D_{0} (k_{B} T Φ_{B} - k_{B} T E_{d i r a c} + (k_{B} T)^{2}) e^{- Φ_{B} / k_{B} T}

$=2*\frac{2q}{h}D_0(k_BT)^2e^{-E_{dirac}/k_BT}-\frac{2q}{h}D_0(k_BT\Phi_B-k_BTE_{dirac}+(k_BT)^2)e^{-\Phi_B/k_BT}$

= \frac{2 q}{h} D_{0} k_{B} T (2 k_{B} T * e^{- E_{d i r a c} / k_{B} T} + (E_{d i r a c} - Φ_{B} - k_{B} T) e^{- Φ_{B} / k_{B} T})

$=\frac{2q}{h}D_0k_BT(2k_BT*e^{-E_{dirac}/k_BT}+(E_{dirac}-\Phi_B-k_BT)e^{-\Phi_B/k_BT})$

3. $\frac{d}{m}-1 = 2$ 例子

态密度 $|E-E_{dirac}|^2 = (E-E_{dirac})^2$ ，电流值为

I_{t h e r m a l} \approx \frac{2 q}{h} D_{0} \int_{Φ_{B}}^{+ \infty} d E | E - E_{d i r a c} |^{2} e^{- E / k_{B} T}

$I_{thermal}\approx\frac{2q}{h}D_0\int^{+\infty}_{\Phi_B}dE |E-E_{dirac}|^2e^{-E/k_BT}$

= \frac{2 q}{h} D_{0} (a Φ_{B}^{2} + (2 a^{2} - 2 a b) Φ_{B} + a b^{2} - 2 a^{2} b + 2 a^{3}) e^{- Φ_{B} / k_{B} T}

$=\frac{2q}{h}D_0(a\Phi_B^2+(2a^2-2ab)\Phi_B+ab^2-2a^2b+2a^3)e^{-\Phi_B/k_BT}$

其中 $a=k_BT,b=E_{dirac}$

4. $\frac{d}{m}-1 = 1/2$ 例子

当 $\Phi_B$ 大于 $E_{dirac}$ 时， $|E-E_{dirac}|^{1/2} = \sqrt{E-E_{dirac}}$ ，电流值为

I_{t h e r m a l} \approx \frac{2 q}{h} D_{0} \int_{Φ_{B}}^{+ \infty} d E \sqrt{E - E_{d i r a c}} e^{- E / k_{B} T}

$I_{thermal}\approx\frac{2q}{h}D_0\int^{+\infty}_{\Phi_B}dE \sqrt{E-E_{dirac}}e^{-E/k_BT}$

当 $\Phi_B$ 小于 $E_{dirac}$ 时， $|E-E_{dirac}|^{1/2} = \sqrt{E_{dirac}-E}$ ，电流值为

I_{t h e r m a l} \approx \frac{2 q}{h} D_{0} \int_{Φ_{B}}^{+ \infty} d E \sqrt{E_{d i r a c} - E} e^{- E / k_{B} T}

$I_{thermal}\approx\frac{2q}{h}D_0\int^{+\infty}_{\Phi_B}dE \sqrt{E_{dirac}-E}e^{-E/k_BT}$

5. $\frac{d}{m}-1 = -1/2$ 例子

当 $\Phi_B$ 大于 $E_{dirac}$ 时， $|E-E_{dirac}|^{-1/2} = (E-E_{dirac})^{-1/2}$ ，电流值为

I_{t h e r m a l} \approx \frac{2 q}{h} D_{0} \int_{Φ_{B}}^{+ \infty} d E (E - E_{d i r a c})^{- 1 / 2} e^{- E / k_{B} T}

$I_{thermal}\approx\frac{2q}{h}D_0\int^{+\infty}_{\Phi_B}dE (E-E_{dirac})^{-1/2}e^{-E/k_BT}$

= \frac{2 q}{h} D_{0} \sqrt{π} (k_{B} T)^{1 / 2} e^{- \frac{E_{d i r a c}}{k_{B} T}} e r f (\sqrt{\frac{Φ_{B} - E_{d i r a c}}{k_{B} T}})

$=\frac{2q}{h}D_0\sqrt{\pi}(k_BT)^{1/2}e^{-\frac{E_{dirac}}{k_BT}}\mathbf{erf}(\sqrt{\frac{\Phi_B-E_{dirac}}{k_BT}})$

当 $\Phi_B$ 小于 $E_{dirac}$ 时， $|E-E_{dirac}|^{-1/2}$ 分情况讨论，电流值为

I_{t h e r m a l} == \int_{Φ_{B}}^{+ \infty} d E = \int_{E_{d i r a c}}^{+ \infty} d E + \int_{Φ_{B}}^{E_{d i r a c}} d E

$I_{thermal} == \int^{+\infty}_{\Phi_B}dE = \int^{+\infty}_{E_{dirac}}dE + \int^{E_{dirac}}_{\Phi_B}dE$

== \int_{E_{d i r a c}}^{+ \infty} (E - E_{d i r a c})^{- 1 / 2} e^{- E / k_{B} T} d E + \int_{Φ_{B}}^{E_{d i r a c}} (E_{d i r a c} - E)^{- 1 / 2} e^{- E / k_{B} T} d E

$==\int^{+\infty}_{E_{dirac}}(E-E_{dirac})^{-1/2}e^{-E/k_BT}dE + \int^{E_{dirac}}_{\Phi_B}(E_{dirac}-E)^{-1/2}e^{-E/k_BT}dE$

附录积分公式 (参考链接)

$\int (x-b)^0e^{-x/a}dx = -ae^{-x/a}$
$\int (x-b)e^{-x/a}dx = -(ax-ab+a^2)e^{-x/a}$

\int (b - x) e^{- x / a} d x = (a x - a b + a^{2}) e^{- x / a}

$\int (b-x)e^{-x/a}dx = (ax-ab+a^2)e^{-x/a}$

$\int (x-b)^2e^{-x/a}dx = -(ax^2+(2a^2-2ab)x+ab^2-2a^2b+2a^3)e^{-x/a}$
$\int (x-b)^{1/2}e^{-x/a}dx = -\frac{1}{2}*e^{-\frac{x+b}{a}}\left(2ae^{\frac{b}{a}}\sqrt{x-b}-\sqrt{\pi}a^{3/2}e^{\frac{x}{a}} \mathbf{erf}(\sqrt{\frac{x-b}{a}})\right)$

\int (b - x)^{1 / 2} e^{- x / a} d x = - \frac{1}{2} * e^{- \frac{x + b}{a}} (2 a e^{\frac{b}{a}} \sqrt{b - x} + i \sqrt{π} a^{3 / 2} e^{\frac{x}{a}} e r f (i \sqrt{\frac{b - x}{a}}))

$\int (b-x)^{1/2}e^{-x/a}dx = -\frac{1}{2}*e^{-\frac{x+b}{a}}\left(2ae^{\frac{b}{a}}\sqrt{b-x}+i\sqrt{\pi}a^{3/2}e^{\frac{x}{a}} \mathbf{erf}(i\sqrt{\frac{b-x}{a}})\right)$

这里的 $\mathbf{erf}$ 是误差函数:

e r f (x) = \frac{2}{\sqrt{π}} \int_{0}^{x} e^{- y^{2}} d y .

$erf(x)=\frac{2}{\sqrt{\pi}}\int^{x}_0 e^{-y^2} dy.$

所以 $\mathbf{erf}(0)=0,\mathbf{erf}(\infty)=1$ 且 $i\mathbf{erf}(ix)=-\mathbf{erf}(x)$ .

$\int (x-b)^{-1/2}e^{-x/a}dx = \sqrt{\pi}a^{1/2}e^{-\frac{b}{a}}\mathbf{erf}(\sqrt{\frac{x-b}{a}})$

\int (b - x)^{- 1 / 2} e^{- x / a} d x = i \sqrt{π} a^{1 / 2} e^{- \frac{b}{a}} e r f (i \sqrt{\frac{b - x}{a}})

$\int (b-x)^{-1/2}e^{-x/a}dx = i\sqrt{\pi}a^{1/2}e^{-\frac{b}{a}}\mathbf{erf}(i\sqrt{\frac{b-x}{a}})$

Python 计算脚本

$D(E)=D_0|E-E_{dirac}|^0$ 例子

点击查看代码

import numpy as np 
import matplotlib.pyplot as plt
import math

def current1(phi_b):
	tmp = math.exp(-phi_b/KT)
	return math.log(KT*tmp)

def current2(phi_b):
	tmp = math.exp(-phi_b/KT)
	return math.log(KT*tmp)

def derivative(f,x,deltax=0.1**10):
	return (f(x+deltax)-f(x))/deltax

def main():
	phiB = np.linspace(0,0.6,2000)
	phi_B, SS = [], []
	for i in phiB:
		if i > E_dirac:
			phi_B.append(i)
			SS.append(-60/(KT*derivative(current1,i)))
		elif i < E_dirac:
			phi_B.append(i)
			SS.append(-60/(KT*derivative(current2,i)))

	plt.plot(phi_B,SS)
	plt.xlim([0,0.6])
	plt.ylim([0,200])
	plt.title('$D(E) \\approx |E-E_{dirac}|^0$')
	plt.show()

if __name__ == '__main__': 
	KT = 0.026
	E_dirac = 0.3
	main()

$D(E)=D_0|E-E_{dirac}|$ 例子

点击查看代码

import numpy as np 
import matplotlib.pyplot as plt
import math

def current1(phi_b):
	tmp = (phi_b + KT -E_dirac)*math.exp(-phi_b/KT)
	return math.log(KT*tmp)

def current2(phi_b):
	tmp = 2*KT*math.exp(-E_dirac/KT) + (-phi_b - KT +E_dirac)*math.exp(-phi_b/KT)
	return math.log(KT*tmp)

def derivative(f,x,deltax=0.1**10):
	return (f(x+deltax)-f(x))/deltax

def main():
	phiB = np.linspace(0,0.6,2000)
	phi_B,SS = [],[]
	for i in phiB:
		if i > E_dirac:
			phi_B.append(i)
			SS.append(-60/(KT*derivative(current1,i)))
		elif i < E_dirac:
			phi_B.append(i)
			SS.append(-60/(KT*derivative(current2,i)))

	plt.plot(phi_B,SS)
	plt.xlim([0,0.6])
	plt.ylim([0,200])
	plt.title('$D(E) \\approx |E-E_{dirac}|$')
	plt.show()

if __name__ == '__main__':
	KT = 0.026
	E_dirac = 0.3
	main()

$D(E)=D_0|E-E_{dirac}|^2$ 例子

点击查看代码

import numpy as np 
import matplotlib.pyplot as plt
import math

def current(x):
	# tmp = (2*(phi_b-E_dirac)*(KT)**2 + 2*(KT)**3 + KT*(phi_b-E_dirac)**2)*math.exp(-phi_b/KT)
	tmp = (a*x**2+(2*a**2-2*a*b)*x+a*b**2-2*a**2*b+2*a**3)*math.exp(-x/a)
	return math.log(tmp)

def derivative(f,x,deltax=0.1**10):
	return (f(x+deltax)-f(x))/deltax

def main():
	phiB = np.linspace(0,0.6,2000)
	phi_B,SS = [],[]
	for i in phiB:
		phi_B.append(i)
		SS.append(-60/(KT*derivative(current,i)))

	with open('dat.txt','w') as f:
		for i in range(len(phi_B)):
			f.write('{}  {}\n'.format(phi_B[i],SS[i]))

	plt.plot(phi_B,SS)
	plt.xlim([0,0.6])
	plt.ylim([0,200])
	plt.title('$D(E) \\approx |E-E_{dirac}|^2$')
	plt.show()

if __name__ == '__main__':
	KT = 0.026
	E_dirac = 0.3
	a = KT
	b = E_dirac
	main()

$D(E)=D_0|E-E_{dirac}|^{1/2}$ 例子

点击查看代码

import numpy as np 
import matplotlib.pyplot as plt
import math

def current1(phi_b):
	tmp1 = math.exp(-(phi_b+b)/a)
	tmp2 = ((phi_b-b)/a)**0.5
	tmp = math.pi**0.5*a**1.5*math.exp(-b/a) +tmp1*(2*a*math.exp(b/a)*(phi_b-b)**0.5 - math.pi**0.5*a**1.5*math.exp(phi_b/a)*math.erf(tmp2))
	return math.log(tmp/2)

def current2(phi_b):
	tmp1 = math.exp(-(phi_b+b)/a)
	tmp2 = ((b-phi_b)/a)**0.5
	tmp = math.pi**0.5*a**1.5*math.exp(-b/a) +tmp1*(2*a*math.exp(b/a)*(b-phi_b)**0.5 - math.pi**0.5*a**1.5*math.exp(phi_b/a)*math.erf(tmp2))
	return math.log(tmp/2)

def derivative(f,x,deltax=0.1**10):
	return (f(x+deltax)-f(x))/deltax

def main():
	phiB = np.linspace(0,0.6,2000)
	phi_B,SS = [],[]
	for i in phiB:
		if i > E_dirac:
			phi_B.append(i)
			SS.append(-60/(KT*derivative(current1,i)))
		elif i < E_dirac:
			phi_B.append(i)
			SS.append(-60/(KT*derivative(current2,i)))

	plt.figure()
	plt.plot(phi_B,SS)
	plt.ylim([0,200])
	plt.title('$D(E) \\approx |E-E_{dirac}|^{1/2}$')
	plt.xlim([0,0.6])
	plt.show()

if __name__ == '__main__':
	KT = 0.026
	E_dirac = 0.3
	b = E_dirac
	a = KT
	main()

$D(E)=D_0|E-E_{dirac}|^{-1/2}$ 例子

点击查看代码

import numpy as np 
import matplotlib.pyplot as plt
import math

def current1(phi_b):
	tmp1 = (a*math.pi)**0.5*math.exp(-b/a)
	tmp2 = ((phi_b-b)/a)**0.5
	tmp = tmp1-tmp1*math.erf(tmp2)
	return math.log(tmp)

def current2(phi_b):
	tmp1 = (a*math.pi)**0.5*math.exp(-b/a)
	tmp2 = ((b-phi_b)/a)**0.5
	tmp = tmp1+tmp1*math.erf(tmp2)
	return math.log(tmp)

def derivative(f,x,deltax=0.1**10):
	return (f(x+deltax)-f(x))/deltax


def main():
	phiB = np.linspace(0,0.6,2000)
	phi_B,SS = [],[]
	for i in phiB:
		if i > E_dirac:
			phi_B.append(i)
			SS.append(-60/(KT*derivative(current1,i)))
		elif i < E_dirac:
			phi_B.append(i)
			SS.append(-60/(KT*derivative(current2,i)))

	plt.figure()
	plt.plot(phi_B,SS)
	plt.xlim([0,0.6])
	plt.ylim([0,200])
	plt.title('$D(E) \\approx |E-E_{dirac}|^{-1/2}$')
	plt.show()

if __name__ == '__main__':
	KT = 0.026
	E_dirac = 0.3
	b = E_dirac
	a = KT
	main()

部分推导笔记

posted @ 2022-07-16 22:56 ghzphy 阅读(3136) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· Current of 2D Cross-Section/1D Cross-Section

· 常用物理常数

· 阅读报告 Phys. Rev. Lett. 130, 177001 (2023).

· 模拟集成电路设计系列博客——2.2.3 折叠Cascode放大器的摆率

· 《gm/ID设计法基本介绍》翻译

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列01：轻松3步本地部署deepseek，普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现

公告

昵称： ghzphy
园龄： 4年10个月
粉丝： 55
关注： 1

+加关注

2025年3月

日

一

二

三

四

五

六

ghzhan

Dirac源晶体管亚阈值摆幅推导

背景

亚阈值摆幅

Dirac 源晶体管

简介

详细推导

1. $\frac{d}{m}-1 = 0$ 例子

2. $\frac{d}{m}-1 = 1$ 例子

3. $\frac{d}{m}-1 = 2$ 例子

4. $\frac{d}{m}-1 = 1/2$ 例子

5. $\frac{d}{m}-1 = -1/2$ 例子

附录积分公式 (参考链接)

Python 计算脚本

公告

搜索

常用链接

我的标签

随笔分类

随笔档案

文章分类

阅读排行榜

评论排行榜

推荐排行榜

最新评论

背景

亚阈值摆幅

Dirac 源晶体管

简介

详细推导

1. dm−1=0dm−1=0\frac{d}{m}-1 = 0 例子

2. dm−1=1dm−1=1\frac{d}{m}-1 = 1 例子

3. dm−1=2dm−1=2\frac{d}{m}-1 = 2 例子

4. dm−1=1/2dm−1=1/2\frac{d}{m}-1 = 1/2 例子

5. dm−1=−1/2dm−1=−1/2\frac{d}{m}-1 = -1/2 例子

附录积分公式 (参考链接)

Python 计算脚本

公告

搜索

常用链接

随笔档案

1. $\frac{d}{m}-1 = 0$ 例子

2. $\frac{d}{m}-1 = 1$ 例子

3. $\frac{d}{m}-1 = 2$ 例子

4. $\frac{d}{m}-1 = 1/2$ 例子

5. $\frac{d}{m}-1 = -1/2$ 例子