空间群

本文是博主2019年10月的笔记，在此重新记录一遍。

 

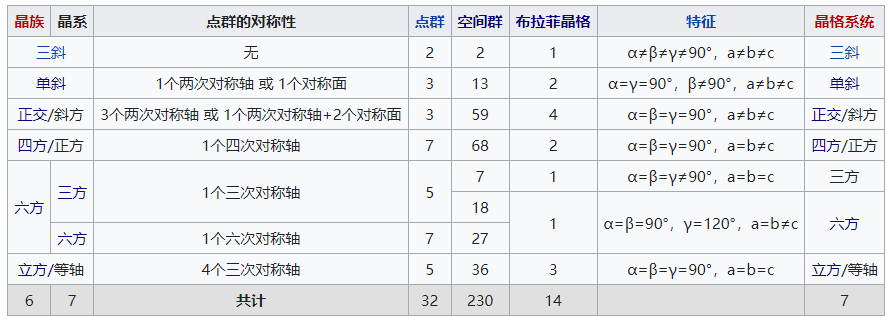
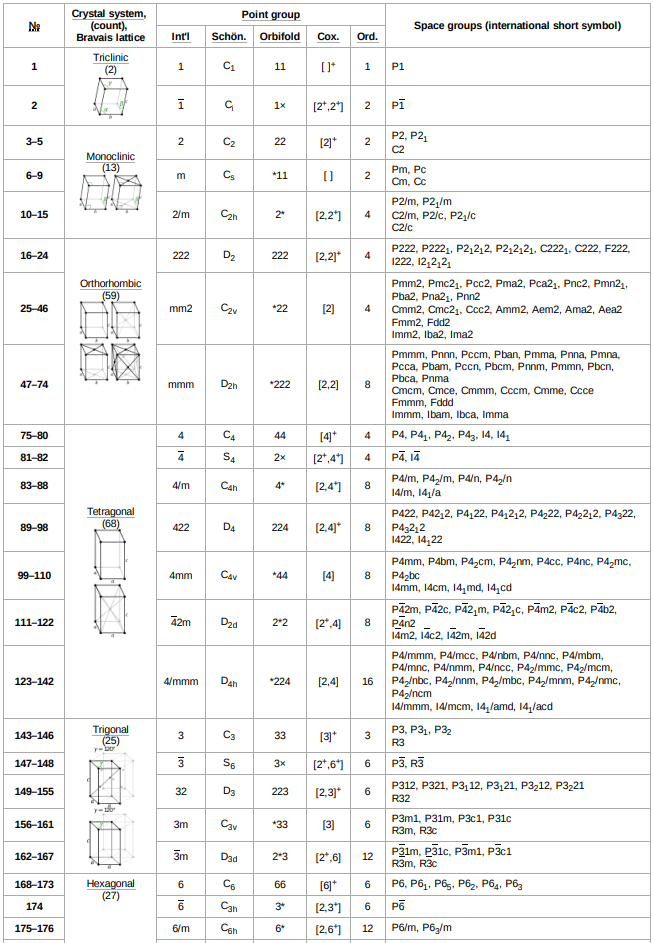
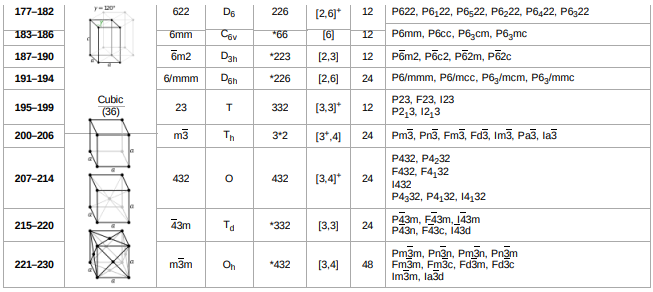
三维空间有230个空间群，32个点群，14种布拉菲格子，7大晶系。

1）三斜晶系 (Triclinic)

2）单斜晶系 (Monoclinic)

3）正交晶系 (Orthorhombic)

4）四方晶系 (Tetragonal)

5）三方晶系 (Trigonal)

6）六方晶系 (Hexagonal)

7）立方晶系 (Cubic)

 

Crystal system - Wikipedia

 

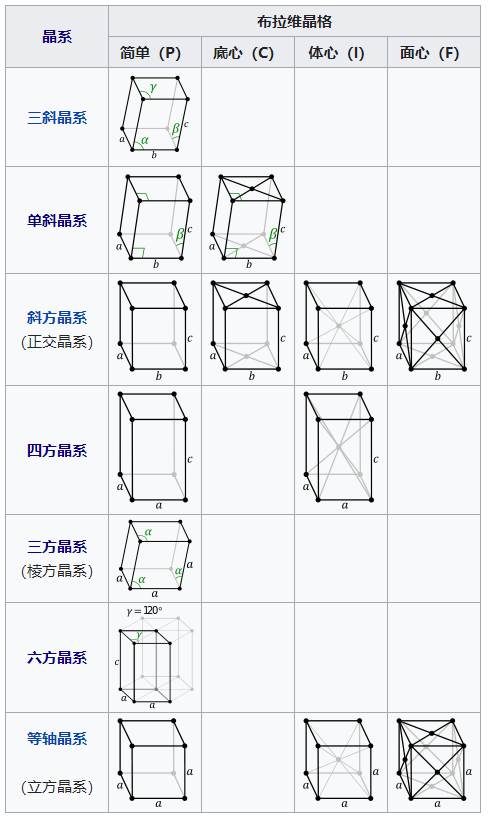
布拉菲格子

 

 

32个点群

Due to the crystallographic restriction theorem, n = 1, 2, 3, 4, or 6 in 2- or 3-dimensional space.

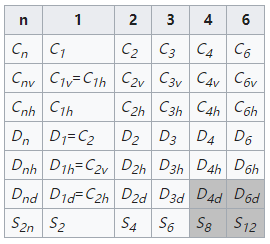
D_4d and D_6d are actually forbidden because they contain improper rotations with n=8 and 12 respectively. The 27 point groups in the table plus T, T_d, T_h, O and O_h constitute 32 crystallographic point groups.

Crystallographic point group - Wikipedia

 

230个空间群

 

 

对称操作

 

 

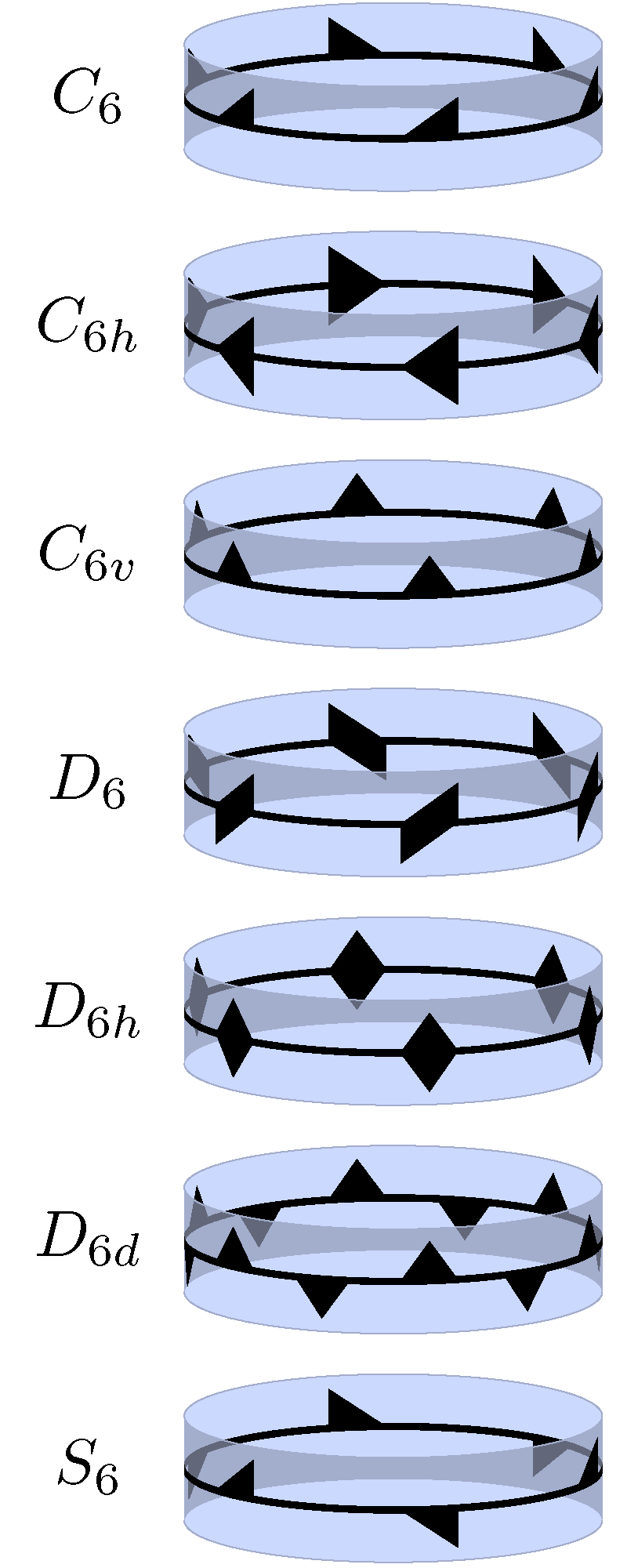
Point Groups

If two symmetry operations are symmetry elements of an object, then their product is also a symmetry element. Any set of operations for which any product of members of that set is a member of the set is called a group. Group theory is the study of the mathematical properties of such a collection of symmetry elements. Groups containing only symmetry elements that leave one point in the molecule unchanged are called point groups. In addition, crystals also have symmetries arising from translation through space and are called space groups. However, here we consider only point groups. Each distinct group of symmetry elements has a name.

We now present the Schoenflies naming system for point groups:

 

例子

 

 

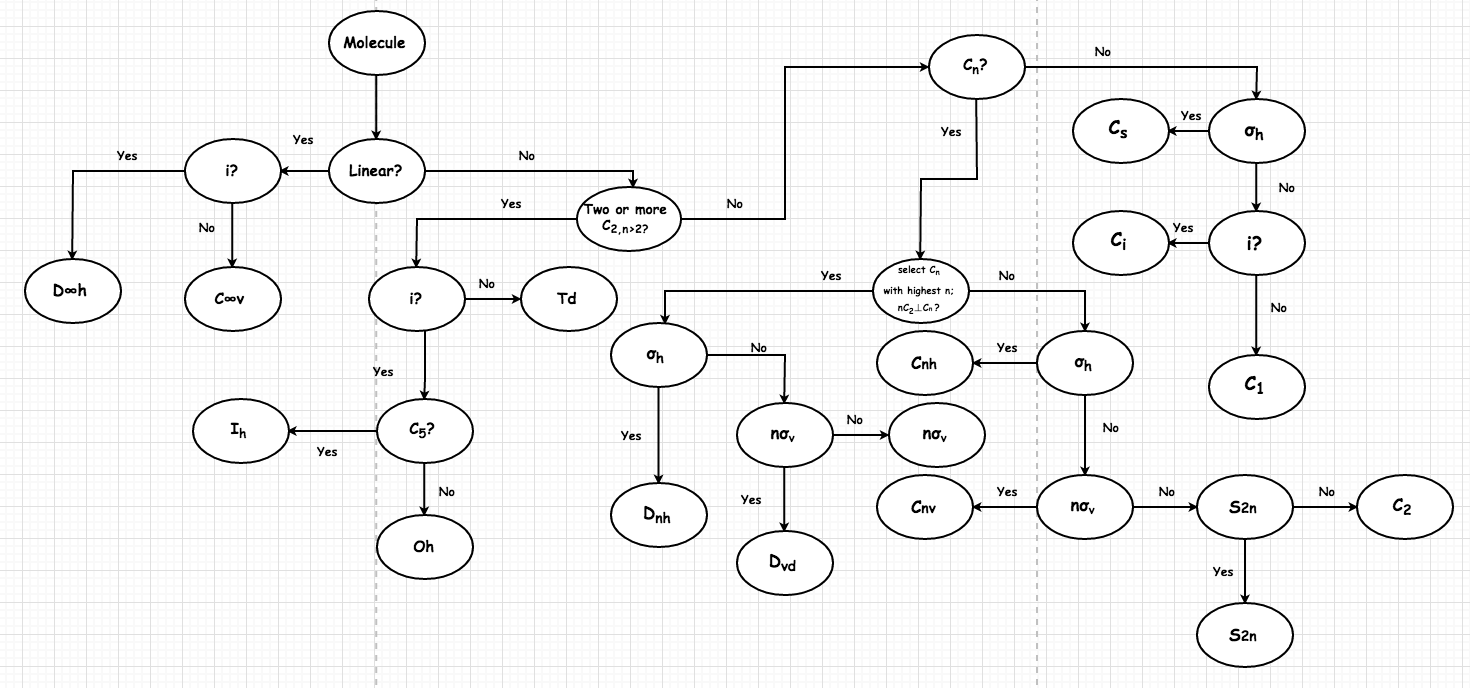
判断点群