BaTiO3极化强度计算
本文主要计算经典的铁电材料 BaTiO3 的极化强度。
BaTiO3 是钙钛矿结构,它的铁电相结构和中心对称结构如图所示,属于四方晶系。
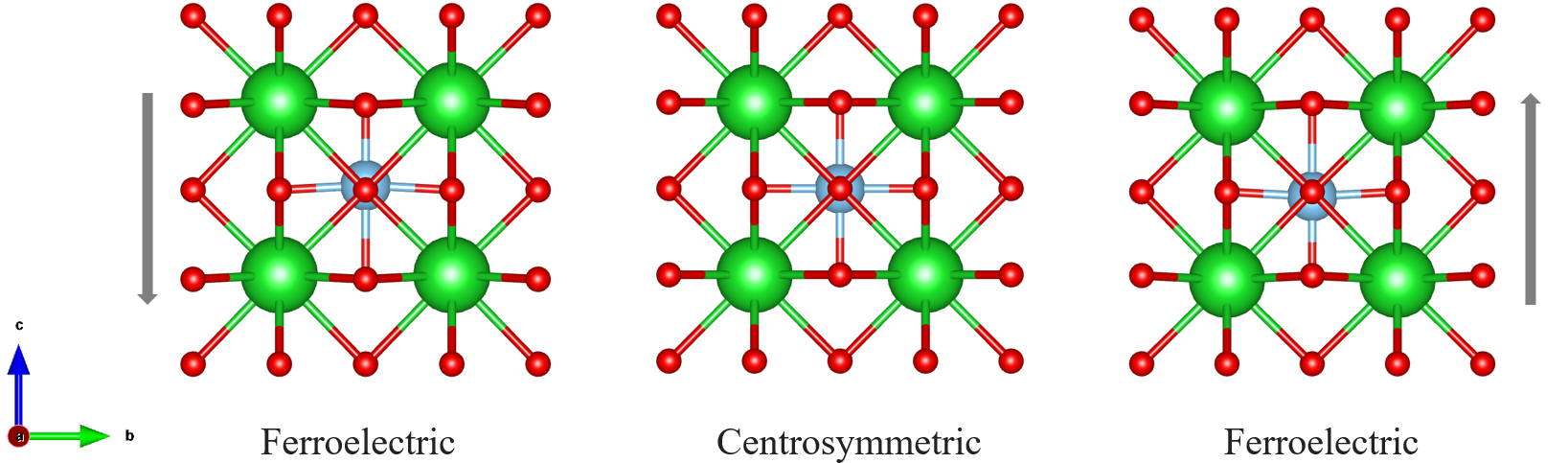
该铁电材料是沿着 c 方向极化,主要是 O 离子和 Ti 离子的移动的贡献。 例如,上图中的左边铁电相极化方向朝下,右边铁电相极化方向朝上。
极化强度详细计算步骤如下:
1) 先构造 BaTiO3 两种极化方向的晶格结构,并用 VASP 进行结构优化得到 CONTCAR;
2)将上一步优化后的两个结构分别放入创建好的 ini, fin 文件夹。利用 NEB 的 nebmake.pl 命令产生这两种极化方向的中间过渡结构 (vtst下载地址: Download — Transition State Tools for VASP (utexas.edu)),具体命令为:
nebmake.pl ini/CONTCAR fin/CONTCAR 32
这里的 '32' 是表示产生中间过渡的 32 种结构。执行上述命令后,当前文件夹下会产生 00, 01, 02, ..., 33 个文件夹,每个文件夹下有一个 POSCAR 文件。
3)对每个文件夹的结构进行一次 VASP 自洽运算,INCAR 文件里面需要额外设置 DIPOL 和 LCALPOL 参数。
DIPOL 参数可以选取任一坐标,但是保证同一体系采用相同值。
LCALPOL 参数是打开 极化运算。
详细INCAR见文章末尾。
为了批量化计算,我们可通过 shell 循环命令进行各个文件夹下的自洽运算,并且提取计算结果中的极化强度以及能量,具体脚本job.sh如下:
for i in 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
do
cp POTCAR INCAR KPOINTS $i
cd $i
mpirun vasp_std
grep 'dipole moment' OUTCAR|rev| awk '{printf ("%s ", $4)}'|rev|awk '{printf ("%f\n", $1+$2)}' >> ../dipole_c.dat
grep 'free energy TOTEN' OUTCAR | awk '{printf ("%s\n",$5)}' >> ../energy.dat
cd ..
done
注意,这里通过 grep 命令产生的 dipole_c.dat 文件记录的是沿着 c 方向的极化值,这是因为 BaTiO3 是沿着 c 方向极化的。对于具体的情况需要自行修改。
4) 处理和分析数据。
首先要理清数据单位。VASP 计算得到的 dipole moment 的单位是 e*Å,它与库仑之间换算为:
1e = 1.602176634 * 10^-19 C 1Å = 10^-10 m
三维体系的极化强度: 极化值除以体积。单位为 e/Å2;二维体系的极化强度:极化值除以面积。单位为 e/Å。
在这个例子中,BaTiO3 的体积为 64.3586 Å3。
ok,接下来,我们来处理数据。
① energy.dat 文件 (单位为 eV):
-39.58522034 -39.58715080 -39.58829399 -39.58877610 -39.58871626 -39.58822550 -39.58740707 -39.58635780 -39.58516726 -39.58391686 -39.58267911 -39.58151782 -39.58048834 -39.57963796 -39.57900393 -39.57861316 -39.57848117 -39.57861316 -39.57900393 -39.57963796 -39.58048834 -39.58151782 -39.58267911 -39.58391686 -39.58516726 -39.58635780 -39.58740707 -39.58822550 -39.58871626 -39.58877610 -39.58829399 -39.58715080 -39.58522034
这样,我们就得到每个中间结构 (image) 的总能:
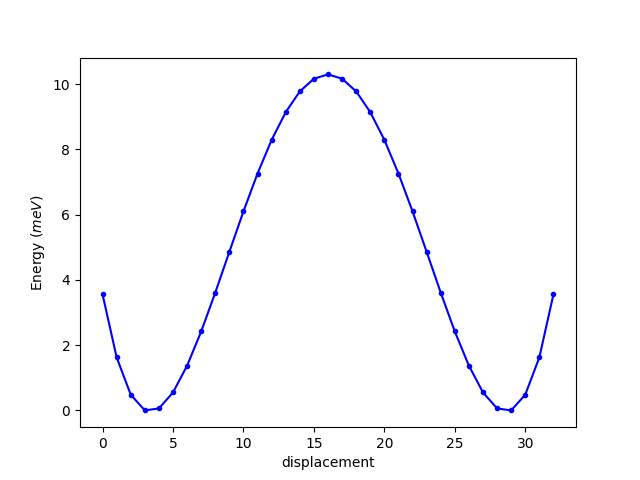
可发现,第4个image总能最低,即最稳定。
② dipole_c.dat 文件 (单位: e*Å):
-13.297040 -13.229310 -13.160540 -13.090720 -13.019860 -12.947930 -12.874960 -12.800990 -12.726030 -12.650150 -12.573400 -12.495880 -12.417670 -12.338900 -12.259680 -0.118270 0.000000 0.118270 12.259680 12.338900 12.417670 12.495880 12.573400 12.650150 12.726030 12.800990 12.874960 12.947930 13.019860 13.090720 13.160540 13.229310 13.297040
不同 image 的极化值如图所示:
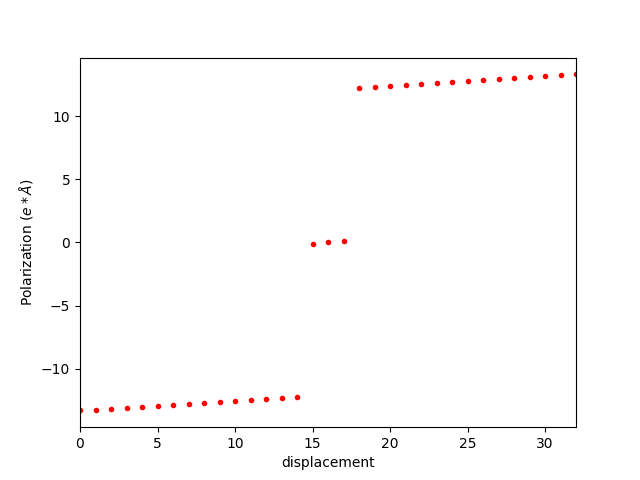
可以发现,该极化强度不是连续的,这是和选取的原胞有关,需要考虑极化量子的影响。BaTiO3 沿着 c 方向极化,所以需要对该极化值加减整数倍的 c 方向的晶格常数。这样我们得到下图:
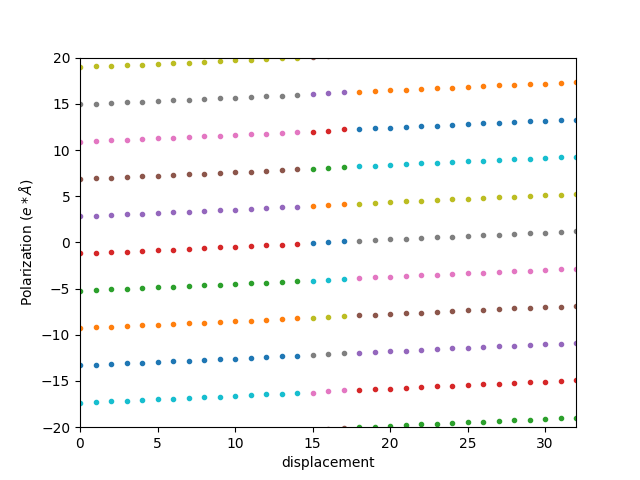
选取最靠近中间极化强度为 0 的那条曲线,即为 BaTiO3 的极化强度曲线:
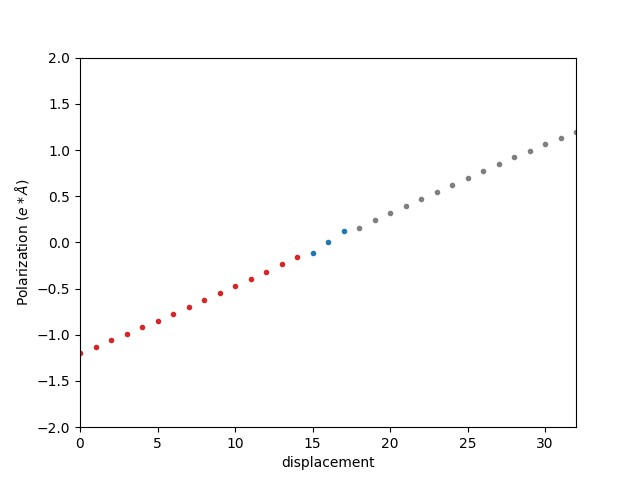
除以体积并进行简单的单位换算后为:
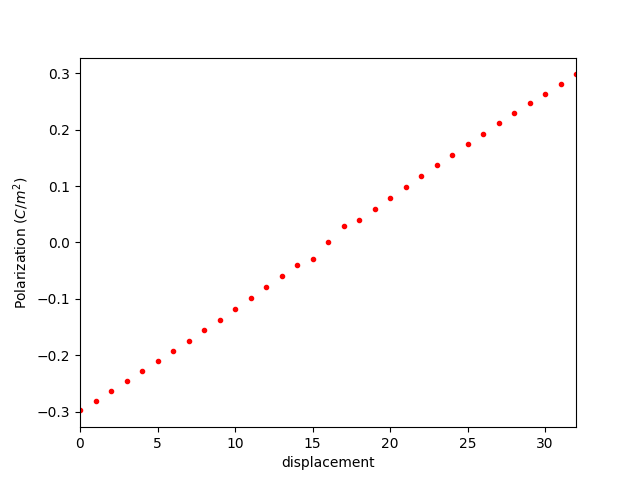
另外,我们也可以绘制极化值 P 与能量 E 曲线
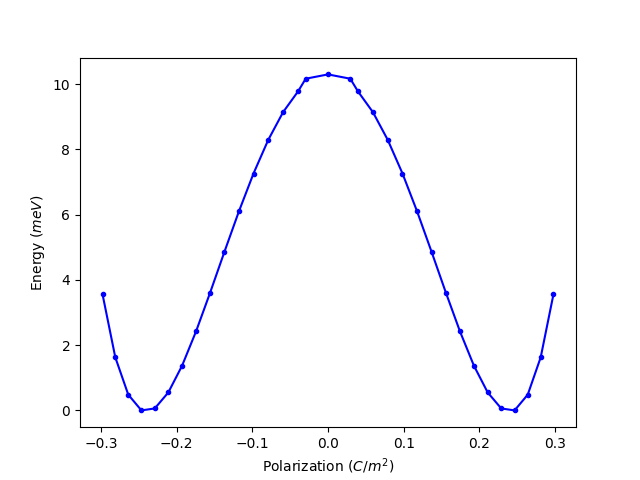
因此, BaTiO3 的极化强度大约为 0.248 C/m2,与文献中的实验结果 0.26 C/m2 吻合。(Physical Review, 99(4), 1161–1165, 1955 )
拟合 Landau-Ginzburg 公式
E= \sum_{i} A/2 * P_i^2 + B/4 * P_i^4 + C/6 * P_i^6 + D/2 * \sum_{i,j}(P_i-P_j)^2
拟合该多项式曲线,得到
E = 6062.434883706029*P^6 + 2437.756598493882*P^4 + -340.5806845162749*P^2 + 10.339600058315137
其中参数 A, B, C 分别为
A = -0.68116 eV *(m^2/C)^2 B = 9.75103 eV *(m^2/C)^4 C = 36.37461 eV *(m^2/C)^6
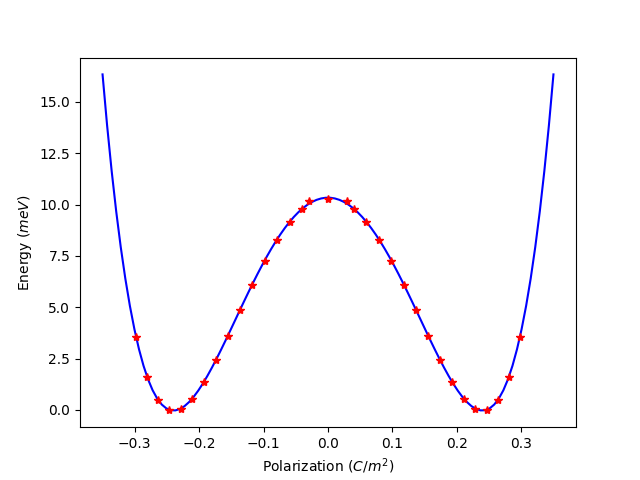
相关文件:
铁电相POSCAR
Ti Ba O 1.00000000000000 3.9944999999999999 0.0000000000000000 0.0000000000000000 0.0000000000000000 3.9944999999999999 -0.0000000000000000 0.0000000000000000 0.0000000000000000 4.0335000000000001 Ti Ba O 1 1 3 Direct 0.5000000000000000 0.5000000000000000 0.5142700000000000 0.0000000000000000 -0.0000000000000000 0.0000000000000000 0.5000000000000000 0.5000000000000000 0.9744770000000000 0.5000000000000000 0.0000000000000000 0.4876180000000000 0.0000000000000000 0.5000000000000000 0.4876180000000000
Ti Ba O 1.00000000000000 3.9944999999999999 0.0000000000000000 0.0000000000000000 0.0000000000000000 3.9944999999999999 -0.0000000000000000 0.0000000000000000 0.0000000000000000 4.0335000000000001 Ti Ba O 1 1 3 Direct 0.5000000000000000 0.5000000000000000 0.4857300000000000 0.0000000000000000 -0.0000000000000000 0.0000000000000000 0.5000000000000000 0.5000000000000000 0.0255230000000000 0.5000000000000000 0.0000000000000000 0.5123820000000000 0.0000000000000000 0.5000000000000000 0.5123820000000000
中心对称相POSCAR
Ti Ba O 1.00000000000000 3.9944999999999999 0.0000000000000000 0.0000000000000000 0.0000000000000000 3.9944999999999999 -0.0000000000000000 0.0000000000000000 0.0000000000000000 4.0335000000000001 Ti Ba O 1 1 3 Direct 0.5000000000000000 0.5000000000000000 0.5000000000000000 0.0000000000000000 0.0000000000000000 0.0000000000000000 0.5000000000000000 0.5000000000000000 0.0000000000000000 0.5000000000000000 0.0000000000000000 0.5000000000000000 0.0000000000000000 0.5000000000000000 0.5000000000000000
INCAR 文件:
SYSTEM=BaTiO3 ISTART =0 ICHARG =2 PREC =Accurate ENCUT =520 EDIFF =0.1E-07 ISMEAR = 0 LWAVE=.FALSE. LCHARG = .FALSE. NELM = 200 DIPOL = 0.5 0.5 0.5 LCALCPOL=.TRUE
绘制能量曲线的脚本
1 with open('energy.dat','r') as f: 2 content = f.readlines() 3 res = [float(i.strip('\n')) for i in content] 4 minres = min(res) 5 res = [1e3*(i-minres) for i in res] 6 import matplotlib.pyplot as plt 7 plt.figure() 8 plt.plot(res,'b.-') 9 plt.xlabel('displacement') 10 plt.ylabel('Energy ($meV$)') 11 plt.show()
绘制dipole曲线,以及考虑极化量子的脚本:
1 with open('dipole_c.dat','r') as f: 2 content = f.readlines() 3 res = [float(i.strip('\n')) for i in content] 4 5 import matplotlib.pyplot as plt 6 plt.figure() 7 plt.xlabel('displacement') 8 plt.ylabel('Polarization ($e*{\AA}$)') 9 plt.xlim([0,32]) 10 plt.plot(res,'r.') 11 12 13 ### 考虑极化量子 14 c = 4.0335000000000001 15 tmp = [] 16 N = 20 17 for j in range(N): 18 start = -N/2+j 19 tmp1 = [i+start*c for i in res] 20 # print(tmp1[0]) 21 tmp.append(tmp1) 22 plt.figure() 23 for i in tmp: 24 plt.plot(i,'.') 25 26 #plt.ylim([-2,2]) 27 plt.xlabel('displacement') 28 plt.ylabel('Polarization ($e*{\AA}$)') 29 plt.xlim([0,32]) 30 31 ### 单位换算 32 P = [-1.1965400000000006, -1.1288099999999996, -1.060039999999999, -0.990219999999999, -0.9193599999999993, -0.8474299999999992, -0.7744599999999995, -0.7004900000000003, -0.6255299999999995, -0.5496499999999997, -0.4728999999999992, -0.3953799999999994, -0.31716999999999906, -0.2384000000000004, -0.1591799999999992,-0.11827, 0.0, 0.11827, 0.1591799999999992, 0.2384000000000004, 0.31716999999999906, 0.3953799999999994, 0.4728999999999992, 0.5496499999999997, 0.6255299999999995, 0.7004900000000003, 0.7744599999999995, 0.8474299999999992, 0.9193599999999993, 0.990219999999999, 1.060039999999999, 1.1288099999999996, 1.1965400000000006] 33 plt.figure() 34 P = [i*0.248945227832799346 for i in P] 35 plt.xlabel('displacement') 36 plt.ylabel('Polarization ($C/m^2$)') 37 plt.xlim([0,32]) 38 plt.plot(P,'r.') 39 plt.show()
绘制极化值 P 与能量 E 曲线的脚本:
1 E = [0.0035557599999975764, 0.0016252999999935014, 0.0004821100000000911, 0.0, 5.983999999870093e-05, 0.0005505999999968481, 0.0013690299999993272, 0.0024182999999950994, 0.003608839999998281, 0.004859239999994713, 0.006096989999996083, 0.007258279999994954, 0.008287759999994648, 0.009138139999997463, 0.00977216999999797, 0.010162939999993625, 0.010294929999993485, 0.010162939999993625, 0.00977216999999797, 0.009138139999997463, 0.008287759999994648, 0.007258279999994954, 0.006096989999996083, 0.004859239999994713, 0.003608839999998281, 0.0024182999999950994, 0.0013690299999993272, 0.0005505999999968481, 5.983999999870093e-05, 0.0, 0.0004821100000000911, 0.0016252999999935014, 0.0035557599999975764] 2 P = [-1.1965400000000006, -1.1288099999999996, -1.060039999999999, -0.990219999999999, -0.9193599999999993, -0.8474299999999992, -0.7744599999999995, -0.7004900000000003, -0.6255299999999995, -0.5496499999999997, -0.4728999999999992, -0.3953799999999994, -0.31716999999999906, -0.2384000000000004, -0.1591799999999992,-0.11827, 0.0, 0.11827, 0.1591799999999992, 0.2384000000000004, 0.31716999999999906, 0.3953799999999994, 0.4728999999999992, 0.5496499999999997, 0.6255299999999995, 0.7004900000000003, 0.7744599999999995, 0.8474299999999992, 0.9193599999999993, 0.990219999999999, 1.060039999999999, 1.1288099999999996, 1.1965400000000006] 3 import matplotlib.pyplot as plt 4 import numpy as np 5 6 E = [1e3*i for i in E] 7 P = [i*0.248945227832799346 for i in P] 8 9 plt.figure() 10 plt.plot(P,E,'b.-') 11 plt.xlabel('Polarization ($C/m^2$)') 12 plt.ylabel('Energy ($meV$)') 13 14 f1 = np.polyfit(P, E, 6) 15 poly = '' 16 for i in range(len(f1)): 17 poly += '{}*x^{} + '.format(f1[i],len(f1)-i-1) 18 print(poly) 19 20 x = [ -0.35+0.7*i/99 for i in range(100)] 21 Eval = np.polyval(f1,x) 22 plt.figure() 23 plt.plot(x,Eval,'b') 24 plt.plot(P,E,'r*') 25 plt.xlabel('Polarization ($C/m^2$)') 26 plt.ylabel('Energy ($meV$)') 27 plt.show()
主要参考:
VASP计算铁电极化,以BaTiO3为例 - 哔哩哔哩 (bilibili.com)
Using Wannier Charge center to calculate Ferroelectric polarization (chengcheng-xiao.github.io)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号