九连环问题（递归）

题目描述

九连环是一种流传于山西省的传统民间的智力玩具，由九个圆环相连成串，以解开为胜。

九连环的九个环，一环扣一环地套在钗上。除了第 1 号环可以随时装上或卸下以外，其它环装上或卸下的条件是：在它的前面仅有紧靠它那一个环在钗上。即：当第 1 ~ i−2 号环都不在钗上，第 i−1 号环在钗上，这时可以装上或卸下第 i 号环。

输入格式

环数 操作(U表示装上, D表示卸下)

输出格式

装上或卸下九连环的操作步骤
每行显示一步操作，具体格式为：
环号: U或D (U表示装上，D表示卸下)

样例输入1

3 U

样例输出1

1: U
2: U
1: D
3: U
1: U

样例输入2

4 D

样例输出2

2: D
1: D
4: D
1: U
2: U
1: D
3: D
1: U
2: D
1: D

题意理解

这道题目我理解也是看了挺久
最总要的一句话就是：当第 1 ~ i−2 号环都不在钗上，第 i−1 号环在钗上，这时可以装上或卸下第 i 号环。

正解思路

我第一想法就是一个间接递归
我设置两个函数

f(i,1)函数代表，当前局面为[0,i]为空，装上单环i

f(i,0)函数代表，当前局面为[0,i-1]为空，i存在，卸下单环i，

digui(i,1),表示[0,i]为空，[0,i]全装上

digui(i,0),表示[0,i]全都存在，[0,i]全卸下来

思路我很详细的注释在代码里面了

#include<bits/stdc++.h>
using namespace std;
void f(int n,int k) {
	if(n==0)return ;
	if(n==1) {
		printf("%d: %c\n",n,k==1?'U':'D');
		return ;
	}
	f(n-1,1);//装上单环n-1 
	printf("%d: %c\n",n,k==1?'U':'D');//装上或卸下单环n 
	f(n-1,0);//卸下单环n-1 
}
void digui(int n,int k) {
	if(n==0)return ;
	if(n==1) {
		f(n,k);
		return ;
	}
	if(k) {
		f(n-1,1);//先装上单环n-1 
		printf("%d: %c\n",n,k==1?'U':'D');//装上单环n 
		digui(n-2,1);//装上全环n-2 
	}
	else {
		digui(n-2,0);//卸下全环n-2 
		printf("%d: %c\n",n,k==1?'U':'D');//卸下单环n 
		f(n-1,0);//卸下单环n-1 
	}
}
int main() {
	int n;char c;
	scanf("%d %c",&n,&c);
	digui(n,c=='U'?1:0);//装上或卸下，全部的环1-n 
}

做题时思路

给大家分享我自己打这题踩的坑，大家共勉

看题目第一反应
很显然的递归，模拟一遍之后我的第一想法，是间接递归
因为总结不出直接递归的写法，也没试过
我代码第一遍打完之后
整题10分拿了5分
因为PTA是不允许下载测试样例的
因为以前自己也出过题目，所以我知道数据应该是对半的
一半取的，一般卸的，抱着试一试的心态
我就在代码里面加了一句，如果是'U'操作，那么直接结束程序

果然还是拿了5分，这时候我就知道是我程序'U'操作有问题，'D'操作是没问题的

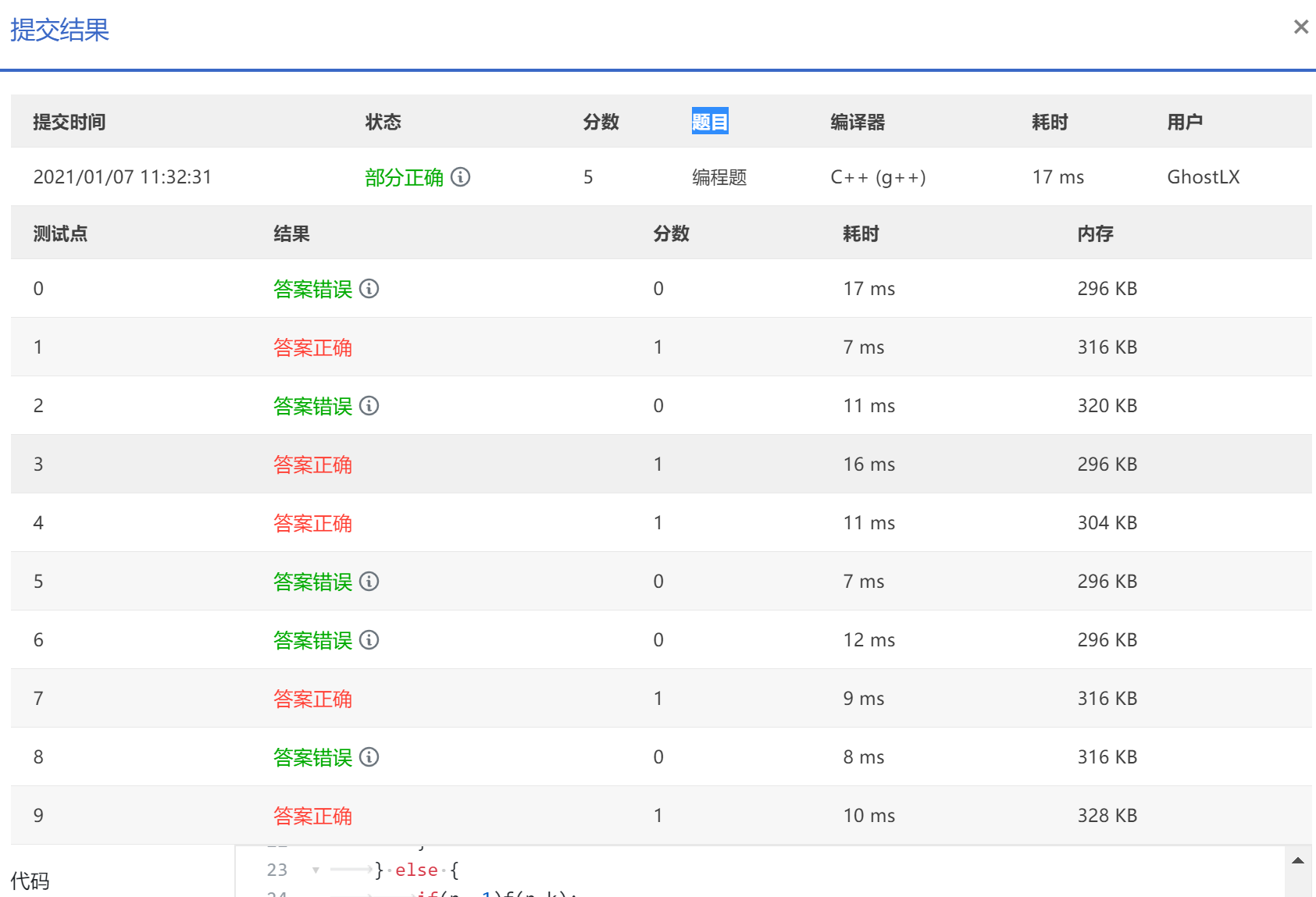
然后我改了接近一个小时的bug，实在找不出来我U操作代码的思路哪里有问题
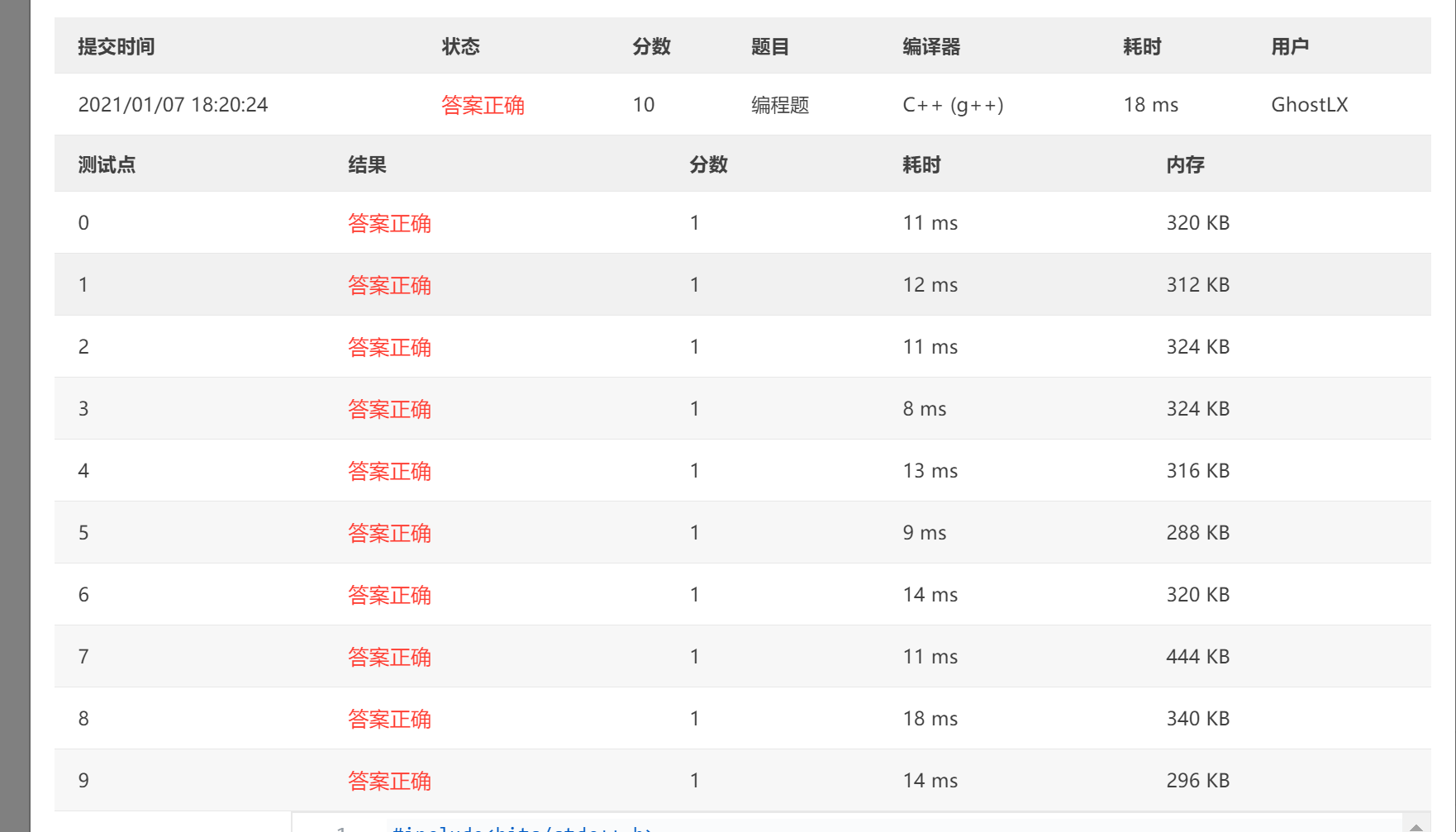
于是我就一个大佬一起帮忙打这题，他打完之后交上去ac了，
他找我代码的思路，觉得没有任何问题
我俩程序对拍，结果发现输出一模一样
我俩找debug快一个半小时
然后我们就开始质疑，发现我程序真的没问题，就开始质疑编译器了
我们一直把重点放在递归函数上面，发现main函数，我char c定义成int c

int main() {
	int n,c;
	scanf("%d %c",&n,&c);
	int k=c=='U'?1:0;
	if(k)digui(n,1);
	else digui(n,0);
}

我把int改成char之后，就ac了……

我就去查一下PTA的编译器是6.5.0的

我的编译器是8.1.0

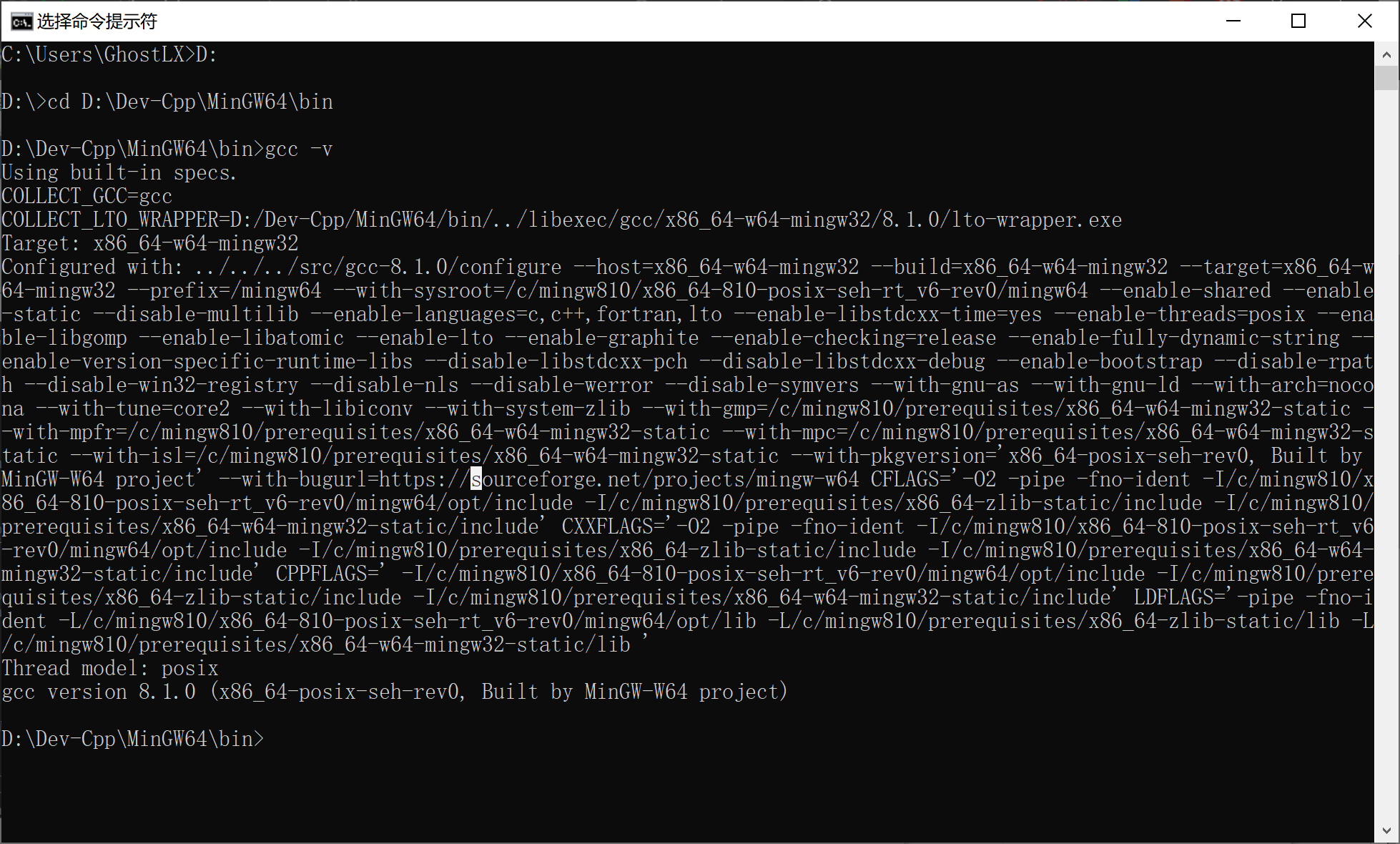
有时候犯这种弱智错误的情况，可能你的编译器太聪明了
以至于你改不出来
所以出现bug的情况，就可以用到pta网站自带的自测
就可以一定意义上面避免编译器版本不同而带来订正N久的问题