SG函数和尼姆博弈

尼姆博弈

模型：有n堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取1个，多者不限，最后取光者得胜。
下文中我们把物品假设为是石子

性质及证明

规定\(sum=a_1\bigoplus a_2\bigoplus ……\bigoplus a_i\bigoplus……\bigoplus a_n\)
其中\(a_i\)表示第i堆物品有多少石子，总共n堆
\(\bigoplus\)代表xor即'^',表示异或操作
性质1：当\(sum= 0\)时，先手必败，记为P点，即必败点
性质2：当\(sum\neq 0\)时，先手必胜，记为N点，即必胜点
性质3：\(\exists i\)，满足\(sum\bigoplus a_i\leq a_i\)

性质一和性质二

我们易得，初始状态\({a_1,……,a_n}\)，经过两人之手，总会得到末状态{0,0,……，0}
任意得到当一人面对末状态的时候，他没办法取任何石子，那么他就输了，即这是一个P点
在前面的威佐夫博奕中我已经证明过P点后面对应的必然是N点，N点后对应的必然是P点
这边穿插一下SG定理

SG定理

给定一个有向无环图和一个起始顶点上的一枚棋子，两名选手交替的将这枚棋子沿有向边进行移动，无法移动者判负。事实上，这个游戏可以认为是所有Impartial Combinatorial Games的抽象模型。也就是说，任何一个ICG都可以通过把每个局面看成一个顶点，对每个局面和它的子局面连一条有向边来抽象成这个“有向图游戏”。

下面我们就在有向无环图的顶点上定义Sprague-Garundy函数。
首先定义mex(minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。
对于一个给定的有向无环图，定义关于图的每个顶点的Sprague-Garundy函数g如下：sg(x)=mex{ sg(X') | X'是x的后继 }。
来看一下SG函数的性质。首先，所有的terminal position所对应的顶点，也就是没有出边的顶点，其SG值为0，因为它的后继集合是空集。


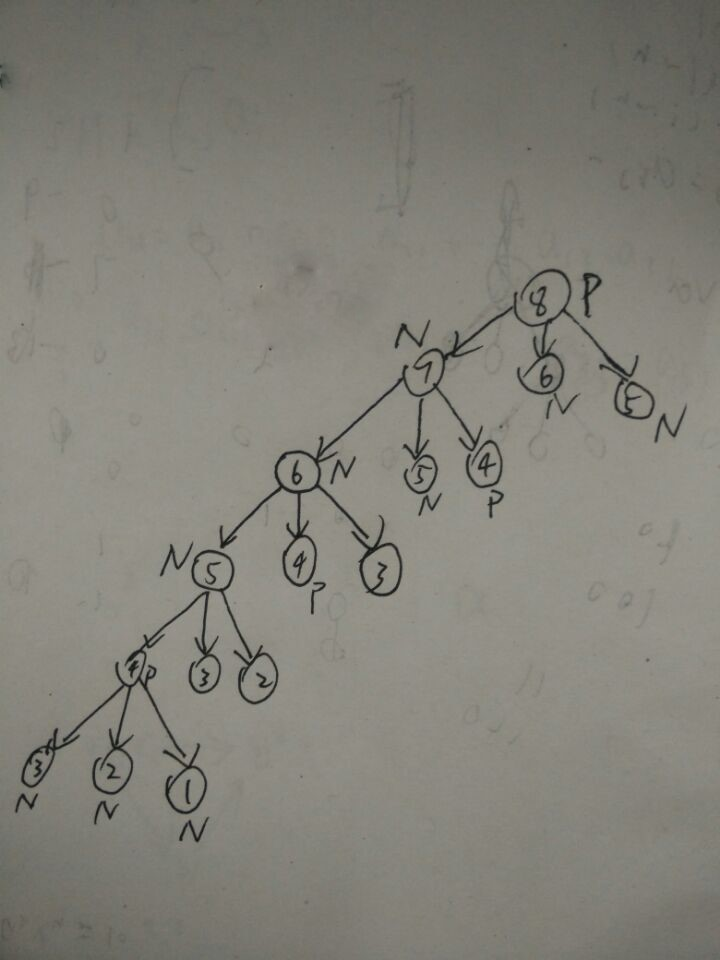
易得以下两个性质
性质一:SG(X)==0时，它的任意后继节点SG(X') \(\neq\) 0
性质二:SG(X)!=0时，它的后继节点必然存在一个SG(X')=0
公平组合游戏类的题目，都有一个前提条件，就是双方足够聪明
如果我有两种选择，一种是让你面对N点，一种是让你面对P点
显然，为了赢，我必然会让你面对P点，于是我们可以想象一棵树，
它的最底层是P点，然后往上N,P点按层交错分布

因为最底端是SG(x)=0的点，那么显然如果把末状态所在层设为0，往上递增编号
那么所有的奇数层都是N点，偶数层都是P点
结合SG函数的两个性质，SG(X)=0点对应偶数层，SG $\neq$0的点对于奇数层
也就可以通过判断SG(x)是否为0来判断先手是否必胜了

sum和SG函数的关系

那么我们再看回来，异或和sum和SG函数有什么关系呢
设sum'为x的后继状态X'对应的异或和
\(sum'=a_1\bigoplus a_2\bigoplus ……\bigoplus a_i'\bigoplus……\bigoplus a_n\)
这边穿插一个异或的性质

异或也被称为不进位的加法，即统计二进制第i位上1的个数，
n个数的异或和在第i位上1的个数为奇数时结果为1，为偶数结果为0

因为我们是取石子，即必然\(a_i'<a_i\)，改变了一个数，那二进制中某些位的1个数必然发生改变
则sum'发生变化
所以对于sum=0，必然有sum'\(\neq\) 0，与SG性质一相同
那么对于sum\(\neq\) 0是否存在一种sum'=0呢？答案是肯定的
因为是公平组合游戏，我不可能给我的对手最有利的局势
我们只可能给他若干种后继状态中最坏的那种，也就是sum=0
接下来要证明的就是sum!=0的后继状态中，必然存在sum'=0
对于某个局面(a1,a2,...,an)，若a1^a2...^{an!=0，一定存在某个合法的移动，将ai改变成ai'后满足a1}a2^...ai'^...an=0。
不妨设a1^a2...^an=k，则一定存在某个ai，它的二进制表示在k的最高位上是1（否则k的最高位那个1是怎么得到的）。
这时ai^{k<ai一定成立。则我们可以将ai改变成ai'=ai}k，此时a1^a2...^ai'...^an=a1a2^...an^k=0。(异或满足交换律)
证毕
即两边=0和\(\neq\) 0的情况对于的后继都是一样的
这样我们就可以把sg那棵树的性质转移到nim这边来
(半理性半感性证明)
所以nim博弈的性质一性质二成立

性质三

\(\exists i\)，满足\(sum\bigoplus a_i\leq a_i\)

设除了第i堆外，其余堆的异或和为H，则H=sum^ai(因为异或满足消除律)
显然H^ai=sum\(\neq\) 0 ，
上面性质一二的证明过程，我们再拿过来继续用
对于某个局面(a1,a2,...,an)，若a1^a2...^{an!=0，一定存在某个合法的移动，将ai改变成ai'后满足a1}a2^...ai'^...an=0。
不妨设a1^a2...^an=k，则一定存在某个ai，它的二进制表示在k的最高位上是1（否则k的最高位那个1是怎么得到的）。
这时ai^{k<ai一定成立。则我们可以将ai改变成ai'=ai}k，此时a1^a2...^ai'...^an=a1a2^...an^k=0。(异或满足交换律)

继续证明

H=sum^ai,因为sum的最高位j是1，ai的最高位j也是1
sum统计了奇数个1，则H中统计偶数个1，所以H的第j位是0，所以H<ai
证毕

代码的话，回头再完善吧

本文参照：https://blog.csdn.net/strangedbly/article/details/51137432