【主席数】可持续化线段树
本文参考:https://blog.csdn.net/ModestCoder_/article/details/90107874
预备知识
线段树,权值线段树,前缀和思想,等等
引入
约定:下文中的第\(k\)小/大,写作\(kth\)
给定一段区间,静态求区间\(kth\)
思想的推进
思考优化策略
给定n个数,可以对于每个点i都建一棵权值线段树,维护1~i这些数,统计每个不同的数出现的个数(权值线段树以值域作为区间)
这样,n棵线段树就建出来了,第i棵线段树代表1~i这个区间
例如,一列数,n为6,数分别为1 3 2 3 6 1
首先,每棵树都是这样的:
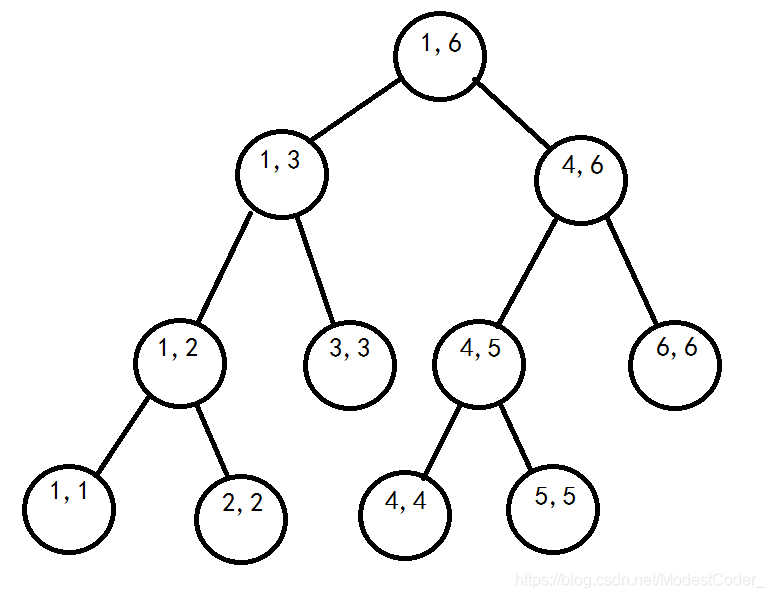
以第4颗线段树为例,1~4四个数分别为1 3 2 3
主席树的本质,就是权值线段树
节点类似于,桶排序中的桶
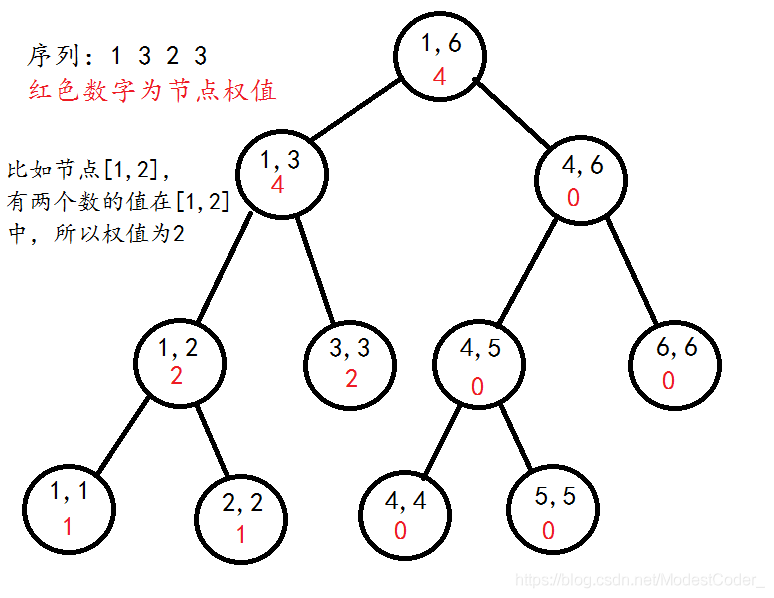
因为是同一个问题,n棵权值线段树的形状是一模一样的,只有节点的权值不一样
所以这样的两棵线段树之间是可以相加减的(两颗线段树相减就是每个节点对应相减)
想想,第x棵线段树减去第y棵线段树会发生什么?
第x棵线段树代表的区间是[1,x]
第y棵线段树代表的区间是[1,y]
两棵线段树一减
设\(x>y,[1,x]-[1,y]=[y+1,x]\)
所以两个区间相减,可以得到一个新的区间的线段树
这样一来,任意一个区间的线段树,都可以由我这n个基础区间表示出来了
这就是非常经典的前缀和思想
这样任意一个区间,都有一个对应的线段树
我们只需要在该区间,找\(kth\)的值就行
这就是主席树的一个核心思想:前缀和思想
现在还有一个严峻的问题,就是n棵线段树空间太大了!
如何优化空间复杂度,是主席树另一个核心思想
我们发现这n棵线段树中,有很多重复的点,这些重复的点浪费了大部分的空间,所以考虑如何去掉这些冗余点
假设现在有一棵线段树,序列往右移一个单位,建一棵新的线段树
对于一个儿子节点的值域区间,如果权值有变化,那么新建一个节点,否则,连到原来的那个节点上
这样说可能有点抽象
现在来看几个例子
序列4 3 2 3 6 1
区间[1,1]的线段树(蓝色节点为新节点)
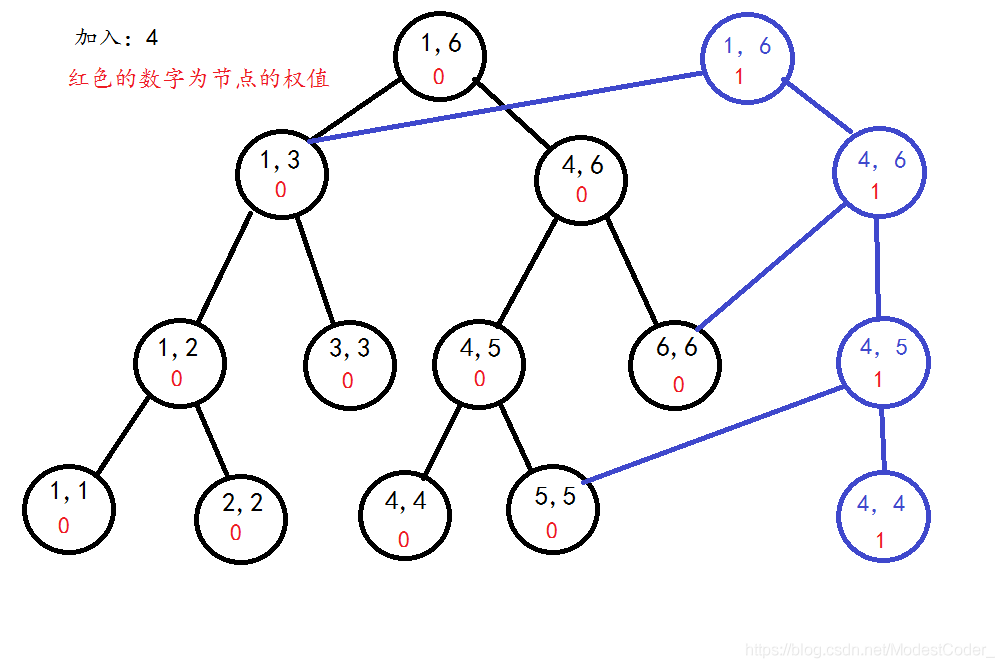
区间[1,2]的线段树(橙色节点为新节点)
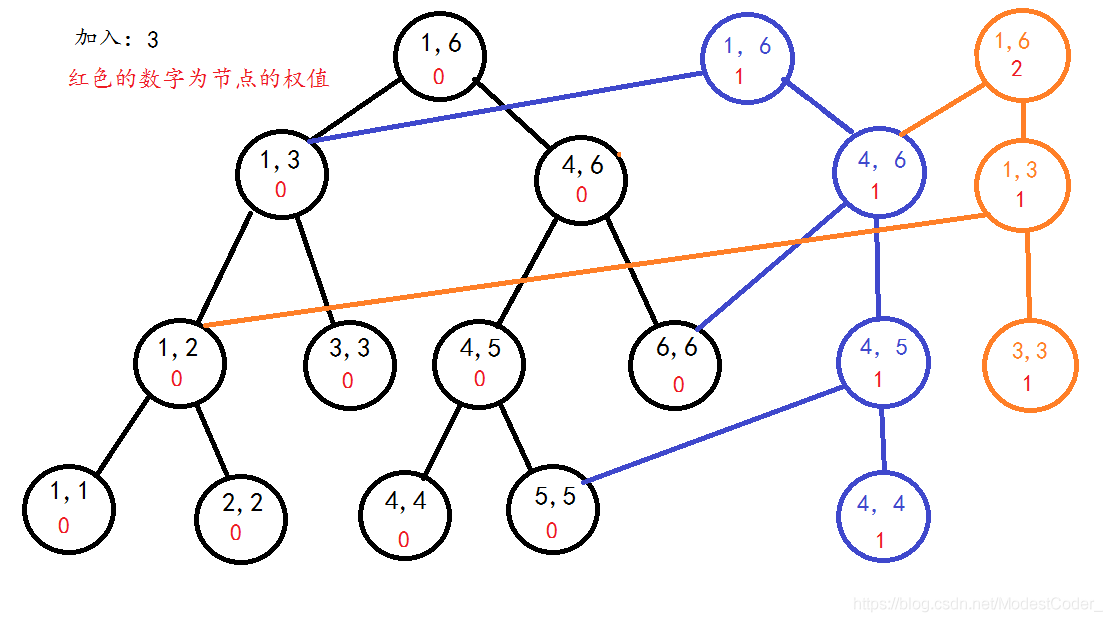
区间[1,3]的线段树(紫色节点为新节点)
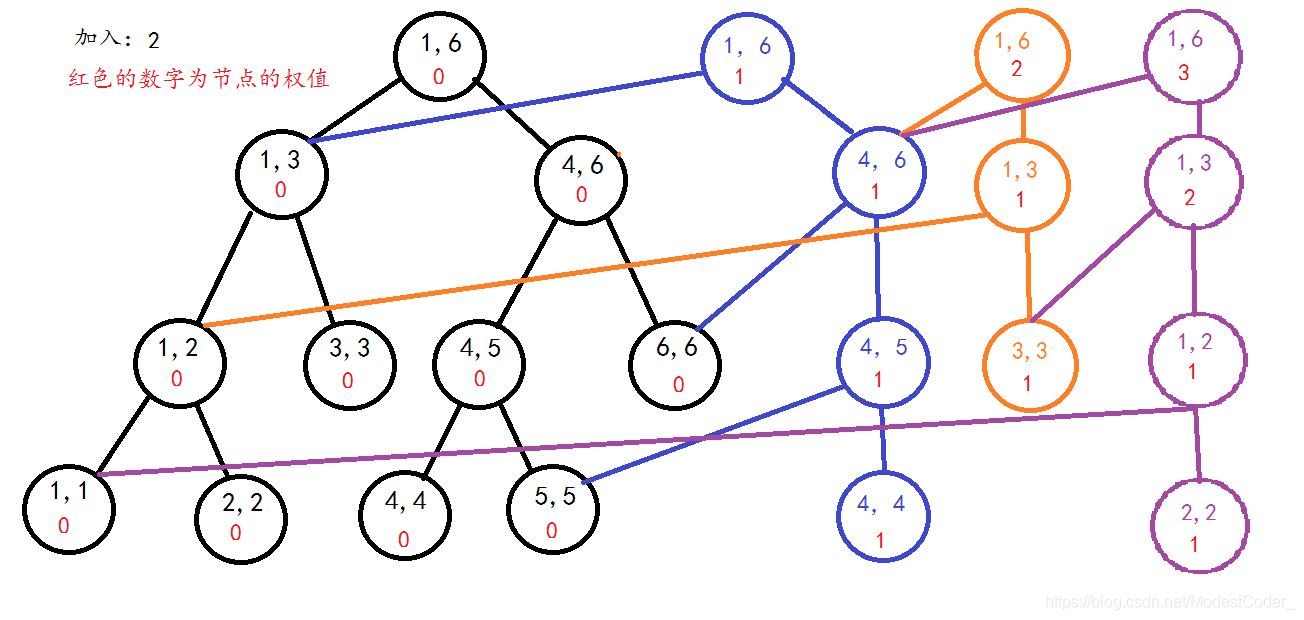
当然,读到这里你会被主席树的思想给秀到,毕竟太优秀了
主席树的思想就讲到这边,接下来讲讲代码
变量含义
a、b数组,一般储存输入数据
sz:节点个数
rt数组:存储每棵线段树的根节点编号
lc、rc数组:记录左儿子、右儿子编号,类似于动态开点
sum数组:记录节点权值
q:记录离散化后序列长度,也是线段树的区间最大长度
权值线段树的为什么都需要离散化?因为权值线段树的每个节点是一个桶,叶子节点统计一个数值在区间出现的次数,如果没有离散化,会多建很多不必要的节点,浪费大量的空间。
主席树的本质也是权值线段树,所以主席树也需要离散化
主席树
主席树又名可持久化线段树,顾名思义,它可以把问题的历史信息全部记录下来,实现可持久化
首先,数可能会很大,然而n却只有200000,所以要离散化,用到unique函数
for (int i = 1; i <= n; ++i) a[i] = read(), b[i] = a[i];//复制a数组
sort(b + 1, b + 1 + n);
q = unique(b + 1, b + 1 + n) - b - 1;//unique函数,返回值为去重后的序列长度
建一棵空树,虽然我也不知道为什么,但是大家都这么干,虽说不建也没关系,以防万一?反正建一下也不会错
build(rt[0], 1, q);//空树看成第0棵树
1~n依次建树
p代表a[i]在离散化去重后b中对应的下标
for (int i = 1; i <= n; ++i) {
p = lower_bound(b + 1, b + 1 + q, a[i]) - b;//找出新加入的点的位置,用lower_bound
rt[i] = update(rt[i - 1], 1, q);
}
查询操作
while (m--) {
int l = read(), r = read(), k = read();
printf("%d\n", b[query(rt[l - 1], rt[r], 1, q, k)]);//前缀和思想,[1,r]-[1,l-1]=[l,r]
}
build函数
void build(int& rt, int l, int r) {
rt = ++sz, sum[rt] = 0;//新点
if (l == r) return;//叶子结点,退出
int mid = (l + r) >> 1;//mid
build(lc[rt], l, mid);
build(rc[rt], mid + 1, r);//往下走
}
update函数
int update(int o, int l, int r) {
int oo = ++sz;//新点
lc[oo] = lc[o], rc[oo] = rc[o], sum[oo] = sum[o] + 1;//继承原点的信息,权值+1
if (l == r) return oo;//叶子结点,退出
int mid = (l + r) >> 1;//mid
if (p<=mid) lc[oo] = update(lc[oo], l, mid);
else rc[oo] = update(rc[oo], mid + 1, r);//新加入的节点在哪个区间,就走到哪个区间里去
return oo;//返回值为新点编号
}
int query(int u, int v, int l, int r, int k) {//u、v为两棵线段树当前节点编号,相减就是询问区间
int mid = (l + r) >> 1, x = sum[lc[v]] - sum[lc[u]];//sum相减,前缀和思想
if (l == r) return l;//叶子结点,找到kth目标,退出
if (x >= k) return query(lc[u], lc[v], l, mid, k);
else return query(rc[u], rc[v], mid + 1, r, k - x);
//kth操作,排名<=左儿子的数的个数,说明在左儿子,进入左儿子;
//反之,目标在右儿子,排名需要减去左儿子的权值
}
注意:线段树一般开4倍n的空间,而主席树开32倍的空间
代码实现
#include <bits/stdc++.h>
#define maxn 200010
using namespace std;
int a[maxn], b[maxn], n, m, q, p, sz;
int lc[maxn << 5], rc[maxn << 5], sum[maxn << 5], rt[maxn << 5];
//空间要注意
inline int read() {
int s = 0, w = 1;
char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') w = -1;
for (; isdigit(c); c = getchar()) s = (s << 1) + (s << 3) + (c ^ 48);
return s * w;
}
void build(int& rt, int l, int r) {
rt = ++sz, sum[rt] = 0;
if (l == r) return;
int mid = (l + r) >> 1;
build(lc[rt], l, mid); build(rc[rt], mid + 1, r);
}
int update(int o, int l, int r) {
int oo = ++sz;
lc[oo] = lc[o], rc[oo] = rc[o], sum[oo] = sum[o] + 1;
if (l == r) return oo;
int mid = (l + r) >> 1;
if (mid >= p) lc[oo] = update(lc[oo], l, mid); else rc[oo] = update(rc[oo], mid + 1, r);
return oo;
}
int query(int u, int v, int l, int r, int k) {
int mid = (l + r) >> 1, x = sum[lc[v]] - sum[lc[u]];
if (l == r) return l;
if (x >= k) return query(lc[u], lc[v], l, mid, k); else return query(rc[u], rc[v], mid + 1, r, k - x);
}
int main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) a[i] = read(), b[i] = a[i];
sort(b + 1, b + 1 + n);
q = unique(b + 1, b + 1 + n) - b - 1;
build(rt[0], 1, q);
for (int i = 1; i <= n; ++i) {
p = lower_bound(b + 1, b + 1 + q, a[i]) - b;
rt[i] = update(rt[i - 1], 1, q);
}
while (m--) {
int l = read(), r = read(), k = read();
printf("%d\n", b[query(rt[l - 1], rt[r], 1, q, k)]);
}
return 0;
}
复杂度分析
时间复杂度
建树 \(O(nlogn)\)
每次添加一颗新的线段树,就需要建立\(\log_{2}{n}\)个节点,总共需要加入n棵
询问 \(O(mlogn)\)
总复杂度\(O((n+m)logn)\)
空间复杂度
一般为\(O(nlog^2 n)\)
后记
发明主席树的人叫黄嘉泰,缩写是HJT,所以叫做主席树



 浙公网安备 33010602011771号
浙公网安备 33010602011771号