BUPT训练随笔(round 4）

BUPT T4

目前已掌握：ABCDEFGHK
A：要你求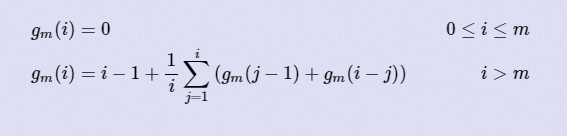

思路：队友做的0.0，大概的想法是有的，但是赛中没继续往下想队友就切了。首先求和符号里面的两个东西本质上是一个东西这样变成g[i]=i-1+2/i*sum(g[j-1])，然后要想着脱掉求和符号，就对式子两边先同乘i再进行差分ig[i]-(i-1)g[i-1]=2(i-1)+2*g[i-1],即g[n]/(n+1)-g[n-1]/(n)=（2n-2）/n(n+1)，发现只需要对右边这个东西求个前缀和就好了。右边=(1/n-1/(n+1))*(2n-2)=2*sum(1/i)-(2n-2)/(n+1)，只要求sum(1/i)即可。发现数据范围实在比较大（n=1e9），发现可以使用分块打表处理，就可以通过本题了。m的限制其实并没有什么用，只要稍微修改一下式子即可

B：网格图中给定多条延x/y轴方向出射的射线，求整个图被分割成几个联通块。保证不会有两条射线重合。

思路：考虑y轴方向对x轴方向的射线的贡献。那么发现是二维数点问题。可以用扫描线+线段树水过去。

C：给定n<=40个数，要你计算所有可能的子集合中数位中“4”的个数

思路：n<=40，首先排除DP和三方做法。想到状压或者爆搜。发现可以考虑折半搜索，然后我们发现数位“4”这个东西很不好处理，所以必然要对每个数位分开单独讨论。发现可以预处理A,B两个集合内子集合的状态（不超过2^20）然后一一配对考虑对答案的贡献。又发现对于每一个A集合中的数，B集合中有贡献的一定是一段区间，而且区间左右端点随着A中数的增大单调递减，可以用双指针扫描。但是发现复杂度为2^nlog2^n*10，不能通过。考虑优化排序的复杂度，发现基数排序可以完美解决这个问题，所以就能通过了。

D：要你找出排列1~n的一个子序列，满足ai^2=ai-1*ai+1,求方案数

思路：赛中一直想着如何对单独质因子讨论然后合并质因子的答案，结果发现并不是很有用。赛后通过题解才明白可以枚举公比。首先长度为1,2的可以单独计算，长度>4的可以发现末项必须整除q^(len-1)，所以可以暴力枚举，难度在于长度=3的。由于数学太菜这里只能放出来题解中的式子（其实不会用latex）然后发现后者是个数论分块，前者可以杜教筛。（我这就去补数学呜呜呜）（未实现，待填坑）

 

E：给你一个字符串，A要让字符串字典序尽量小，B要让字符串字典序尽量大。每次可以把一个字符i->(i+1)%26，A先操作，求最终字符串的样子。

思路：队友做的0.0，赛后感觉思路还是很有趣的。如果当前有个z，那么A会让它变成a,B会让它变成b，游戏结束。如果当前有个y，那这时候A不能动，B也不能动。如果是其他字母A会直接选择结束游戏。

F：有4种硬币 10 20 50 100，求组合出所给出的多种数字最少使用的硬币数量

思路：队友做的0.0，首先发现答案很大的时候肯定100用的越多越好，我们又发现10最多用1个，不然多余的10可以用20代替，20最多用4个，50最多用1个。这样我们可以枚举10 20 50的用量，然后暴力背包计算即可。

G：给定一棵树，统计(L(a,b),L(c,d))的有序二元组的个数，L(a,b)表示a到b路径上的点数。需要保证a->b,c->d互不相交。

思路：赛中做的。我们发现如果(x,y)有的话，(x,y-1),(x-1,y)必然也会有。那么我们只需要找到(x,maxxi)统计答案即可，问题转化成取两条尽量长的链。很自然就会想到树的直径，显然这会产生(Lmax,?)和(?,Lmax)，?可以通过树型DP求出最大值，但是这只是一种拆分，有可能两条链都含有树直径的一部分，所以我们要枚举断点，分别对两边的两个联通块求直径。也可以通过树形DP实现。

H：给定n个ai,n个bi，让ai,bi一一配对之后，计算sum aixorbi 而且要保证答案中不存在j,k(aixorbj>aixorbi&&akxorbi>aixorbi)

思路：一看到这个就想到trie树贪心了。只是赛中考虑方案是否合法想了很久。（题目看错了，&&看成了||）发现如果直接trie树每次找最大xor值是可以满足这个方案的。所以写完就A了。

K：题意过于难以描述，贴图为敬。

 

思路：完全没有思路.jpg 队友做的 队友tql 赛后仔细理解了一下题解。直接看构造其实会比较懵逼，因为并没有道理。但是我觉得AG佬的赛后评讲比较有道理。首先其实都会往分治的方向去靠，考虑合并区间的答案，然后根据计数过程中遇到的不能直接利用数学公式的东西设计一个新的DP方程来计算。本篇题解中h->g->f的推导思路应该来说是比赛中能想到这种题目做法的唯一方法。