【笔记】辐射场
Radiance Fields
The Radiance Field – Nathan Reed’s coding blog (reedbeta.com)
CMU 15462 Slide
Neural Radiance Fields (NeRF)
前置知识
目的
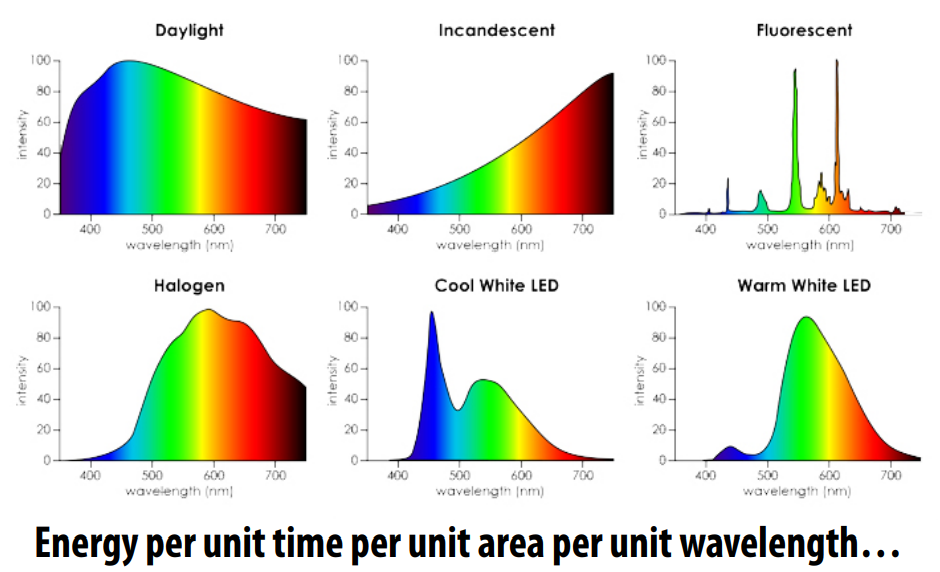
量化光的测量
如何量化光强
对于一些光子:
- Radiant energy: 碰撞总数
- Radiant flux: 每秒碰撞数
- Irradiance: 每秒每单位面积碰撞数
不同的光子碰撞,贡献不同,如何量化?
- Radiant energy:
h和c是常数,只有要关注,它也代表了颜色
-
Radiant flux:
-
Irradiance:
The average flux
如何量化颜色
描述irradiance per unit wavelength
单位时间单位面积单位波长的能量
Lambert's Law
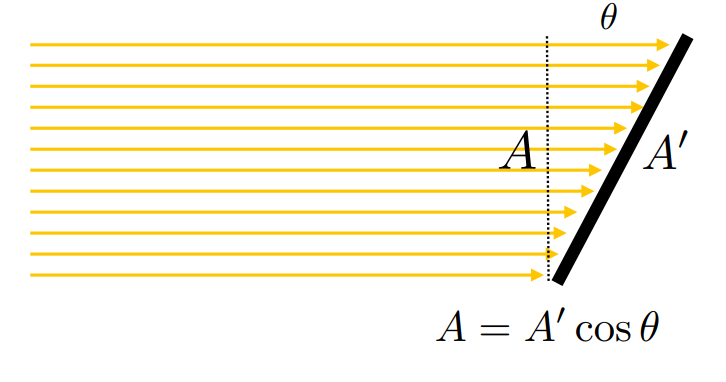
斜着照,用正交投影面积
简单光照
单位光线向量和平面单位法向量内积,即为光强

(通常)把光源放到无穷远,得到平行光
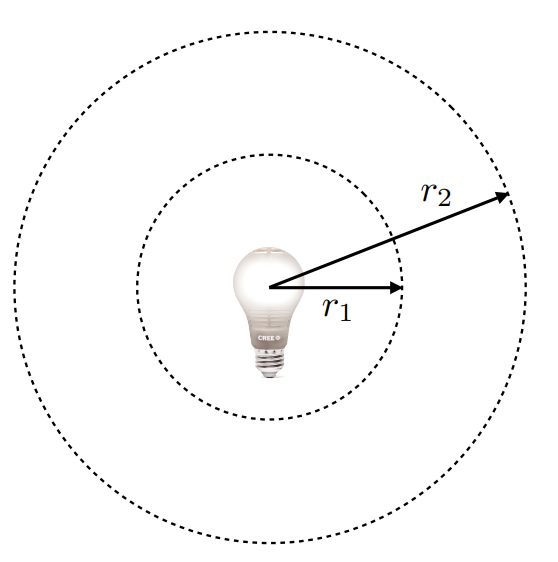
对于点光源,其irradiance与平方成反比(类似高斯定理?)
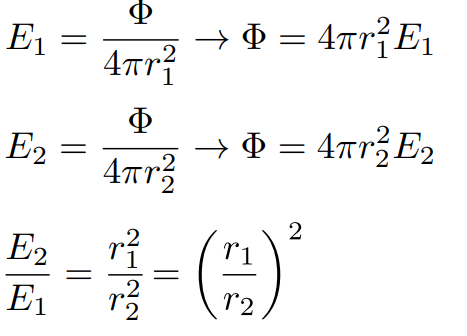
立体弧度
一个圆有个弧度
弧度
一个球有个弧度
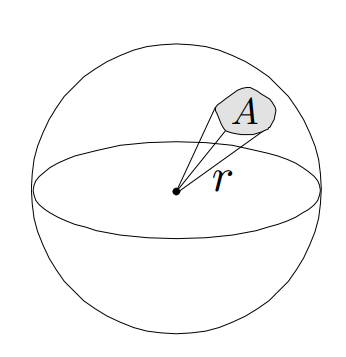
立体弧度
Radiance是irradiance的立体弧度密度
定义
辐射场是一个五维函数
左边的是三维空间,是球坐标下的视角
右边的是线性RGB空间
所以,辐射场是这样的一个五维函数:
亦可以写成向量形式
是位置向量,是视角的单位向量
也就是说,Radiance是一条沿着方向的光线通过点的能量
*渲染方程
一点的辐射由两部分组成,一部分是自己发出的(emit),另一部分是该点折射在方向上的辐射
其中为入射方向的半球集,为散射函数,为方向的辐射,为和的夹角
本文来自博客园,作者:GhostCai,转载请注明原文链接:https://www.cnblogs.com/ghostcai/p/15705519.html




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· winform 绘制太阳,地球,月球 运作规律
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具
· AI 智能体引爆开源社区「GitHub 热点速览」