做题记录1

洛谷6028

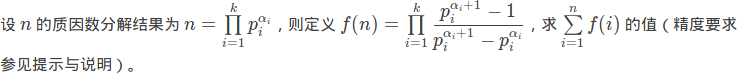
题解


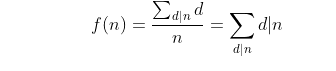
把约数提到最前面，这样就可以整除分块了，然后再套用神奇的求和
记住这个公式， 记住欧拉常数的值

快速乘

10.3 T1煎蛋的诱惑

想象左括号为向右上走一步，右括号为向下走一步，基准线为y=a，则这条线的意义为有-a个右括号是没有匹配上的，在x轴上则说明没有右括号是失配的。
一共有n个左括号n个右括号所以会走到（2n,0) 有m个右括号适配，也就是说最低点恰好碰到y=-m这条线，沿这条线翻折会到（2n,-2m)这是总的方案数
2n选出来n+m向下走。
不合法的方案数是碰到y=-m-1的，将其翻折会到(2n,-2m-2)这是不合法的方案,从2*n步选出(n+m+1)步向下走。

T2数据结构

可以根据二项式定理，得出\((x+1)^k - x^k = \sum_{i=0}^{k-1} C_{k}^{i} x^{i}\) 可以维护这些数的0到k次方的和，复杂度为O（mkk）
还有一种方法是记录累积加1的次数，若插入一个数为x，此前已经累计加1加了y次，那么相当于插入了x-y进去，每个数如此，这样答案为\(\sum (xi+y)^{k}=\sum_{i=0}^{k}C_{k}^{i}xi^{k-i}y^{i}\), \(C_{k}^{i}\)和\(y^{i}\)是相同的，只需要维护所有数的0到k次方之和即可

10.4 Dash Speed

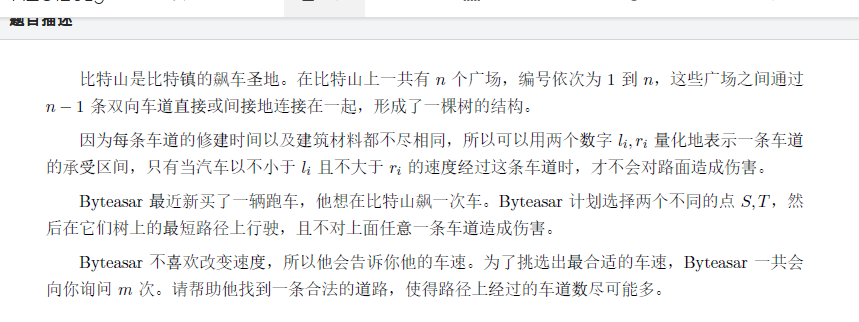
神仙题。。。 每条道路都有作用的一个范围，可以考虑线段树分治。线段树每个点开个vector，一条边的范围是[ql, qr], 则在线段树上被这个范围包含的节点加入这条边。
遍历整棵线段树，走到一个点，就把这个节点vector内所有的边加入到并查集，两个联通块合并，新的直径一定是第一个块的直径a,b第二个块的直径c,d其中的两个点为端点，可以通过反证法来证明。到了叶子节点，就得到了这个点的答案，然后回溯，需要把不属于该范围内的边删除，可以开一个栈，一步步的撤销就行了。

10.4 装饰

这种题好难想啊。。令a<b<c，若c>2（a+b），可以放的桌子数为a+b，放1个a放2个c，能把a放完，放1个b2个c，能把b放完。若c<2(a+b)，可以放的数量为(a+b+c)/3，可以先按1个b两个c放，放若干个，b如果少了就按1个a两个c放，一直这样放，可以使a=b，c-a<=2，再按1个a，1个b，1个c放即可。

10.4 凉宫春日的消失

10.5 小奇的仓库

虽然是个原题，但还是不会。异或的数很小，最多只能影响到数的后4为，定义f[i][j]为到i点后四位状态为j的路径条数，先求子树到根节点状态为j的路径条数，f[rt][(j+edge[j].dis)%16]+=f[v][j]，然后再通过根节点来更新儿子的子树之外的路径条数，这种思想已经用过很多次了，需要掌握。f[v][(j+edge[i].dis)%16) += f[rt][j] - f[v][[(j-edge[i].dis)+16)%16],但这样可能会影响到一些值，这个值又去更新其他的值，答案就错了，所以可以用个临时数组存一下，ans[i]表示其他点到i的路径总和，可以换根求，然后再累加状态为状态为j的路径条数×（j^m-j)即为答案。

10.5 征途堆积出友情的永恒

很容易想到f[i]=min(f[i], f[j]+max(sum[i]-sum[j],b[j])), 考虑优化。可以开两个堆，一个存f[j]+b[j], 一个存f[j]-sum[j],这样我们转移时，就可以比较两个堆顶的大小来得到f[i]。如果堆顶的编号在i-k之前，肯定是不合法的弹掉就行。对于一个数j，我们先把它放到第一个堆，如果f[j]+b[j]<f[j]+sum[i]-sum[j]，就把它从第一堆放到第二个堆，因为求的是max(sum[i]-sum[j],b[j])，sum的差值是在变大的，b[j]是不变的。这样维护即可。

射手座之日

考虑每加进去一个点，以当前点为右端点的区间的lca会怎么变化，很显然，新的lca肯定在当前点到根的路径上，先找到当前点和上一个点的lca，记为p点。若之前一些区间的lca就在p点以上，不需要管他，如果一些区间的lca在p点的子树里，肯定不能再算了，因为这个区间至少要经过当前点，上一个点，所以lca会变成p点，我们需要把p点子树出现过的lca次数转移到p点，按dfn序建线段树，维护子树点作为lca出现的次数，及次数乘权值之和。

甜圈

可以把每个点的任务看作一个字符串，线段树维护每个点的哈希值，判断是不是和要求的答案的哈希值相等。 （线段树如何维护区间乘法区间加法？先乘后加，如果乘mul=val,add=val,sum=val 如果加add+=val,sum+=lenval,下传时sum[son]=sum[son]mul[rt]+add[rt]len,add[son]=add[son]mul[rt]+add[rt],mul[son]=mul[son]mul[rt]，挺妙的）

LCA

一个点到根节点的经过的节点数是他的深度，其实也就相当于把它到根节点每个点的权值加个1，统计x和y的LCA的深度，可以让x到根节点的路径上的点权值加1，查询y到根节点的权值之和。询问有很多，都是区间的形式，可以考虑差分，把一个询问拆成两个，1个是1到l-1的点与z的lca深度之和，一个是1到r的点与z的lca深度之和，二者一减即可。

排序

神奇的思路。二分答案，若答案为mid，则把原序列大于等于mid的数设为1，否则为0，如果这样排序的话，其实就可以相当于是两次区间修改了，和之前做的一个题很像，那个好像也是给字母串排很多次序，字母只有26个，可以统计每个字母出现的次数，再区间修改。再看这个题，如果说第q个位置排完了序是1，说明答案肯定大于等于mid，否则答案小于mid。

逆序对的性质

一个序列进行冒泡排序，交换的次数也就是逆序对的数量。

luogu3531 LIT

将原序列从1到n从小到大编号，映射到另一个序列，求的是交换的次数，即为逆序对的总数

10.9 trade

这题好难想啊。建一个堆，每次把a[i]放进去，如果堆顶的值比a[i]小，ans+=a[i]-q.top()。 可这样贪心肯定不是最优解，考虑如何撤销。如果我们把b卖了，就再把b的a值放进去。一开始我们买了a卖了b，但发现买a卖c更值，于是我们再把b给买回来。

10.9 sum

这题太妙了，这种问题竟然可以用莫队解决。定义两个指针l，r， 通过打表观察，可以得到 s[i][j]=s[i][j-1]+C(i,j) s[i][j]=s[i-1][j]*2-c[i-1][j] 每次移动指针可以O(1)算出来答案变化了多少。

10.10graph

如果是树的话，从下往上处理答案，如果一个点有偶数个儿子，让他们任意两两配对，否则，让剩余的一个儿子和当前点到他父亲的边配对，这样只会让根节点最多有一条边不能配对。如果是一个图的话，也是一样的，先dfs搞一棵树，如果碰到返祖边的话，其实可以直接把他当成自己的儿子，剩下就一样了，可以开一个数组f[i]表示当前状态是谁和i匹配

interval 分块练习

分块好题，调死我了。如果说间隔大于sqrt(n)直接暴力加，否则算出每个块开始i加的位置，加的个数和加的值是多少，放到vector里，以后查询的时候如果是整块就直接加上整个块的和，如果是散块，就把当前块的vector都取出来，暴力把这个块里的点加上该加的值。细节好多啊这个题。vector取完要clear，如果间隔大于sqrt(n)时，在给原序列加的时候不要忘了给当前数所在的块也加上。

拓扑中 字典序最小 和 小的数尽量靠前 的区别

  字典序最小可以正向拓扑， 小的数尽量靠前应该求出反图的字典序最大的拓扑序，再反过来，不过这东西怎么证明啊？谁来教教我

考虑
6-1-3
\
7
/
2-4-5
小的数尽量靠前，应该让6先出，因为1就跟在6后面
字典序，应该让2先出，因为第一个数不是6就是2，而2字典序小于6
先这么理解吧，小数靠前=大数靠后
此外，一个排列p，让它的字典序最小，也就是让他的逆置换值为1的下标尽量小，在满足值为1的下标尽量小的情况下，让值为2的下标尽量小，以此类推。

10.11 虎

考场上贪心题基本上没做对过，问了问凯爹贪心题怎么做，他说如果是你要做这个决策，你该怎么做。可是我不知道啊。考场上不知道那种没有限制的边该和谁连。正解是把那种带限制的边缩掉，我不会。问了问soda，他的法挺好。我发现这个题和兔子和樱花挺类似。考虑一个节点与儿子以及父亲的关系，什么情况下一个节点和他父亲的边会被用到，如果这条边有限制而且是黑色，肯定就不会了。如果有偶数个儿子上传上来一条边，那么就让他们两两匹配，否则会剩下一个儿子，这样这个点Dfs结束后return 1表示需要它与父亲的边需要被染色。而如果一个点和儿子的边没有限制但是传上来了一条边，也把他算到合法的儿子里

10.11 陶陶摘苹果

用线段树维护包含第一个点的最长上升子序列。问题是怎么合并区间答案。记录区间的最大值Max和区间最长上升子序列的长度num。在pushup函数中，Max[rt]=两个儿子的Max。
左儿子肯定是都能看到的，左儿子最高的那个会把右儿子的一部分给挡住。记val为左儿子的最高点，然后我们需要查询右儿子，用一个query函数，如果当前区间最大值都比val小说明都会被挡住，直接返回0。如何在query函数中做到log的查询？如果左儿子的最高值比val小，肯定都看不到了，查询右儿子。否则，查询左儿子，右儿子怎么算？不是num[rs]
而是num[rt]-num[ls]，num[rs]是没有val限制下的长度，所以说右儿子的答案是num[rt]-num[ls]。当l=r时就看高度有没有val高就行了。不过我现在还不是很理解这东西
这题还有分块的写法，预处理每个点到最后会经过多少个点，然后就是如何找到比当前点大的坐标在当前点右侧且最小的那个数，可以分块，当前的块先扫一下有没有，如果没有的话，从左到右看哪个快最高的高度比当前点高，找到这个块再暴力扫一下就行。
还有一种二分的写法。可以st表预处理区间最大值，若把pos上的值改为val，让l=pos+1,r=n，二分mid，如果l到mid的最大值比val大，肯定要找左区间，否则找右区间，如果没有的话就返回一个值特判一下，比如返回n+1
唉，考场上就是没有想到怎么找第一个比他大的数，多积累经验吧

10.11 开心的金明

非常恶心的一道题，考场上这题部分分也不会打。原材料没有限制，其实可以预处理每天的原材料花费最小值，c[i]=min(c[i-1]+r[i-1],c[i])，这一天花费最小，要不就是之前买的加上存储的费用，要不就是这一天买的费用，取个min就行。可以用一个堆，先把这一天能买的电脑都买了，放到堆里，然后考虑用把电脑花费最小的拿出来，满足需求。如果一些电脑还有剩余就先在数组存一下，电脑只能存e[i]个，把多余的电脑给卖掉，肯定是把花费大的先卖了。然后再重新把剩余的物品入堆，存电脑需要E[i]元，所以把价值顺便加上。最后ans+=left*E[i]