字符串的几个题
1
 ||
||
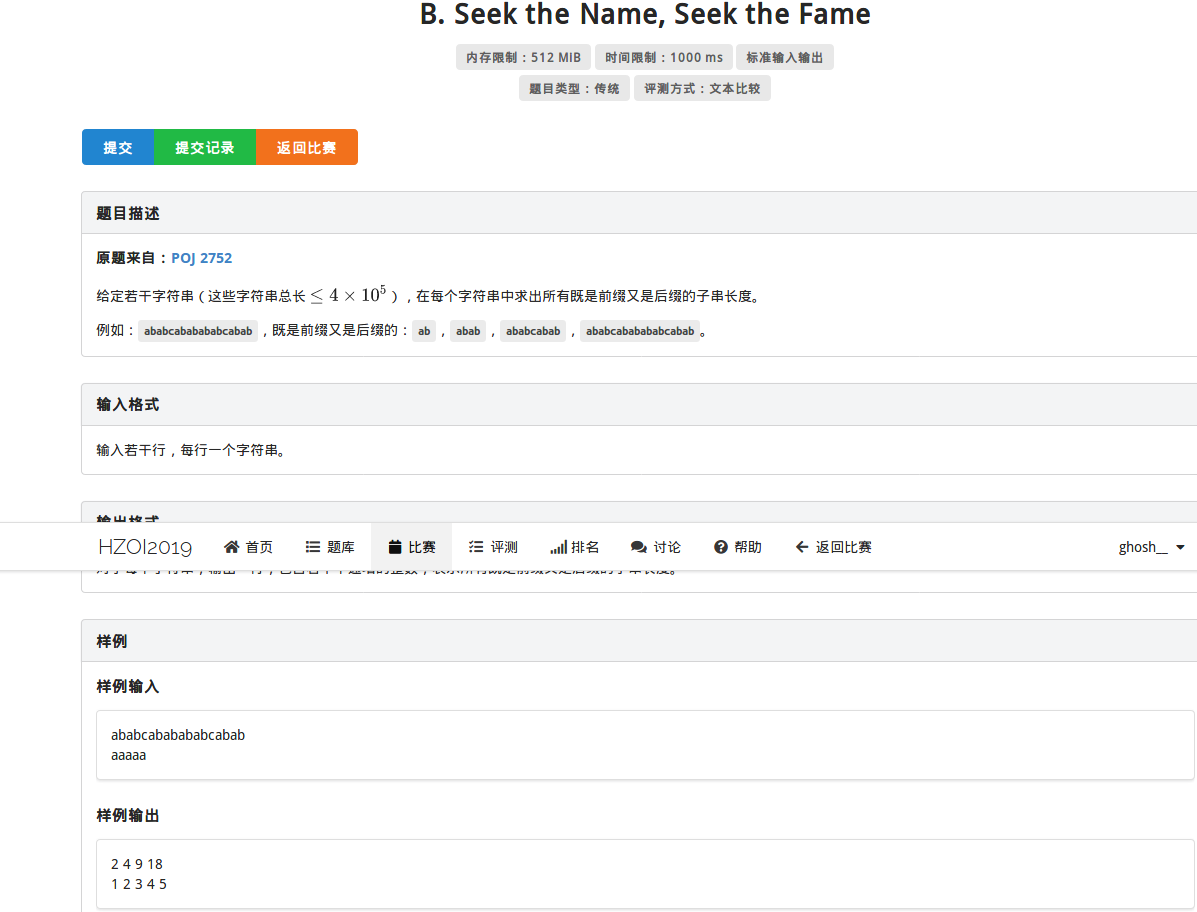
思路
枚举长度前缀和后缀的长度,再判断前缀和后缀的哈希值相不相等就好了
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 4e5 + 5;
typedef unsigned long long ull;
ull p[maxn], hash[maxn];
ull base = 131;
int lena;
char a[maxn], b[maxn];
ull GetHash(int l, int r) {
return hash[r] - hash[l - 1] * p[r - l + 1];
}
int main() {
while (scanf("%s", a + 1) != EOF) {
lena = strlen(a + 1);
p[0] = 1;
for (int i = 1; i <= lena; i++)
hash[i] = hash[i - 1] * base + a[i] - 'a' + 1,
p[i] = p[i - 1] * base;
for (int i = 1; i <= lena; i++) {
if (GetHash(1, i) == GetHash(lena - i + 1, lena)) {
printf("%d ", i);
}
}
printf("\n");
}
}
2
(图片怎么发不上去啊??)
//动物园
题目描述
近日,园长发现动物园中好吃懒做的动物越来越多了。例如企鹅,只会卖萌向游客要吃的。为了整治动物园的不良风气,让动物们凭自己的真才实学向游客要吃的,园长决定开设算法班,让动物们学习算法。
某天,园长给动物们讲解KMP算法。
园长:“对于一个字符串SSS,它的长度为LLL。我们可以在O(L)O(L)O(L)的时间内,求出一个名为next的数组。有谁预习了next数组的含义吗?”
熊猫:“对于字符串SSS的前iii个字符构成的子串,既是它的后缀又是它的前缀的字符串中(它本身除外),最长的长度记作next[i]next[i]next[i]。”
园长:“非常好!那你能举个例子吗?”
熊猫:“例SSS为abcababc,则next[5]=2next[5]=2next[5]=2。因为SSS的前555个字符为abcab,ab既是它的后缀又是它的前缀,并且找不到一个更长的字符串满足这个性质。同理,还可得出next[1]=next[2]=next[3]=0next[1] = next[2] = next[3] = 0next[1]=next[2]=next[3]=0,next[4]=next[6]=1next[4] = next[6] = 1next[4]=next[6]=1,next[7]=2next[7] = 2next[7]=2,next[8]=3next[8] = 3next[8]=3。”
园长表扬了认真预习的熊猫同学。随后,他详细讲解了如何在O(L)O(L)O(L)的时间内求出next数组。
下课前,园长提出了一个问题:“KMP算法只能求出next数组。我现在希望求出一个更强大num数组一一对于字符串SSS的前iii个字符构成的子串,既是它的后缀同时又是它的前缀,并且该后缀与该前缀不重叠,将这种字符串的数量记作num[i]num[i]num[i]。例如SSS为aaaaa,则num[4]=2num[4] = 2num[4]=2。这是因为SSS的前444个字符为aaaa,其中a和aa都满足性质‘既是后缀又是前缀’,同时保证这个后缀与这个前缀不重叠。而aaa虽然满足性质‘既是后缀又是前缀’,但遗憾的是这个后缀与这个前缀重叠了,所以不能计算在内。同理,num[1]=0,num[2]=num[3]=1,num[5]=2num[1] = 0,num[2] = num[3] = 1,num[5] = 2num[1]=0,num[2]=num[3]=1,num[5]=2。”
最后,园长给出了奖励条件,第一个做对的同学奖励巧克力一盒。听了这句话,睡了一节课的企鹅立刻就醒过来了!但企鹅并不会做这道题,于是向参观动物园的你寻求帮助。你能否帮助企鹅写一个程序求出num数组呢?
特别地,为了避免大量的输出,你不需要输出num[i]num[i]num[i]分别是多少,你只需要输出所有(num[i]+1num[i]+1num[i]+1)的乘积,对1,000,000,0071,000,000,0071,000,000,007取模的结果即可。
输入格式
第111行仅包含一个正整数nnn ,表示测试数据的组数。
随后nnn行,每行描述一组测试数据。每组测试数据仅含有一个字符串SSS,SSS的定义详见题目描述。数据保证SSS 中仅含小写字母。输入文件中不会包含多余的空行,行末不会存在多余的空格。
输出格式
包含 nnn 行,每行描述一组测试数据的答案,答案的顺序应与输入数据的顺序保持一致。对于每组测试数据,仅需要输出一个整数,表示这组测试数据的答案对 1,000,000,0071,000,000,0071,000,000,007 取模的结果。输出文件中不应包含多余的空行。
输入输出样例
输入 #1
3
aaaaa
ab
abcababc
输出 #1
36
1
32
说明/提示
测试点编号 约定
1 N≤5,L≤50N ≤ 5, L ≤ 50N≤5,L≤50
2 N≤5,L≤200N ≤ 5, L ≤ 200N≤5,L≤200
3 N≤5,L≤200N ≤ 5, L ≤ 200N≤5,L≤200
4 N≤5,L≤10,000N ≤ 5, L ≤ 10,000N≤5,L≤10,000
5 N≤5,L≤10,000N ≤ 5, L ≤ 10,000N≤5,L≤10,000
6 N≤5,L≤100,000N ≤ 5, L ≤ 100,000N≤5,L≤100,000
7 N≤5,L≤200,000N ≤ 5, L ≤ 200,000N≤5,L≤200,000
8 N≤5,L≤500,000N ≤ 5, L ≤ 500,000N≤5,L≤500,000
9 N≤5,L≤1,000,000N ≤ 5, L ≤ 1,000,000N≤5,L≤1,000,000
10 N≤5,L≤1,000,000N ≤ 5, L ≤ 1,000,000N≤5,L≤1,000,000
思路
这个题的话,先考虑暴力怎么做。
如果要写暴力的话,先处理出来next数组,对于每个i,先把j跳到\(\frac{i}{2}\)之前的地方,再让j开始跳,即j=next[j],每跳一次,cnt++。这样就得到了num[i]
不过这样肯定会超时,要想想如何优化。
先考虑可以重叠的情况,我们知道next[i]是i的最长公共前后缀,next[next[i]]是next[i]的最长公共前后缀,很显然num[i] = num[next[i]]+1,这个多出来的1就是next[i]本身
如果不重叠,我们让j往前跳,一直到2*j<=i,这样num[i]就是num[j]+1了,因为j是前后缀不会重叠的最大的一个。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
const int MOD = 1e9 + 7;
const int maxm = 1e4 + 5;
int lena, lenb, next[maxm], f[maxn], num[maxn];
char a[maxn], b[maxn];
int main() {
int T;
cin >> T;
while (T--) {
memset(next, 0, sizeof(next));
scanf("%s", a + 1);
lena = strlen(a + 1);
num[1] = 1;
for (int i = 2, j = 0; i <= lena; i++) {
while (j && (a[i] != a[j + 1])) j = next[j];
if (a[i] == a[j + 1]) next[i] = ++j;
num[i] = num[j] + 1;
}
long long ans = 1;
for (int i = 2, j = 0; i <= lena; i++) {
while (j && (a[i] != a[j + 1])) j = next[j];
if (a[i] == a[j + 1]) j++;
while ((j * 2) > i) j = next[j];
ans = ans * (num[j] + 1);
ans %= MOD;
}
printf("%lld\n", ans);
}
return 0;
}
3
//okr
题目描述
一个串是有限个小写字符的序列,特别的,一个空序列也可以是一个串. 一个串P是串A的前缀, 当且仅当存在串B, 使得 A = PB. 如果 P!=A 并且 P 不是一个空串,那么我们说 P 是A的一个proper前缀. 定义Q 是A的周期, 当且仅当Q是A的一个proper 前缀并且A是QQ的前缀(不一定要是proper前缀). 比如串 abab 和 ababab 都是串abababa的周期. 串A的最大周期就是它最长的一个周期或者是一个空串(当A没有周期的时候), 比如说, ababab的最大周期是abab. 串abc的最大周期是空串. 给出一个串,求出它所有前缀的最大周期长度之和.
输入格式
第一行一个整数 k ( 1 k 1 000 000) 表示串的长度. 接下来一行表示给出的串.
输出格式
输出一个整数表示它所有前缀的最大周期长度之和.
样例输入
8
babababa
样例输出
24
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
做这个题真的跟做阅读理解似的,贴一下洛谷上某位大佬写的题意
对于一个仅含小写字母的字符串a, p为a的前缀且p!=a,那么我们称p为a的proper前缀.
规定字符串Q(可以是空串)表示a的周期,当且仅当Q是a的proper前缀且a是Q+Q的前缀,
例如 ab是abab的一个周期,因为ab是abab的proper前缀,且abab是ab+ab的前缀.
求给定字符串所有前缀的最大周期长度之和.
思路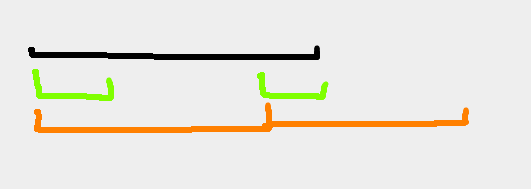
黑色线段为原字符串(长度为l1),绿色为其中的一段公共前后缀(长度为l2),可以发现橙色线段就是周期Q,(长度为l1-l2),因为第二段Q的开头一直到原字符串的最后是这段字符串的后缀,也等于这段字符串的前缀(绿色线段),恰好可以接上。对于每个i,需要找到长度最小的公共前后缀,这个过程可以记忆化一下。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
int n, next[maxn];
char a[maxn];
int main() {
scanf("%d", &n);
scanf("%s", a + 1);
for (int i = 2, j = 0; i <= n; i++) {
while (j && a[i] != a[j + 1]) j = next[j];
if (a[i] == a[j + 1]) next[i] = ++j;
}
long long ans = 0;
for (int i = 1, j; i <= n; i++) {
j = i;
while (next[j]) j = next[j];
if (next[i]) next[i] = j;
ans += i - j;
}
cout << ans;
return 0;
}
4
//phone list
题目
给定nnn个长度不超过101010的数字串,判断是否有两个字符串AAA和BBB,满足AAA是BBB的前缀,若有,输出NO,若没有,输出YES。
输入 #1
2
3
911
97625999
91125426
5
113
12340
123440
12345
98346
输出 #1
NO
YES
思路
数据量很大,问s是不是t的前缀,可以通过建trie树的方法做
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
int trie[maxn][11], tot, len, last[maxn], flag;
int n, vis[maxn], rt;
void Insert(char *s) {
len = strlen(s + 1);
rt = 0;
for (int i = 1; i <= len; i++) {
int id = s[i] - '0';
if (!trie[rt][id])
trie[rt][id] = ++tot, vis[rt] = 1;
if (last[rt]) {
flag = 0;
return;
}
rt = trie[rt][id];
}
if (vis[rt]) flag = 0;
last[rt] = 1;
return;
}
int main() {
int T;
cin >> T;
while (T--) {
tot = 0;
flag = 1;
memset(trie, 0, sizeof(trie));
memset(last, 0, sizeof(last));
memset(vis, 0, sizeof(vis));
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
char s[14];
scanf("%s", s + 1);
if (flag) Insert(s);
}
if (flag) puts("YES");
else puts("NO");
}
return 0;
}
。。。。。。。。。。。。。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号