数制的转换
由于最近在帮忙复习计算机一级考试题目,有做到数制转换的题目,故而复习了一遍大学曾经学过的数制转换,觉得数制的转换其实还是挺重要的(曾经面试.net开发的时候面试题有出现类似的题目了),下面我来讲解一下我自己对数制转换的理解。
十进制 → (二、八、十六进制)
十进制 → 二进制
二进制数主要是有0和1组成的数值,十进制数转二进制数主要是通过除二取余的方式,以数字100为例子:

如上图所示,通过100除以2,直到除尽为止,最终得到的余数翻转过来,就是该十进制数的二进制数了,所以得到100的二进制数为1100100。
十进制 → 八进制
八进制数主要是由0到7八位数组成,逢八进一,十进制转八进制数主要是通过除八取余的方式,
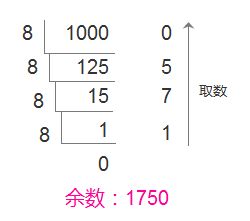
十进制 → 十六进制
十六进制数主要是由0到9,A到F(或a到f)十六位数组成,A到F表示数值10到15,逢十六进一,十进制转十六进制数主要是通过除十六取余的方式,
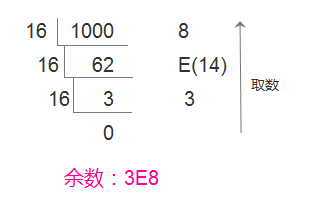
总结下来,十进制转二、八、十六进制的方法十分雷同,只要通过除以相对应的进制数,将取得的余数从下往上读取,即可读取到要转换的数值了。
(二、八、十六进制) → 十进制
二进制 → 十进制
相信上面的例子已经能够很直观的知道十进制数转换成二进制数的规则了(我认为图片比较直观点~~)。那么,由二进制又如何转换成十进制数呢?
还是以100的二进制数1100100为例子,则转换计算公式为:
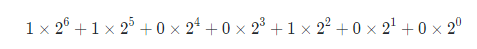
可以看出,1100100一共有7位二进制数,所以转换要计算的是2的最高幂数是6,然后按位递减并且按位相乘,我们可以简化公式为:
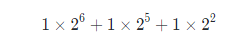
八进制 → 十进制
以八进制数12345670为例子,将数值转换为十进制,计算公式为:
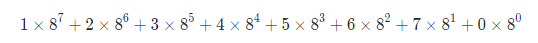
十六进制 → 十进制
以十六进制数2A8E9D为例子,将数值转换为十进制,计算公式为:
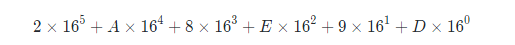
同十进制数转其他进制数的规律,转换的方式是按位乘以16的幂,按位数降幂的方式进行计算,通过观察三种计算方式的公式能总结出这个规则。
二进制 → (八、十六进制)
二进制 → 八进制
八进制的数和二进制数可以按位对应(八进制一位对应二进制三位),下表是二进制/八进制换算表
| 二进制 | 八进制 |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
因为是每三位二进制数代表了一位八进制数,以11001101010101为例子,由低位开始分割,每隔三位数分割一次,得到下面的分割式子:
011 | 001 | 101 | 010 | 101
当分割到高位时,发现不足三位,则在最高位开始补0,直到满足三位为止,如果能记住上面的转换表,我们能够快速地转换,直接转换后按顺序合并的结果就是转换结果,所以对上表得出转换结果为:
011 | 001 | 101 | 010 | 101 = 3 1 5 2 5
二进制 → 十六进制
二进制和十六进制数的对应规则是一位十六进制的数值对应四位的二进制数值,如:
4=0100;
7=0111;
A=1010;
以10001111010为例子:
0100 | 0111 | 1010 = 4 7 A
(八、十六进制) → 二进制
八进制 → 二进制
规则:按照顺序,每1位八进制数改写成等值的3位二进制数,次序不变。
例子:345 = 011 100 101
十六进制 → 二进制
规则:按照顺序,每位十六进制数对应的是四位的二进制数,次序不变。
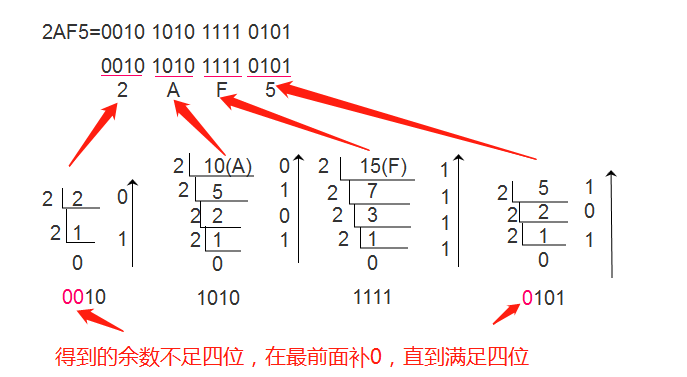
例子:2AF5=0010 1010 1111 0101
将二进制数转换为八、十六进制,总结以上例子,是相似的规则,按位计算每个位数数值的二进制数,然后按顺序合并起来,得到最终的结果,下图是十六进制每一位数的计算方式,八进制的每一位也是根据同样的规则计算得到。
八进制 ↔ 十六进制
八进制和十六进制之间是没有直接转换的公式,只能通过十进制或二进制为中间转换数制进行转换,而前面我已经把各种类型之间的数制转换方式都描述了,这里我就不在描述一遍了。
以上的转换规则相信只要多测试几个数字应该都能立即其中的原理,如果实在不懂还是建议多动手计算,我个人还是比较相信自己亲手验证过的东西~~
模二运算法则
十进制数的加减乘除我们统称为四则运算,那么二进制数的加减乘除又叫什么呢?相信从标题能够看出,没错,就叫模二运算法则,分别成模二加法、模二减法、模二乘法、模二除法,下面主要讲解下四种法则的运算规则:
模二加法
与十进制的加法不同,模二加法不需要进位,计算规则为:① 1+1=0+0=0;② 1+0=0+1=1。
以[1101]+[111]+[101]=[1111]为例子:
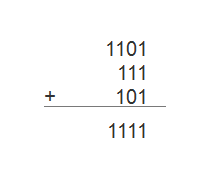
在百度百科中还有一个重要的结论:奇数个1相加得1,偶数个1相加得0。
模二减法
与模二加法同理,模二减法不需要借位,计算规则为:① 1-1=0-0=0;② 1-0=0-1=1。
下面我们以[101101]-[001010]=[100111]为例子:

对比模二加法,是不是发现规则和模二加法的规则一样?是的,模2加法和模2减法实际上是一回事,所有用模2减法的地方都可用模2加法来代替。
模二乘法
模二乘法和十进制的乘法步骤十分类似,但是计算规则依然类似于模二加/减法:① 0×0=1×1=0;② 1×0=0×1=1;
下面以[1001]×[1101]=[1100101]为例子:
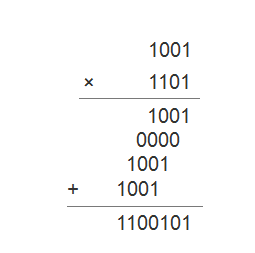
模二除法
模二除法是我认为在模二运算法则中最复杂的一个运算,这里我没有画图表示,因为我觉得我目前理解的画出来的图可能还不能够让人深刻理解,但是这里我引用了别人的一篇博客,我觉得写得很直观易懂大家可以去看看:模2除法(CRC校验码计算)。
模2除法是模2乘法的逆运算。想知道模2除法,需要知道什么是异或运算。
计算机中,异或逻辑表示为: (记忆方法:同为0异为1)
1^1=0
0^0=0
1^0=1
0^1=1
模2除法具有下列三个性质:
- 当最后余数的位数小于除数位数时,除法停止。
- 当被除数的位数小于除数位数时,则商数为0,被除数就是余数。
- 只要被除数或部分余数的位数与除数一样多,且最高位为1,不管其他位是什么数,皆可商1。
模2算术是编码理论中多项式运算的基础。模2算术在其他数字领域中的应用也是很广泛的。
本文仅是个人对数制转换的理解而写的,也有可能理解的有不足之处,还望指出。





