7 顺时针打印矩阵

0 引言

题目：输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵：

1     2     3    4

5     6     7    8

9     10    11   12

13    14    15   16 ，

则依次打印出数字 1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

1 抽象问题具体化

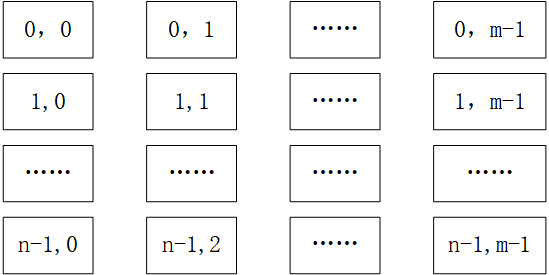
打印顺序为：

1）最外圈，一直到最里圈，一圈一圈地打印；

2）最外圈的打印顺序为：左上角到右上角，右上角到右下角，右下角到左下角，左下角到左上角 　　

举例1：

{1}，输出{1}

举例2：

{{1，2}，{3，4}}，输出{1，2，4，3}

举例3：

{1，2，3，4，5}，输出{1，2，3，4，5}

举例4：

{{1}，{2}，{3}，{4}，{5}}，输出{1，2，3，4，5}　　

2 具体问题抽象分析

 （1）外循环：

圈子在往里边缩，需要直到圈子的四个边界值，分别是：

最外圈为第0圈：行坐标范围是（0，n-1），列坐标范围是（0，m-1）

里边的圈子为：已知当前为第p圈，行坐标（p，n-1-p），列坐标范围是（p，m-1-p）

（2）内循环：

圈子从（p，p）点开始，一直打印到（m-1-p，n-1-p）

 分四行打印，如图所示。

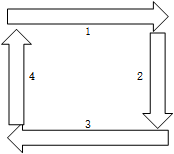
1）第一行一定要打印

2）第二行打印条件：行数大于2

3）第三行打印条件：行数大于1

4）第四行打印条件：行数大于2而且列数大于1

（3）考虑特殊情况：

当矩阵行数等于0时，直接返回空向量即可

3 demo 

   vector<int> printMatrix(vector<vector<int> > matrix) {
        vector<int> myMatrix;
        myMatrix.clear();
        if(matrix.size() == 0)  // 正负性
            return myMatrix;
        int n = matrix.size();     // 行数
        int m = matrix[0].size();  // 列数
        int p = 0;           //圈数，将最外圈定义为第0圈
        int maxCircle = (float)min(n,m)/2 > (int)min(n,m)/2? (int)min(n,m)/2 
            + 1: (int)min(n,m)/2;        
        // 外循环
        for(;p < maxCircle; p ++){
            // 内循环
            // 从左上到右上，第一行  第一行是一定要打印出来的
            for(int x = p, y = p;y <=m-1-p;y++)
                myMatrix.push_back(matrix[x][y]);
            // 从右上到右下，第二行打印的条件是行数大于2  行数公式为 row = n-2*p
            if(n-2*p >2){
                for(int x = p+1, y = m-1-p; x < n-1-p;x++)
                    myMatrix.push_back(matrix[x][y]);
            }
            // 从右下到左下,第三行打印的条件是行数大于1
            if(n-2*p >1){
                for(int x = n-1-p, y = m-1-p; y>= p;y--)
                    myMatrix.push_back(matrix[x][y]);
            }
            // 从左下到左上，第四行打印的条件是行数大于2而且列数大于1
            if(n-2*p >2 && m-2*p >1){
                for(int x = n-1-p-1,y=p; x>p;x--)
                    myMatrix.push_back(matrix[x][y]);
            }                
        }
        return myMatrix;
    }

4 代码优化