循环不变式（loop invariants）不只是一种计算机科学的思想，准确地说是一种数学思想。在数学上阐述了通过循环（迭代、递归）去计算一个累计的目标值的正确性。
比如插入排序，每次循环从数组A中取出第j个元素插入有序区A[1 .. j-1]，然后递增j。这样A[1 .. j-1]的有序性始终得到保持，这就是所谓的“循环不变”了。
循环不变式主体是不变式，也就是一种描述规则的表达式。其过程分三个部分：初始，保持，终止。
1、初始：保证在初始的时候不变式为真。
2、保持：保证在每次循环开始和结束的时候不变式都为真。
3、终止：如果程序可以在某种条件下终止，那么在终止的时候，就可以得到自己想要的正确结果。
在这三个部分中，前两个是条件，最有一个是结论。
利用循环不变式(loop invariant)来证明循环的正确性与用数学归纳法(induction)证明数学等式的相同点在于：
都需要验证初值，或初始状态是否满足条件。
之后再证明在归纳或递推的过程中仍然满足这种条件。（这个条件在数学归纳中叫做递推关系，在循环中就是循环不变式(loop invariant)）。
循环不变式(loop invariant)与数学归纳法(induction)的区别在于：
数学归纳可能是无限的，是无限地腿的，但循环不变式所要证明的循环是要结束并给出正确结果的。
如何找循环不变式？
由于算法是一步步执行的，那么如果每一步（包括初试和结束）都满足一个共同的条件，那么这个条件就是要找的循环不变式（loop invariant）。
例子：
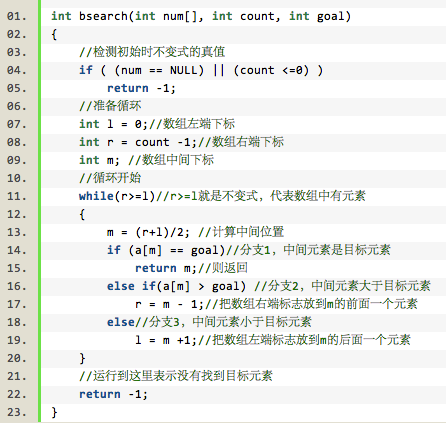
问题：给出二分查找的实现,函数原形 int bsearch(int num[], int count, int goal);
num是保存已经从小到大排序好的数字，count是数组元素个数，goal是待查找的数字；
若查找成功则返回元素的下标，否则返回-1。
分析：二分查找的原理很简单：
把数组分成三份，中间一份只有一个元素，其他两份个数基本相同，如果中间的元素等于目标值，就返回它的下标；
如果大于，则去前半数组继续执行二分查找；
如果小于，则去后半数组；
直到数组没有元素为止。
这是循环不变式的一个计算机算法应用，我们可以按照它的规则来做，
我们的不变式就是：当前数组不为空；
循环结束条件是：当前数组为空或找到目标元素。
例子2： 插入排序
当算法进行到第1行时，数组A中从第1个至第j-1个元素仍然是算法执行前数组中第1个至第j-1个元素，只是执行算法后，这些元素是排好序的，以上就是这个算法的for循环的循环不变式。(就是一个条件。)
在循环的Initialization阶段，j的初值为2，数组A[1 .. j-1]即是A[1],是排好序的，而且其元素仍然是原数组A[1]的，只是现在排好序了。
Maintenance：这个阶段要证明的是每一次循环的结果都满足先前提到的的循环不变式。
Termination：这个阶段要证明,当循环结束时，数组A中的所有元素都排好序。
再看算法第1行，当j=length[A]+1时循环结束，由于满足循环不变式，所以，数组A[1 .. length[A]]是排好序的，且是原数组的那些元素。
这里要得到的结果是排序且元素不改变的数组，所以循环不变式就是数组A中从第1个至第j-1个元素是排好序的且是与原数组的元素是一致的。
例子3：冒泡排序
伪代码：
BubbleSort(A[1..n])
1 for i= 1 to n
2 for j= n downto i+1 do
3 if A[j]<A[j-1]
4 exchange A[j] with A[j-1]
冒泡排序的工作原理为重复地交换相邻的两个反序元素。比如一个数组A[4]={1,3,5,2,},把里面的数进行从小到大的升幂排序。
（1，3），（3,5),(5,2)。这是第一次遍历后得到A[4]={1,3,2,5},
然后进行第二次遍历（1，3），（3，2），（2，5）后得到A[4]={1,2,3,5},
看到那个2了吧，不断往前冒，即冒泡。
算法简单是简单但要证明它的正确性却不是那么容易的。
设A为f(A)的输出。为了证明算法是正确的，需要证明它能够终止，并且有：A[1]<=A[2]<=....<=A[n-1]
要想完整的证明它的证明性，还必须要证明它的内层循环的正确性，然后再证明外层循环。
第一部分：内循环
对于2~4行的for循环，其任务是找出数组A[j..n]中最小的数字，并把这个数字移动到数组最前面。即有循环不变式：
每次迭代之前，A[j]=min{A[k] | j<=k<=n}，并且子数组A[j..n]中的元素还是最初在A[j..n]中的元素。
初始化：第一次迭代之前j=n，子数组A[j..n]只包含一个元素A[n]，循环不变式显然成立。
保持：迭代一个给定值的j。首先假设此次迭代前循环不变式成立，那么根据循环不变式，A[j]是A[j..n]中最小的元素。第3~4行代码表示如果A[j]<A[j-1]就交换A[j]和A[j-1]，显然这使得A[j-1]成为A[j-1..n]中最小的元素。由于唯一改变子数组A[j-1..n]的操作仅仅是那次可能发生的交换操作，且在迭代开始时，A[j..n]中的元素最初都是在A[j..n]中，所以在迭代开始时A[j-1..n]中的元素最初都是在A[j-1..n]中。然后j自减，准备开始进入下一轮迭代。
终止：循环终止时j=i。根据循环不变式，A[j]=A[i]=min{A[k] | i<=k<=n}，并且A[i..n]中的元素最初都在A[i..n]中。
所以在2~4行的for循环执行结束过后，A[i]将是A[i..n]中最小的元素。
第二部分：外循环
对于1~4行的for循环，其任务是对数组A[1..i]按照从小到大排序。 有循环不变式：
每次迭代之前，子数组A[1..i-1]包含了A[1..n]中前i-1小的所有元素，并且它们是已排好序的。A[i..n]中包含了A[1..n]中余暇的元素。
初始化：第一次迭代之前i=1。子数组A[1..i-1]为空，循环不变式显然成立。
保持：迭代一个给定值的i。首先假设此次迭代前循环不变式成立，那么根据循环不变式，A[1..i-1]包含了A[1..n]中前i-1小的所有元素，并且它们是已排好序的。第一部分已经证明：在执行2~4行的for循环后A[i]是A[i..n]中最小的元素。所以在执行了2~4行的for循环后A[1..i]中就包含了A[1..n]中前i小的所有元素，并且它们已经排好序。子数组A[i+1..n]就包含了n-i个A[1..n]中余下的元素。
终止：循环终止时i=n+1 => i-1=n。所以根据循环不变式，A[1..i-1]óA[1..n]中包含了A[1..n]中前i-1小的元素（即A[1..n]的全部元素），并且它们是排好序的。
所以在1~4行的for循环执行结束过后，A[1..n]将是有序的。
根据第二部分的结论，外层for循环结束后，数组A[1..n]中的元素将是排好序的。故冒泡排序算法是正确的。
参考资料：
http://blog.csdn.net/xieyuntestshow/article/details/7028824
http://baike.baidu.com/view/1368441.htm
http://blog.csdn.net/davelv/article/details/5952981
http://www.cnblogs.com/bamboo-talking/archive/2011/02/05/1950197.html
