概率论与数理统计图式(第四章 随机变量的数字特征)
概率论与数理统计图式(第四章 随机变量的数字特征)
1、随机变量的数学期望
(1)离散型随机变量数学期望

1)绝对收敛条件:打乱求和仍收敛,保证期望唯一。
2)随机变量的数学期望——随机变量取值对取值概率的加权平均。
(2)连续型随机变量数学期望

(3)特殊分布的数学期望
![]()
![]()
![]()

7、正态分布 E(X)=1/λ
8、柯西分布概率密度不存在(不收敛)
2、随机变量的函数的数学期望
1)求E(Y) 时,不必算出 Y的分布,只要直接利用 X 的分布进行计算就行了。(表达式无y)
2)随机变量函数的数学期望是常数, 代表了函数变量值对取值概率的加权平均值
3)推广至二维


3、随机变量的数学期望的性质
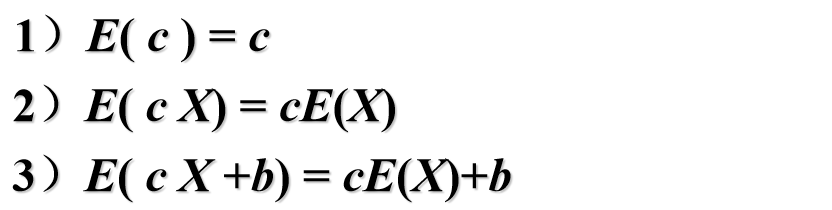
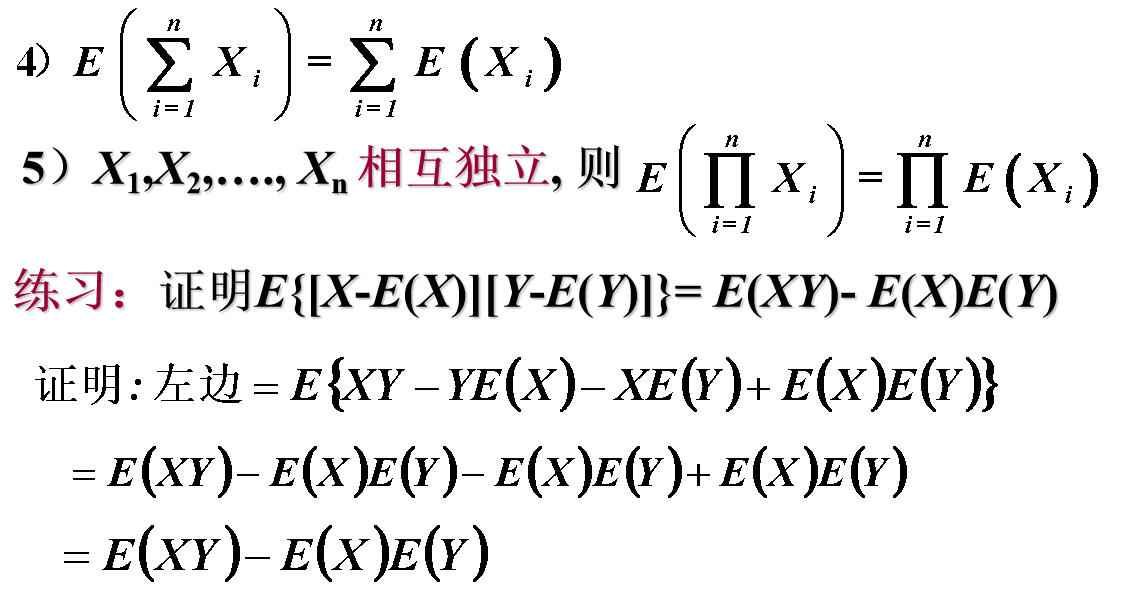
4、随机变量的方差
(1)方差定义
![]()
1)方差刻划了随机变量X 对其数学期望的偏离程度!
2)物理意义:对分布律对应的单位质量离散质点系统
- 数学期望为系统的质心
- 方差为质点系统相对于其质心所在纵轴的转动惯量
(2)常见随机变量的方差![]()
![]()
![]()
![]()
![]()
![]()
5、随机变量的数学期望的性质

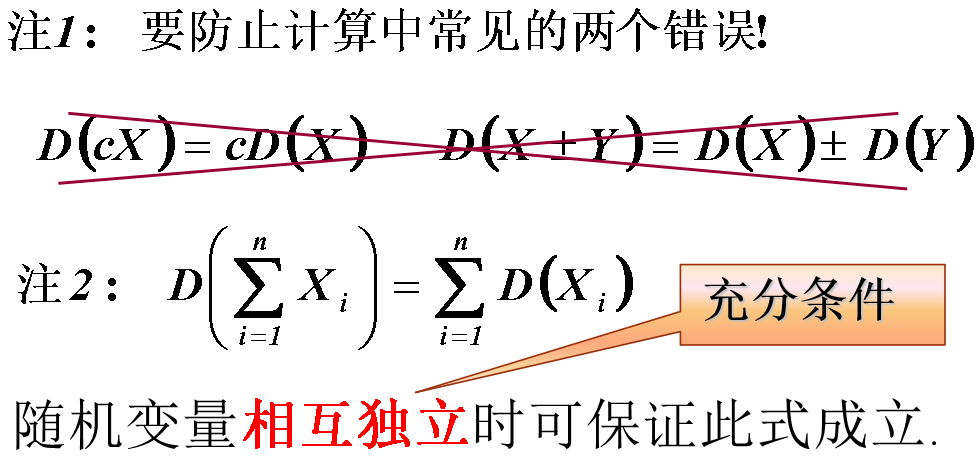

6、协方差,相关系数与矩

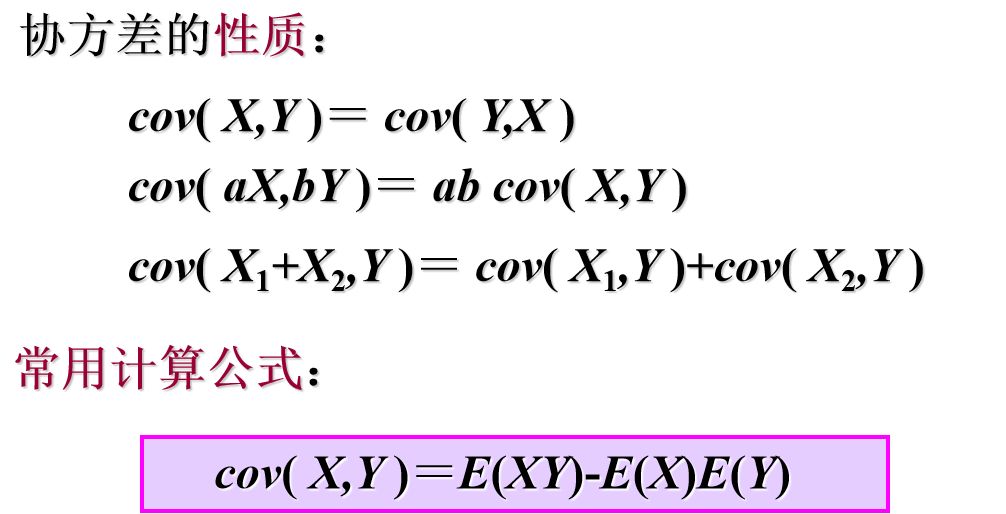


PS:
- 相关系数是为了消除X、Y的量纲
- 相关系数是标准化随机变量的协方差
- X*为标准化随机变量:期望为0,方差为1
- 最后一步因常用式中X、Y的期望为0,只剩下相关系数一项

- 以概率1线性相关,及允许少量点不在直线上

- 线性变换不改变相关系数大小/不改变变量线性相程度


- 不相关:不线性相关(也是有关系的)





