排序04--[快速排序&&希尔排序]

1.快速排序(Quick Sort)

1.1简介

 

 

 1.2执行流程

 

 

 1.3快速排序--轴点的构造

 

 

 1.4快速排序--时间复杂度

 

 

 1.5快速排序--实现

 

 

 

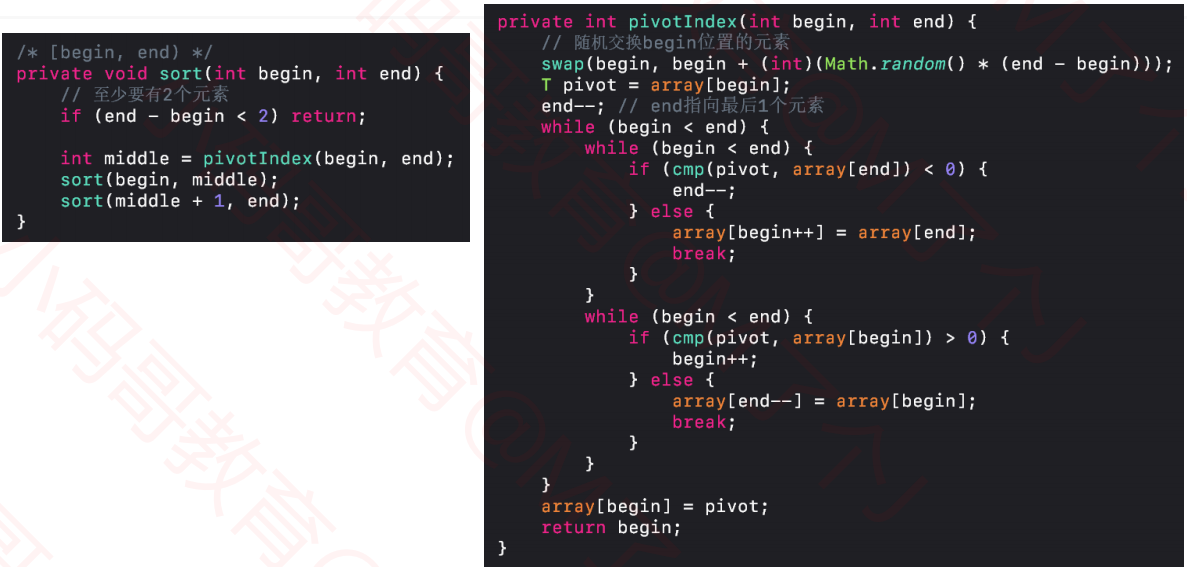
@Override
    protected void sort() {
        sort(0, array.length);
    }

    /**
     * 对 [begin, end) 范围的元素进行快速排序
     * @param begin
     * @param end
     */
    private void sort(int begin, int end) { 
        if (end - begin < 2) return;
        
        // 确定轴点位置 O(n)
        int mid = pivotIndex(begin, end);
        // 对子序列进行快速排序
        sort(begin, mid); 
        sort(mid + 1, end); 
    } 
    
    /**
     * 构造出 [begin, end) 范围的轴点元素
     * @return 轴点元素的最终位置
     */
    private int pivotIndex(int begin, int end) {
        // 随机选择一个元素跟begin位置进行交换
        swap(begin, begin + (int)(Math.random() * (end - begin)));
        
        // 备份begin位置的元素
        T pivot = array[begin];
        // end指向最后一个元素
        end--;
        
        while (begin < end) {
            while (begin < end) {
                if (cmp(pivot, array[end]) < 0) { // 右边元素 > 轴点元素
                    end--;
                } else { // 右边元素 <= 轴点元素
                    array[begin++] = array[end];
                    break;
                }
            }
            while (begin < end) {
                if (cmp(pivot, array[begin]) > 0) { // 左边元素 < 轴点元素
                    begin++;
                } else { // 左边元素 >= 轴点元素
                    array[end--] = array[begin];
                    break;
                }
            }
        }
        
        // 将轴点元素放入最终的位置
        array[begin] = pivot;
        // 返回轴点元素的位置
        return begin;
    }

 

1.6快速排序--与轴点相等的元素

 

 

 

 

 

 

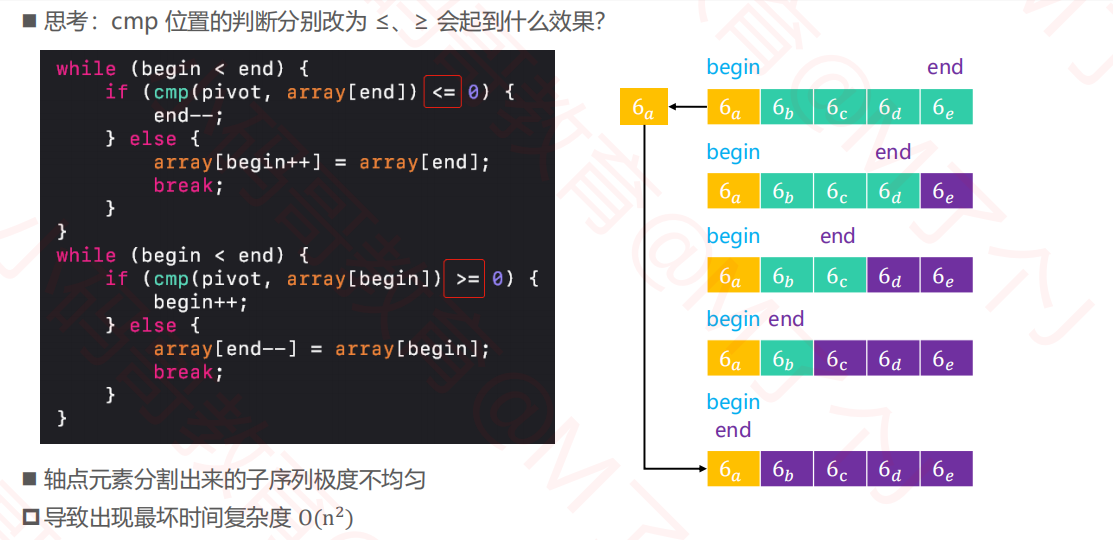
2.希尔排序(Shell Sort)

2.1简介

 

 

 2.2希尔排序--实例

 

 

 

 

 

 

 

 

 

 

 

 

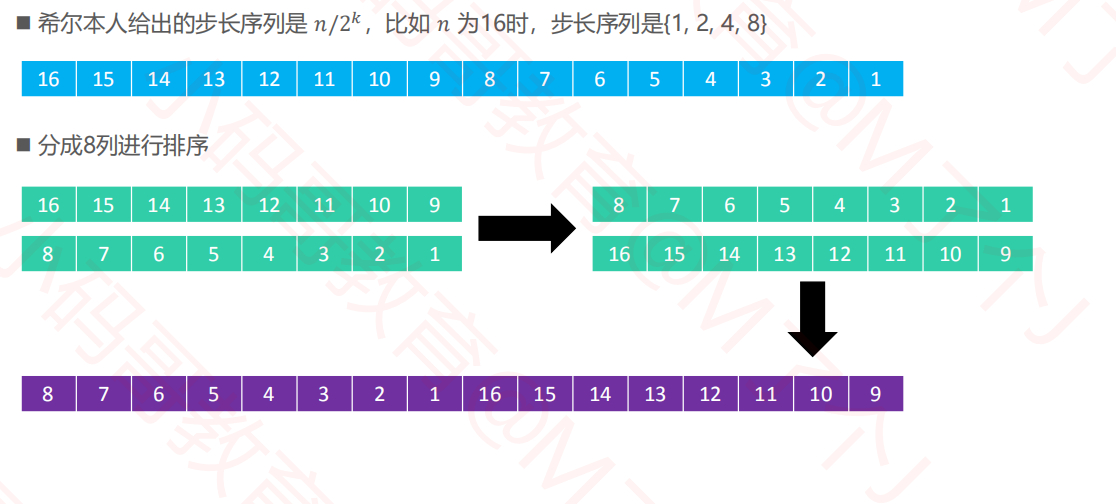
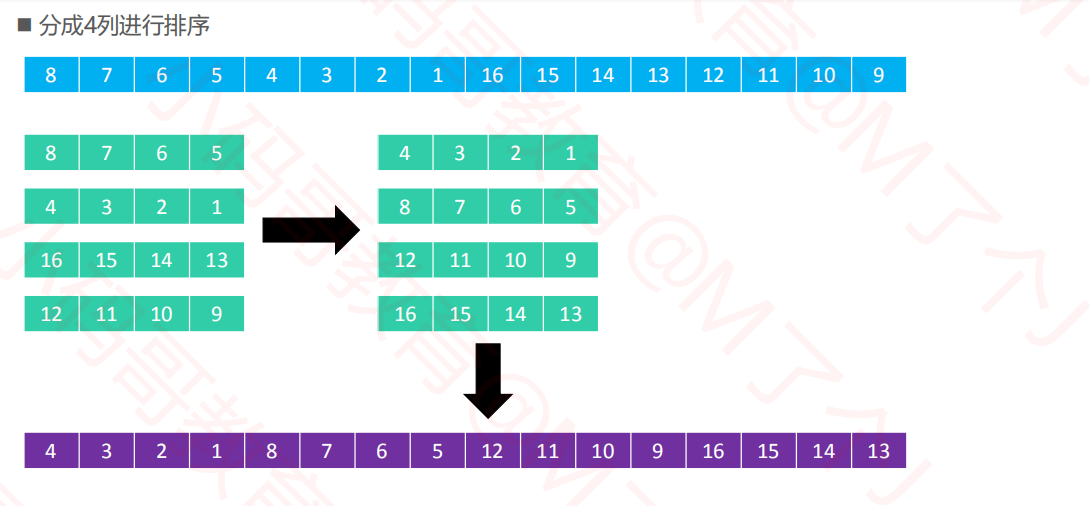
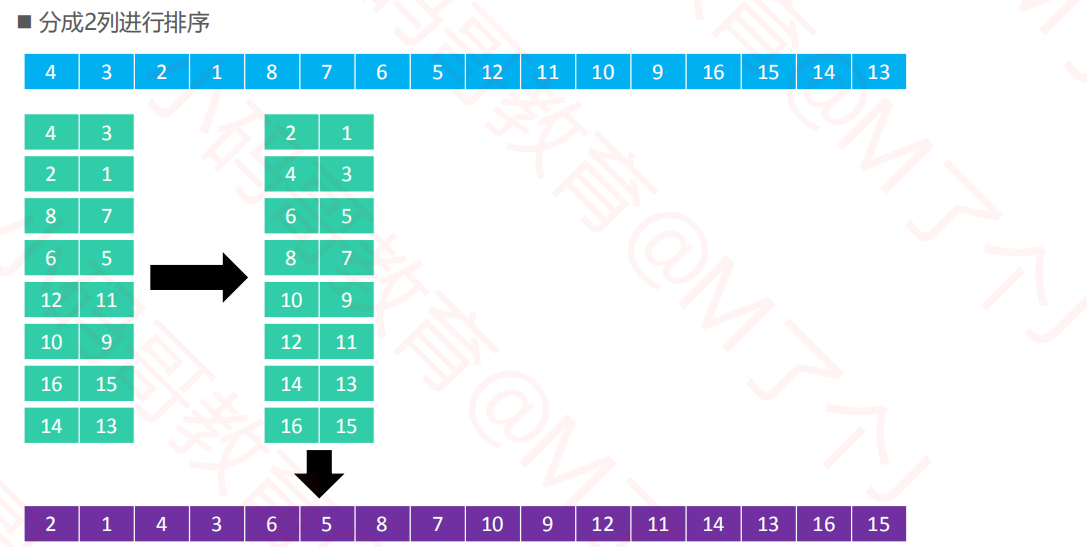
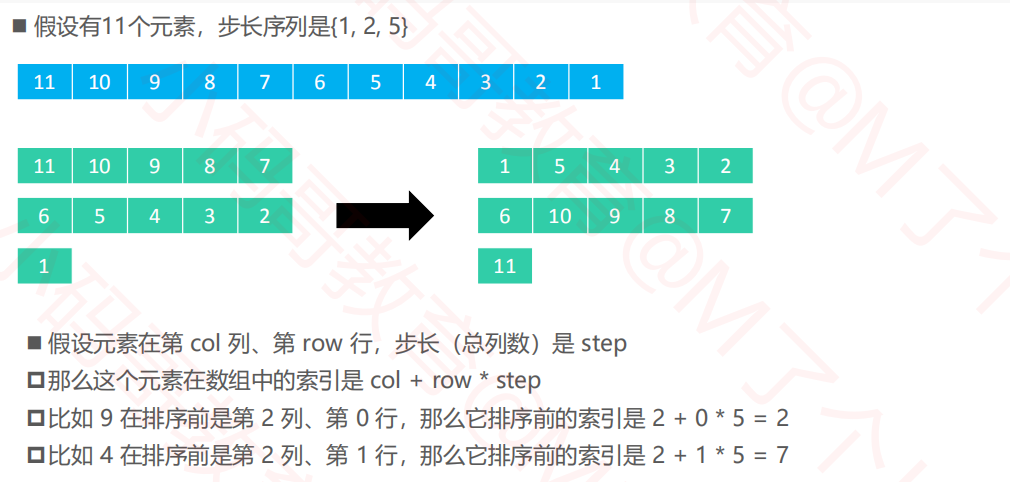
 2.3希尔排序--实现

 

 

 

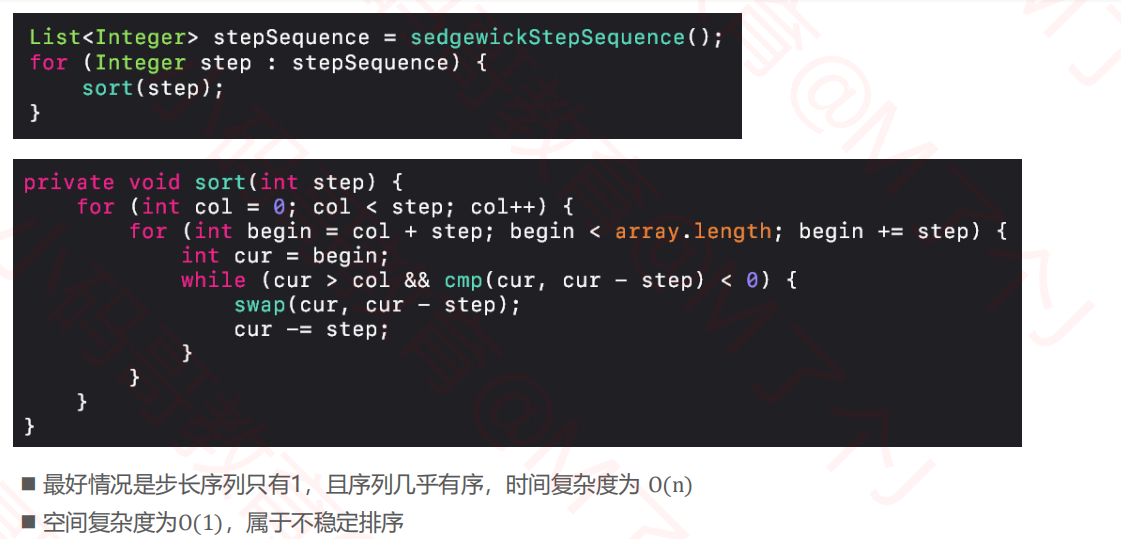
@Override
    protected void sort() {
        List<Integer> stepSequence = sedgewickStepSequence();
        for (Integer step : stepSequence) {
            sort(step);
        }
    }
    
    /**
     * 分成step列进行排序
     */
    private void sort(int step) {
        // col : 第几列，column的简称
        for (int col = 0; col < step; col++) { // 对第col列进行排序
            // col、col+step、col+2*step、col+3*step
            for (int begin = col + step; begin < array.length; begin += step) {
                int cur = begin;
                while (cur > col && cmp(cur, cur - step) < 0) {
                    swap(cur, cur - step);
                    cur -= step;
                }
            }
        }
    }
    
    private List<Integer> shellStepSequence() {
        List<Integer> stepSequence = new ArrayList<>();
        int step = array.length;
        while ((step >>= 1) > 0) {
            stepSequence.add(step);
        }
        return stepSequence;
    }

 

2.4希尔排序--步长实现

 

 

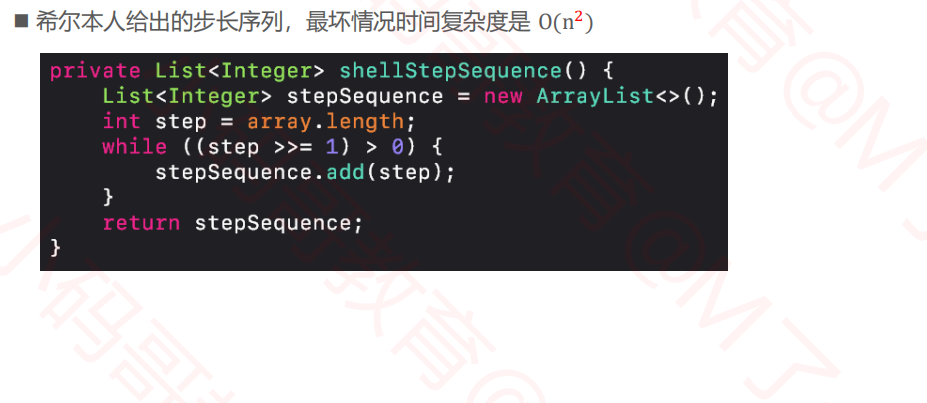
private List<Integer> shellStepSequence() {
        List<Integer> stepSequence = new ArrayList<>();
        int step = array.length;
        while ((step >>= 1) > 0) {
            stepSequence.add(step);
        }
        return stepSequence;
    }

 

 2.5希尔排序--步长优化

 

 

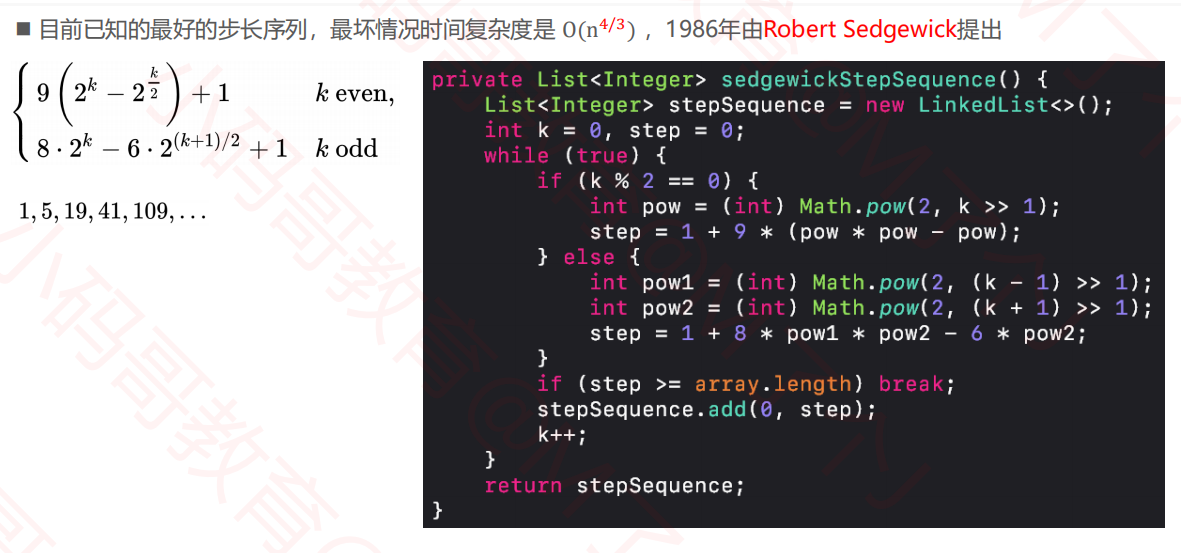
private List<Integer> sedgewickStepSequence() {
        List<Integer> stepSequence = new LinkedList<>();
        int k = 0, step = 0;
        while (true) {
            if (k % 2 == 0) {
                int pow = (int) Math.pow(2, k >> 1);
                step = 1 + 9 * (pow * pow - pow);
            } else {
                int pow1 = (int) Math.pow(2, (k - 1) >> 1);
                int pow2 = (int) Math.pow(2, (k + 1) >> 1);
                step = 1 + 8 * pow1 * pow2 - 6 * pow2;
            }
            if (step >= array.length) break;
            stepSequence.add(0, step);
            k++;
        }
        return stepSequence;
    }