排序03---[归并排序&&归并&&分离]

1.归并排序(Merge Sort)

1.1简介

 

 

 1.2归并排序--divide实现

 

 

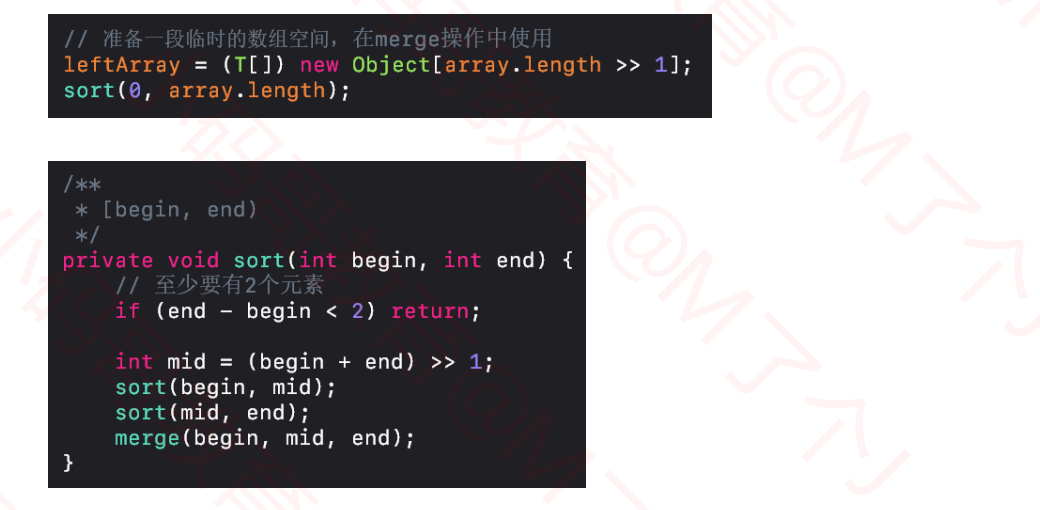
 1.3归并排序--merge

 

 

 

 1.4 归并排序--merge细节

 

 

 1.5归并排序--merge

 

 

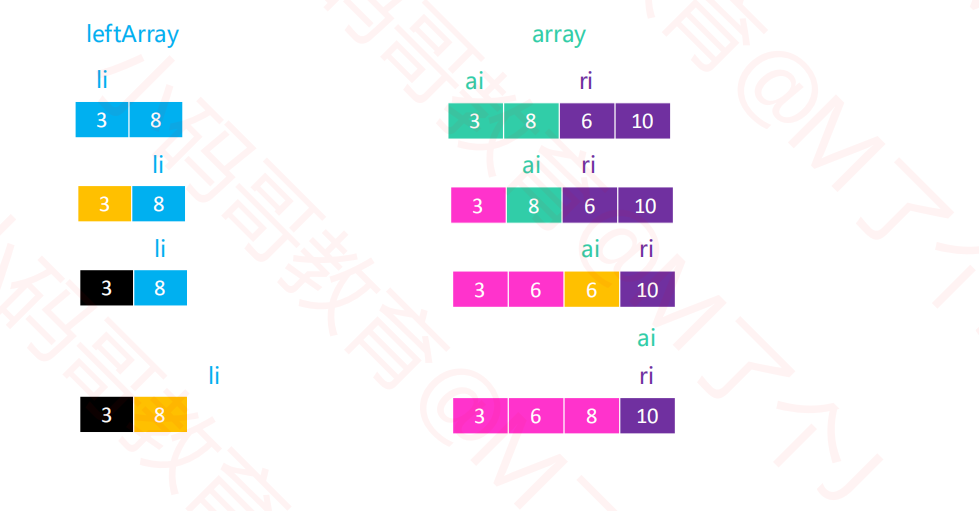
 1.6归并排序--merge--左边先结束

 

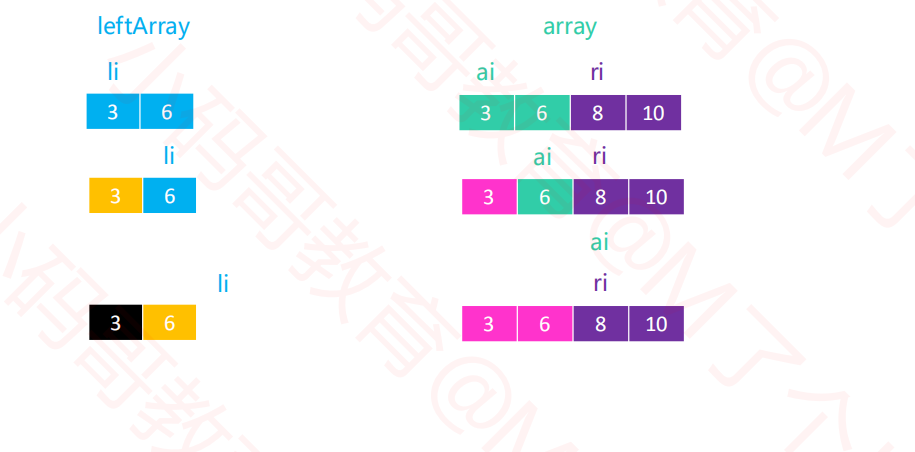
 1.7归并排序右边先结束

 

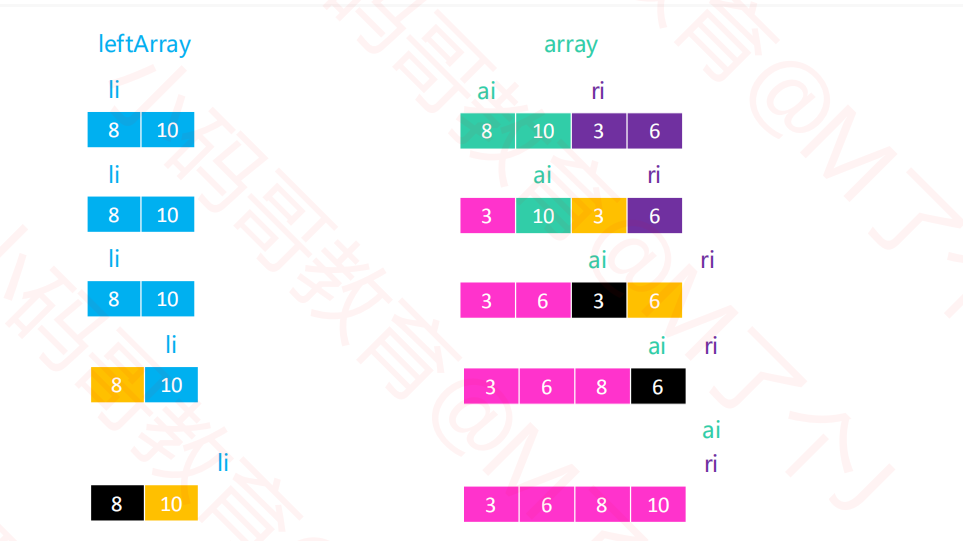
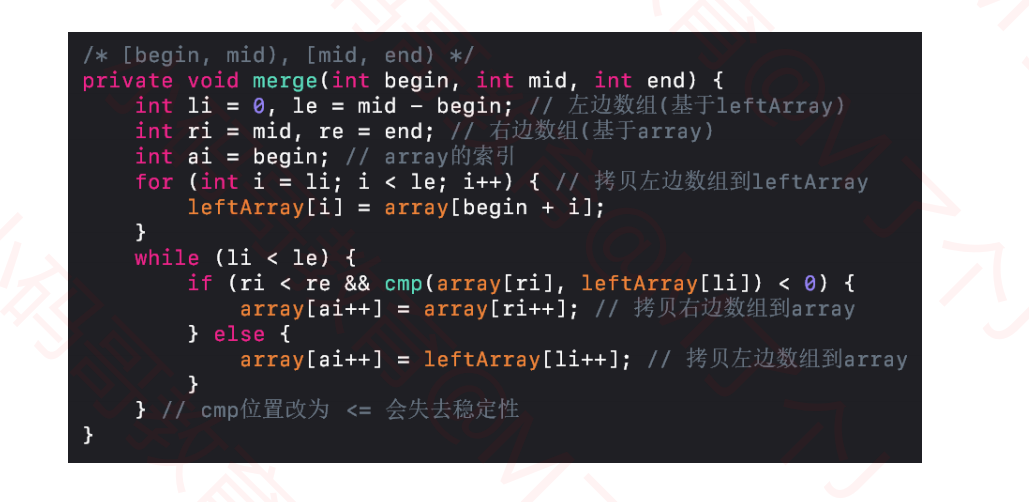
 1.8归并排序--merge实现

 

 1.9归并排序--复杂度分析

 

 1.10常见的递推式与复杂度

 

1.11代码

@Override
    protected void sort() {
        leftArray = (T[]) new Comparable[array.length >> 1];
        sort(0, array.length);
    }
    
    // T(n) = T(n/2) + T(n/2) + O(n)
    
    /**
     * 对 [begin, end) 范围的数据进行归并排序
     */
    private void sort(int begin, int end) {
        if (end - begin < 2) return;
        
        int mid = (begin + end) >> 1;
        sort(begin, mid);
        sort(mid, end);
        merge(begin, mid, end);
    }
    
    /**
     * 将 [begin, mid) 和 [mid, end) 范围的序列合并成一个有序序列
     */
    private void merge(int begin, int mid, int end) {
        int li = 0, le = mid - begin;
        int ri = mid, re = end;
        int ai = begin;
        
        // 备份左边数组
        for (int i = li; i < le; i++) {
            leftArray[i] = array[begin + i];
        }
        
        // 如果左边还没有结束
        while (li < le) { 
            if (ri < re && cmp(array[ri], leftArray[li]) < 0) {
                array[ai++] = array[ri++];
            } else {
                array[ai++] = leftArray[li++];
            }
        }
    }

 

1.12作业