排序02--[插入排序&&插入排序优化&&二分搜索]

1.插入排序(Insertion Sort)

1.基本介绍

 

 

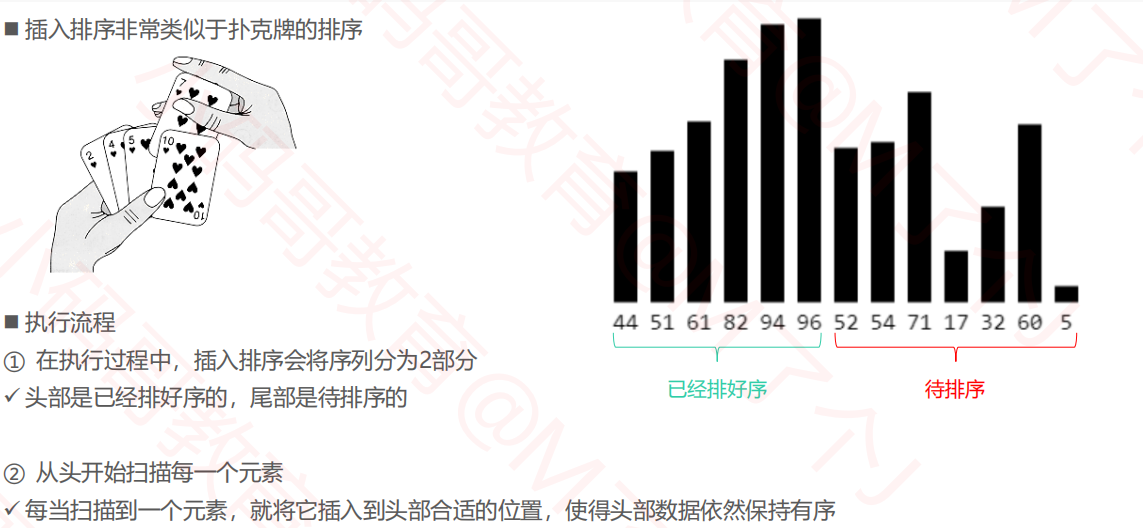
 1.2baseline算法实现

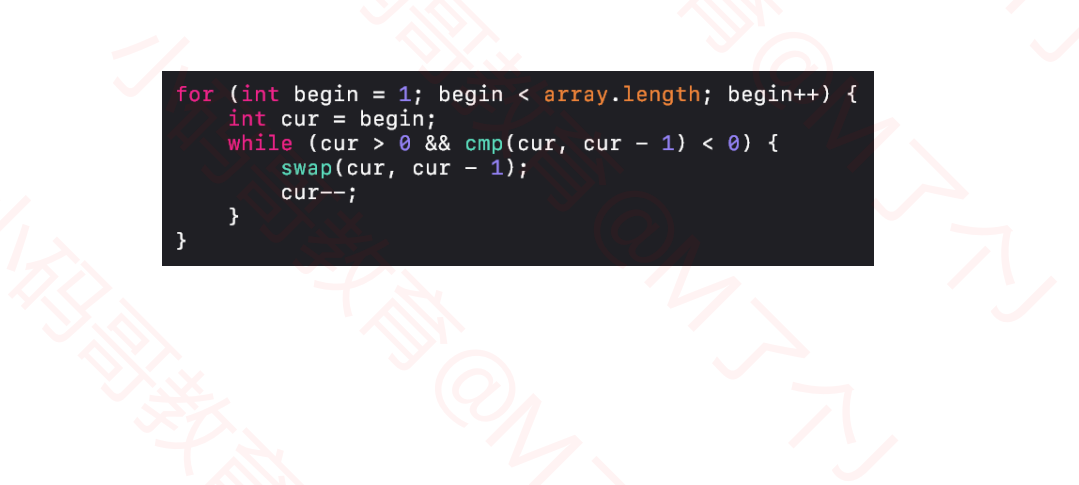
    @Override
    protected void sort() {
        for (int begin = 1; begin < array.length; begin++) {
            int cur = begin;
            while (cur > 0 && cmp(cur, cur - 1) < 0) {
                swap(cur, cur - 1);
                cur--;
            }
        }
    }

 

2.插入排序优化1--挪动

主要思路:

相对于baseline优化算法是 把交换的操作变成了挪动操作

2.1插入排序--逆序对(Inversion)

 

 

2.2插入排序优化

 

 

 

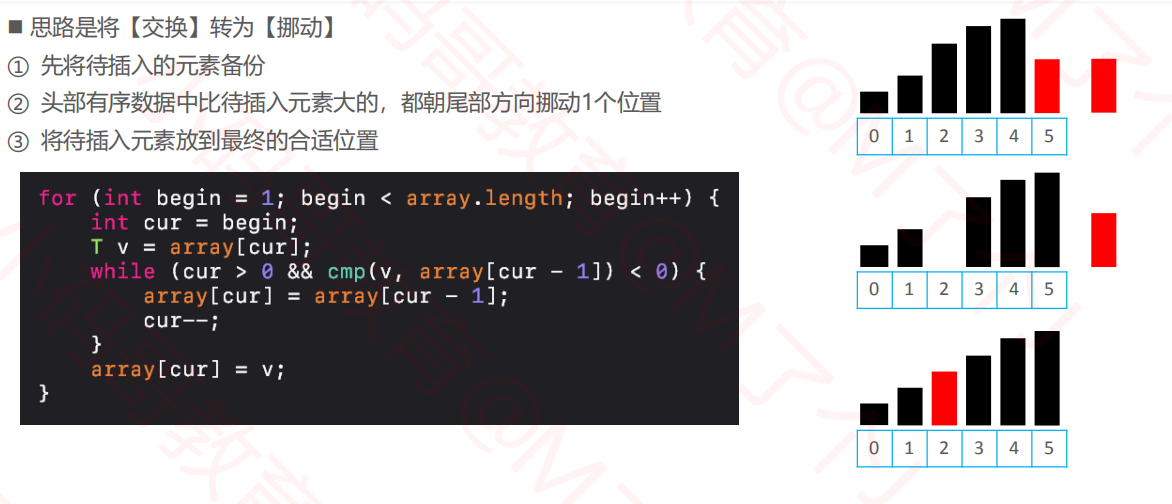
3.插入排序优化1--二分搜索

主要思路：

相对于优化1 主要将里面的搜索算法(遍历搜索算法)定位需要挪动的部分 通过二分搜索算法进行 定位 

3.1二分搜索

 

 

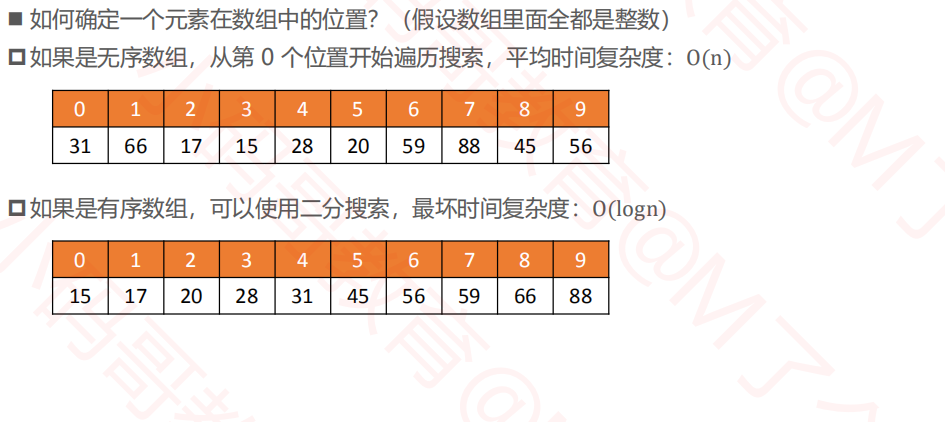
3.2二分搜索--思路

 

3.3二分搜索实例

 

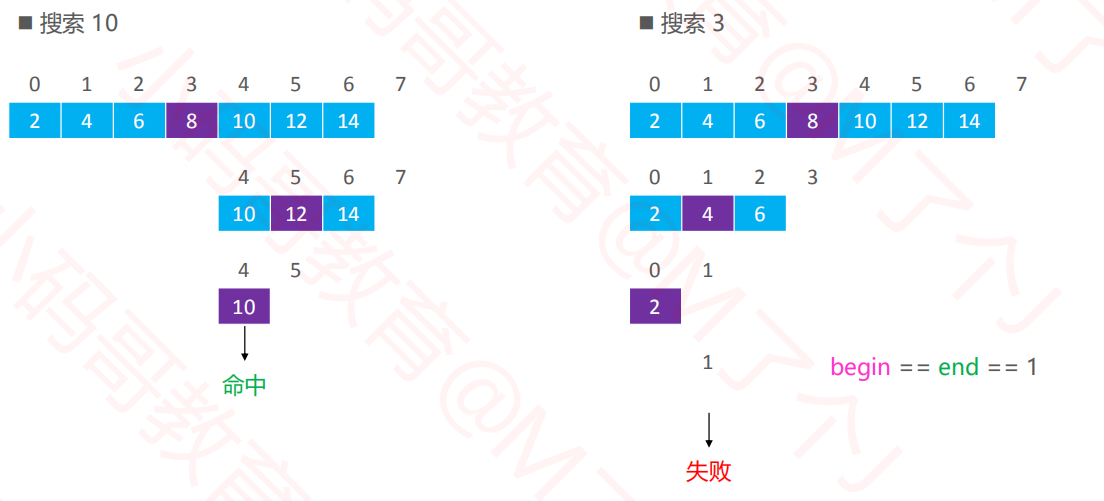
3.4二分搜索--实现

 

 

    /**
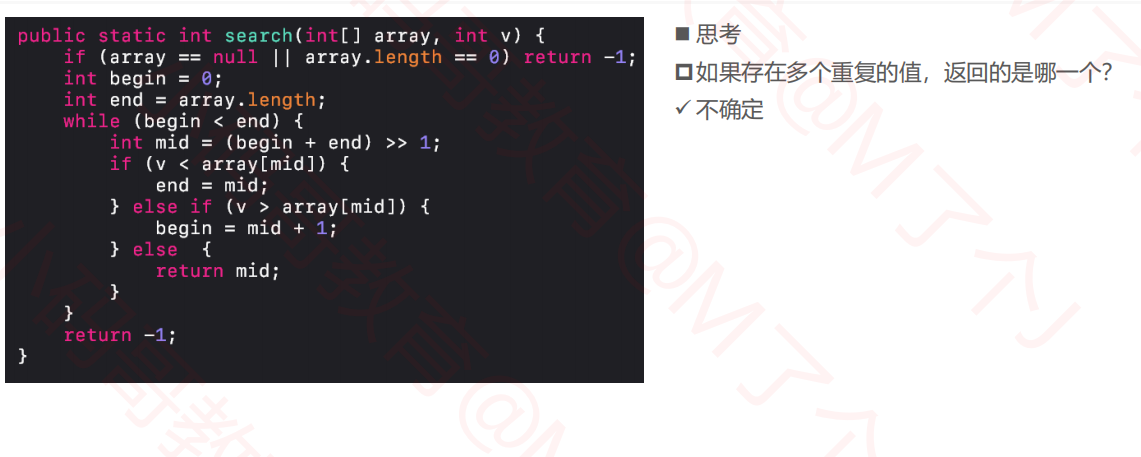
     * 查找v在有序数组array中待插入位置
     */
    public static int search(int[] array, int v) {
        if (array == null || array.length == 0) return -1;
        int begin = 0;
        int end = array.length;
        while (begin < end) {
            int mid = (begin + end) >> 1;
            if (v < array[mid]) {
                end = mid;
            } else {
                begin = mid + 1;
            }
        }
        return begin;
    }

 

3.5插入排序---二分搜索优化

 

3.6插入排序--二分搜索优化--思路

 

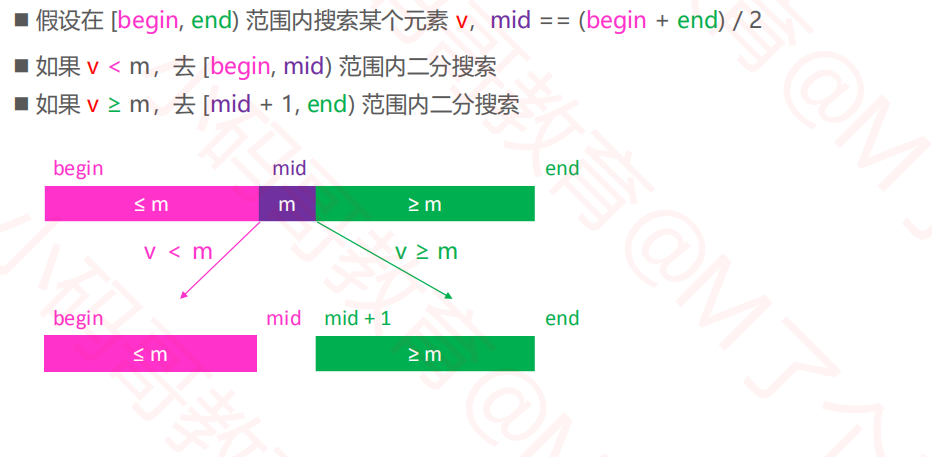
3.7插入排序-二分搜索优化--实例

 

3.8插入排序-二分搜索优化--实例2

 

 

3.9插入排序-二分搜索优化--实例3

 

3.10插入排序-二分搜索优化--实现

 

 

@Override
    protected void sort() {
        for (int begin = 1; begin < array.length; begin++) {
            insert(begin, search(begin));
        }
    }
    
    /**
     * 将source位置的元素插入到dest位置
     * @param source
     * @param dest
     */
    private void insert(int source, int dest) {
        T v = array[source];
        for (int i = source; i > dest; i--) {
            array[i] = array[i - 1];
        }
        array[dest] = v;
    }
    
    /**
     * 利用二分搜索找到 index 位置元素的待插入位置
     * 已经排好序数组的区间范围是 [0, index)
     * @param index
     * @return
     */
    private int search(int index) {
        int begin = 0;
        int end = index;
        while (begin < end) {
            int mid = (begin + end) >> 1;
            if (cmp(array[index], array[mid]) < 0) {
                end = mid;
            } else {
                begin = mid + 1;
            }
        }
        return begin;
    }