排序01---[排序基本知识&&冒泡排序&&选择排序&&堆排序]

1.排序基本知识

^{1.1初始排序}

 

 1.2十大排序算法

 

2.冒泡排序(Bubble Sort)

2.1Baseline

 

    static void bubbleSort1(Integer[] array) {
        for (int end = array.length - 1; end > 0; end--) {
            for (int begin = 1; begin <= end; begin++) {
                if (array[begin] < array[begin - 1]) {
                    int tmp = array[begin];
                    array[begin] = array[begin - 1];
                    array[begin - 1] = tmp;
                }
            }
        }
    }

2.2冒泡排序--优化1

 

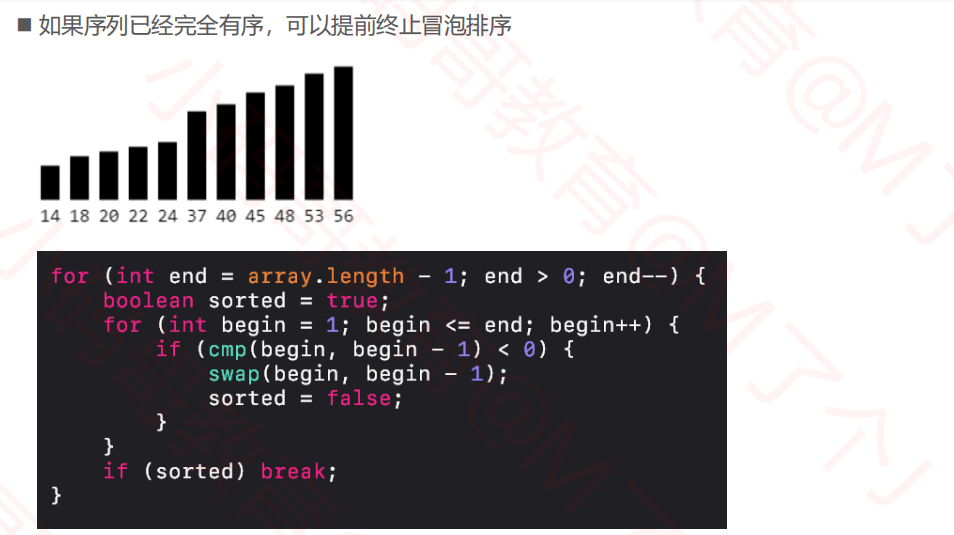
    static void bubbleSort2(Integer[] array) {
        for (int end = array.length - 1; end > 0; end--) {
            boolean sorted = true;
            for (int begin = 1; begin <= end; begin++) {
                if (array[begin] < array[begin - 1]) {
                    int tmp = array[begin];
                    array[begin] = array[begin - 1];
                    array[begin - 1] = tmp;
                    sorted = false;
                }
            }
            if (sorted) break;
        }
    }

2.3冒泡排序--优化2

 

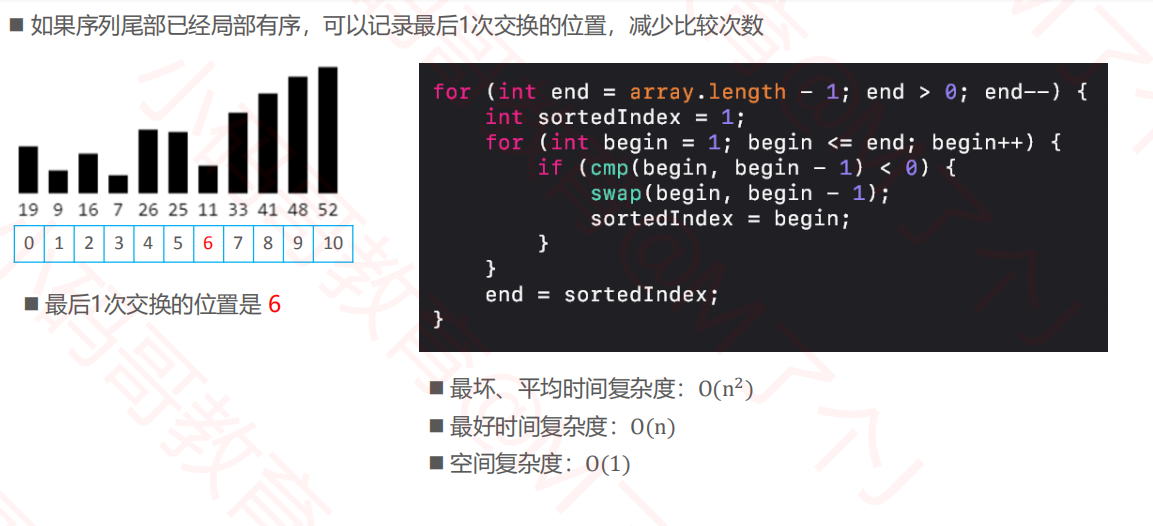
    static void bubbleSort3(Integer[] array) {
        for (int end = array.length - 1; end > 0; end--) {
            // sortedIndex的初始值在数组完全有序的时候有用
            int sortedIndex = 1;
            for (int begin = 1; begin <= end; begin++) {
                if (array[begin] < array[begin - 1]) {
                    int tmp = array[begin];
                    array[begin] = array[begin - 1];
                    array[begin - 1] = tmp;
                    sortedIndex = begin;
                }
            }
            end = sortedIndex;
        }
    }

2.4排序算法的稳定性(Stability)

 

 

 

 

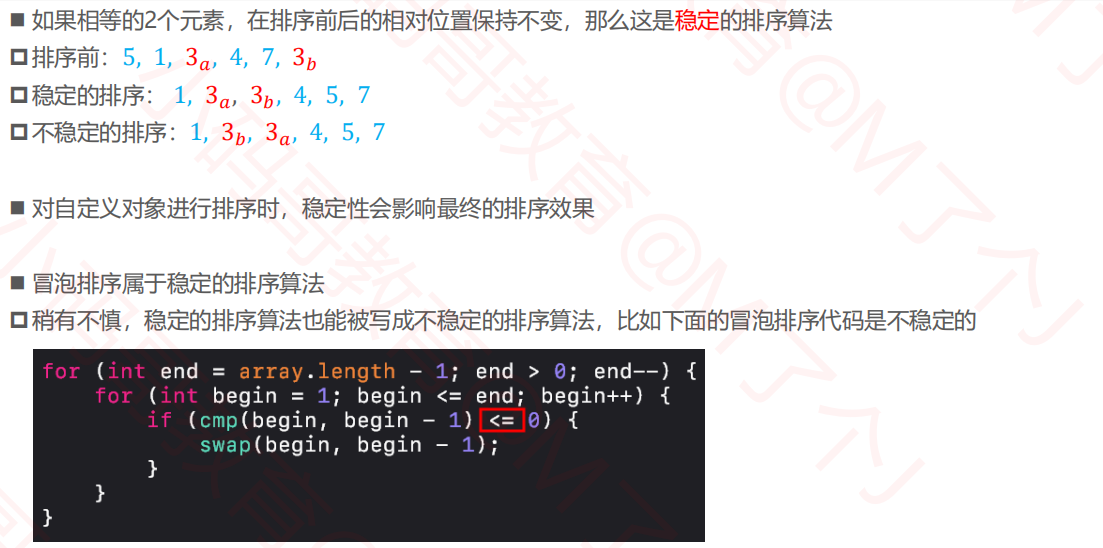
2.5原地算法(In-place Algorithm)

 

3.选择排序(Selection　Sort)

3.1Baseline

 

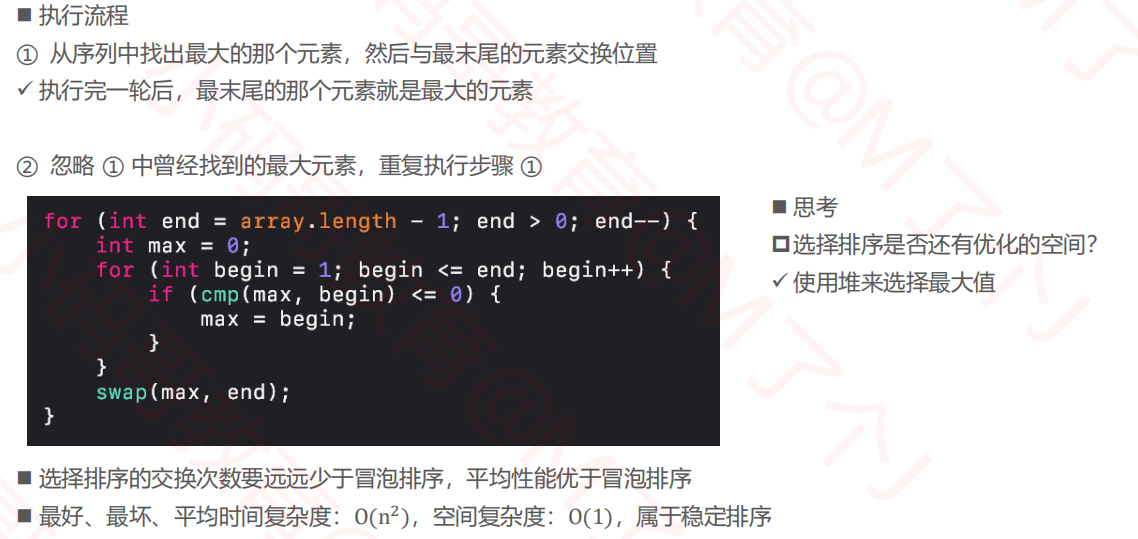
    static void selectionSort(Integer[] array) {
        for (int end = array.length - 1; end > 0; end--) {
            int maxIndex = 0;
            for (int begin = 1; begin <= end; begin++) {
                if (array[maxIndex] <= array[begin]) {
                    maxIndex = begin;
                }
            }
            int tmp = array[maxIndex];
            array[maxIndex] = array[end];
            array[end] = tmp;
        }
        
        // 8 10 9 10 
    }

 

 3.2堆排序(Heap Sort)

 

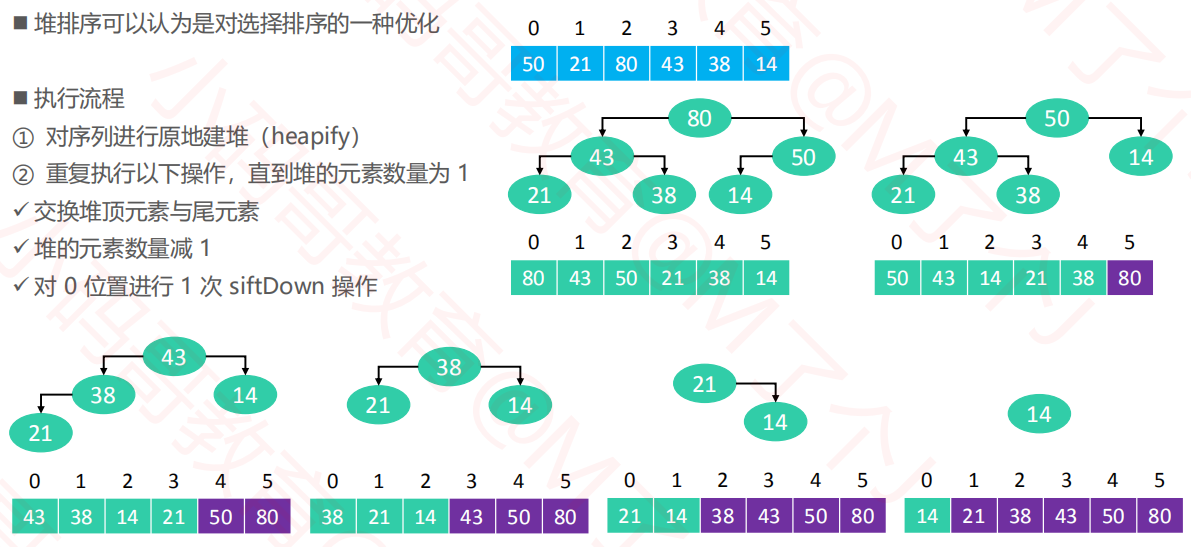
 3.3堆排序实现

package com.mj.sort.cmp;

import com.mj.sort.Sort;

public class HeapSort<T extends Comparable<T>> extends Sort<T> {
    private int heapSize;

    @Override
    protected void sort() {
        // 原地建堆
        heapSize = array.length;
        for (int i = (heapSize >> 1) - 1; i >= 0; i--) {
            siftDown(i);
        }
        
        while (heapSize > 1) {
            // 交换堆顶元素和尾部元素
            swap(0, --heapSize);

            // 对0位置进行siftDown（恢复堆的性质）
            siftDown(0);
        }
    }
    
    private void siftDown(int index) {
        T element = array[index];
        
        int half = heapSize >> 1;
        while (index < half) { // index必须是非叶子节点
            // 默认是左边跟父节点比
            int childIndex = (index << 1) + 1;
            T child = array[childIndex];
            
            int rightIndex = childIndex + 1;
            // 右子节点比左子节点大
            if (rightIndex < heapSize && 
                    cmp(array[rightIndex], child) > 0) { 
                child = array[childIndex = rightIndex];
            }
            
            // 大于等于子节点
            if (cmp(element, child) >= 0) break;
            
            array[index] = child;
            index = childIndex;
        }
        array[index] = element;
    }
}