数据结构与算法01--[复杂度]

1.什么是算法

算法是解决特定问题的一系列步骤

使用不同算法解决同意问题的效率可能相差很大

2.如何评价一个算法好坏

2.1事后统计法

2.2常用分析指标

正确性可读性　健壮性

时间复杂度

空间复杂度

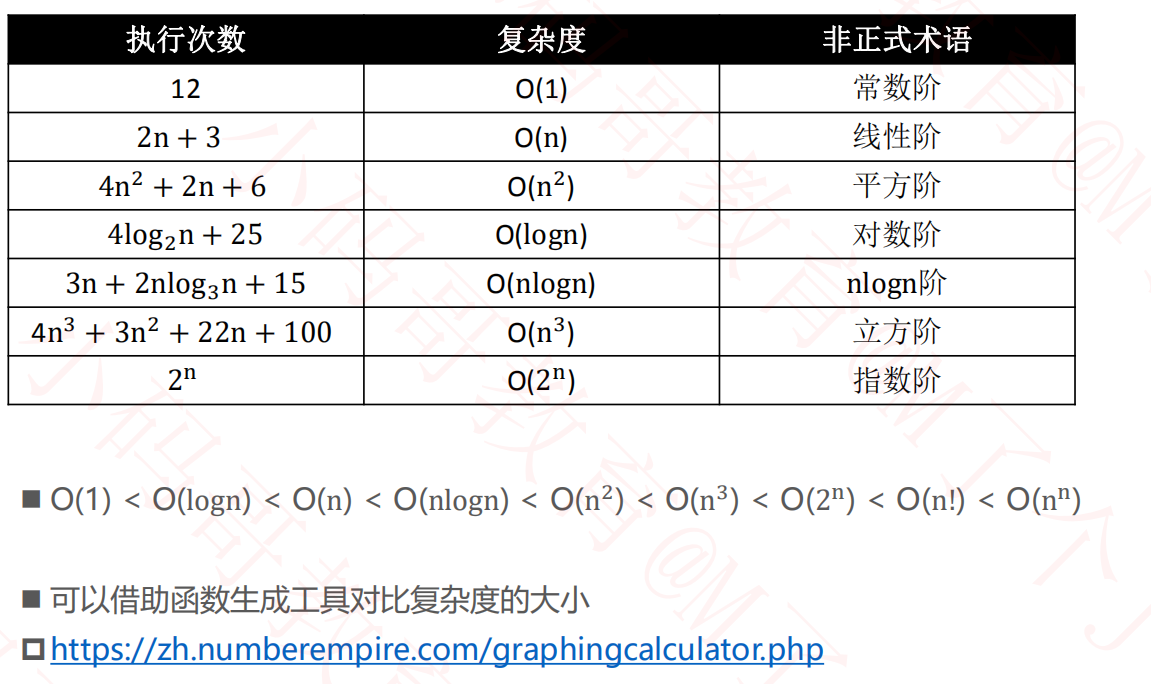
3.大O表示法

3.1对数阶的细节

3.2常见的复杂度

4.常见一些函数的复杂度表示

public static void test2(int n) {
        // O(n)
        // 1 + 3n
        for (int i = 0; i < n; i++) {
            System.out.println("test");
        }
    }

    public static void test3(int n) {
        // 1 + 2n + n * (1 + 3n)
        // 1 + 2n + n + 3n^2
        // 3n^2 + 3n + 1
        // O(n^2)
        
        // O(n)
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.println("test");
            }
        }
    }

    public static void test4(int n) {
        // 1 + 2n + n * (1 + 45)
        // 1 + 2n + 46n
        // 48n + 1
        // O(n)
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < 15; j++) {
                System.out.println("test");
            }
        }
    }

    public static void test5(int n) {
        // 8 = 2^3
        // 16 = 2^4
        
        // 3 = log2(8)
        // 4 = log2(16)
        
        // 执行次数 = log2(n)
        // O(logn)
        while ((n = n / 2) > 0) {
            System.out.println("test");
        }
    }

    public static void test6(int n) {
        // log5(n)
        // O(logn)
        while ((n = n / 5) > 0) {
            System.out.println("test");
        }
    }

    public static void test7(int n) {
        // 1 + 2*log2(n) + log2(n) * (1 + 3n)
        
        // 1 + 3*log2(n) + 2 * nlog2(n)
        // O(nlogn)
        for (int i = 1; i < n; i = i * 2) {
            // 1 + 3n
            for (int j = 0; j < n; j++) {
                System.out.println("test");
            }
        }
    }

    public static void test10(int n) {
        // O(n)
        int a = 10;
        int b = 20;
        int c = a + b;
        int[] array = new int[n];
        for (int i = 0; i < array.length; i++) {
            System.out.println(array[i] + c);
        }
    }

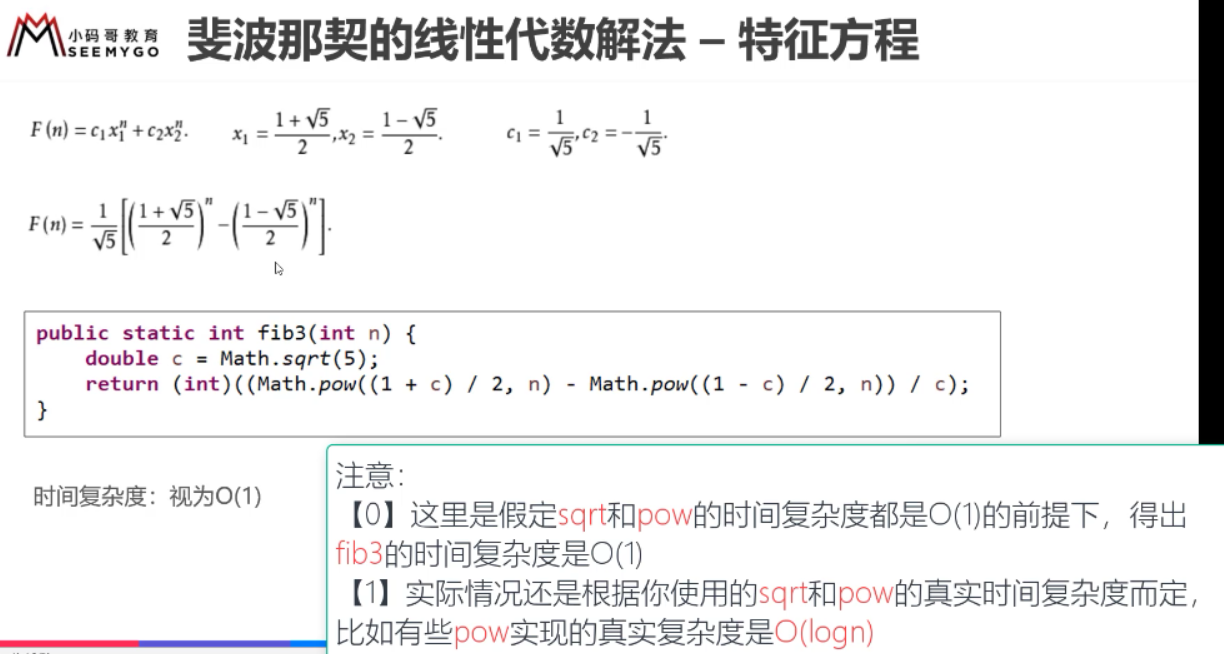
4.1斐波拉切数

/* 0 1 2 3 4 5
     * 0 1 1 2 3 5 8 13 ....
     */
    
    // O(2^n)
    public static int fib1(int n) {
        if (n <= 1) return n;
        return fib1(n - 1) + fib1(n - 2);
    }
    
    // O(n)
    public static int fib2(int n) {
        if (n <= 1) return n;
        
        int first = 0;
         
        int second = 1;
        for (int i = 0; i < n - 1; i++) {
            int sum = first + second;
            first = second;
            second = sum;
        }
        return second;
    }
    
    public static int fib3(int n) {
        if (n <= 1) return n;
        
        int first = 0;
        int second = 1;
        while (n-- > 1) {
            second += first;
            first = second - first;
        }
        return second;
    }