软件姿态解算
使用MPU6050硬件DMP解算姿态是非常简单的,下面介绍由三轴陀螺仪和加速度计的值来使用四元数软件解算姿态的方法。
我们先来看看如何用欧拉角描述一次平面旋转(坐标变换):

设坐标系绕旋转α角后得到坐标系,在空间中有一个矢量在坐标系中的投影为,在内的投影为由于旋转绕进行,所以Z坐标未变,即有。
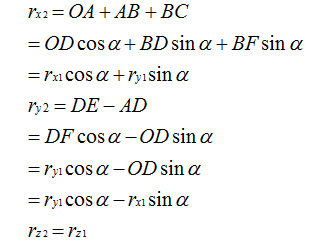
转换成矩阵形式表示为:

整理一下:

所以从旋转到可以写成
上面仅仅是绕一根轴的旋转,如果三维空间中的欧拉角旋转要转三次:

上面得到了一个表示旋转的方向余弦矩阵。
不过要想用欧拉角解算姿态,其实我们套用欧拉角微分方程就行了:
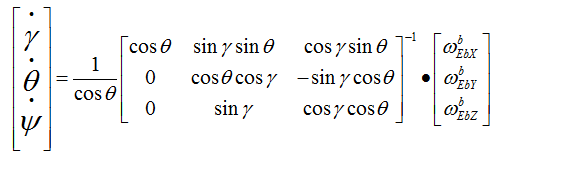
上式中左侧,,是本次更新后的欧拉角,对应row,pit,yaw。右侧,是上个周期测算出来的角度,,,三个角速度由直接安装在四轴飞行器的三轴陀螺仪在这个周期转动的角度,单位为弧度,计算间隔时T陀螺角速度,比如0.02秒0.01弧度/秒=0.0002弧度。间因此求解这个微分方程就能解算出当前的欧拉角。
前面介绍了什么是欧拉角,而且欧拉角微分方程解算姿态关系简单明了,概念直观容易理解,那么我们为什么不用欧拉角来表示旋转而要引入四元数呢?
一方面是因为欧拉角微分方程中包含了大量的三角运算,这给实时解算带来了一定的困难。而且当俯仰角为90度时方程式会出现神奇的“GimbalLock”。所以欧拉角方法只适用于水平姿态变化不大的情况,而不适用于全姿态飞行器的姿态确定。
四元数法只求解四个未知量的线性微分方程组,计算量小,易于操作,是比较实用的工程方法。
我们知道在平面(x,y)中的旋转可以用复数来表示,同样的三维中的旋转可以用单位四元数来描述。我们来定义一个四元数:
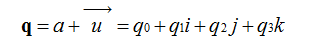
或写为Q(w,x,y,z)其中x,y,z是矢量,表示三维空间中的旋转轴。w是标量,表示旋转角度。那么就是绕轴旋转w度,所以一个四元数可以表示一个完整的旋转。只有单位四元数才可以表示旋转,至于为什么,因为这就是四元数表示旋转的约束条件。
而刚才用欧拉角描述的方向余弦矩阵用四元数描述则为:
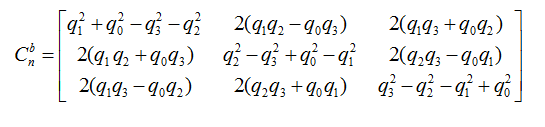
所以在软件解算中,我们要首先把加速度计采集到的值(三维向量)转化为单位向量,即向量除以模,传入参数是陀螺仪x,y,z值和加速度计x,y,z值:
1 void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az) { 2 float norm; 3 float vx, vy, vz; 4 float ex, ey, ez; 5 6 norm = sqrt(ax*ax + ay*ay + az*az); 7 ax = ax / norm; 8 ay = ay / norm; 9 az = az / norm;
下面把四元数换算成方向余弦中的第三行的三个元素。刚好vx,vy,vz 其实就是上一次的欧拉角(四元数)的机体坐标参考系换算出来的重力的单位向量。
1 // estimated direction of gravity 2 vx = 2*(q1*q3 - q0*q2); 3 vy = 2*(q0*q1 + q2*q3); 4 vz = q0*q0 - q1*q1 - q2*q2 + q3*q3;
axyz是机体坐标参照系上,加速度计测出来的重力向量,也就是实际测出来的重力向量。
axyz是测量得到的重力向量,vxyz是陀螺积分后的姿态来推算出的重力向量,它们都是机体坐标参照系上的重力向量。
那它们之间的误差向量,就是陀螺积分后的姿态和加计测出来的姿态之间的误差。
向量间的误差,可以用向量叉积(也叫向量外积、叉乘)来表示,exyz就是两个重力向量的叉积。
这个叉积向量仍旧是位于机体坐标系上的,而陀螺积分误差也是在机体坐标系,而且叉积的大小与陀螺积分误差成正比,正好拿来纠正陀螺。(你可以自己拿东西想象一下)由于陀螺是对机体直接积分,所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。
1 // integral error scaled integral gain 2 exInt = exInt + ex*Ki; 3 eyInt = eyInt + ey*Ki; 4 ezInt = ezInt + ez*Ki;
用叉积误差来做PI修正陀螺零偏
1 // integral error scaled integral gain 2 exInt = exInt + ex*Ki; 3 eyInt = eyInt + ey*Ki; 4 ezInt = ezInt + ez*Ki; 5 6 // adjusted gyroscope measurements 7 gx = gx + Kp*ex + exInt; 8 gy = gy + Kp*ey + eyInt; 9 gz = gz + Kp*ez + ezInt;
四元数微分方程,其中T为测量周期,为陀螺仪角速度,以下都是已知量,这里使用了一阶龙哥库塔求解四元数微分方程:

1 // integrate quaternion rate and normalise 2 q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT; 3 q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT; 4 q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT; 5 q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
最后根据四元数方向余弦阵和欧拉角的转换关系,把四元数转换成欧拉角:

所以有:
1 Q_ANGLE.Yaw = atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3* q3 + 1)* 57.3; // yaw 2 Q_ANGLE.Y = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch 3 Q_ANGLE.X = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // roll




