leetcode-215. 数组中的第K个最大元素

快速选择

---

题目详情

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。
请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

---

示例1：

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

我的方法：

1.快速选择

快速选择一般用于求解 k-th Element 问题，可以在 O(n) 时间复杂度，O(1) 空间复杂度完成求解工作。快速选择的实现和快速排序相似，不过只需要找到第 k 大的枢（pivot）即可，不需要对其左右再进行排序。与快速排序一样，快速选择一般需要先打乱数组，否则最坏情况下时间复杂度为 O(n2)

省略掉打乱的代码:

class Solution
{
public:
    int findKthLargest(vector<int>& nums, int k)
    {
        int l = 0, r = nums.size() - 1, target = nums.size() - k; //第k大即第target小
        while (l < r) {
            int mid = quickSelection(nums, l, r);
            if (mid == target)                                    //找到
            {
                return nums[mid];
            }
            if (mid < target)                                   //偏小,则在右区间[mid+1,r]继续寻找
            {
                l = mid + 1;
            }
            else                                                //偏大,则在左区间[l,mid-1]继续寻找
            {
                r = mid - 1;
            }
        }
        return nums[l];                                         //返回找到的值

    }
    //基于快速排序的快速选择函数
    int quickSelection(vector<int>& nums, int l, int r) 
    {
        int i = l + 1, j = r;
        while (true) 
        {
            while (i < r && nums[i] <= nums[l]) //i从左往右寻找大于nums[l]的并停止
            {
                ++i;
            }
            while (l < j && nums[j] >= nums[l]) //j从右往左寻找小于nums[l]的并停止
            {
                --j;
            }
           if(i>=j)                             //如果都找到后,但是i和j相遇或擦肩而过了
            {                                   //则此时不满足交换条件,说明l处值已经是他自己的位置了
              break;                            //直接break
            }
              swap(nums[i], nums[j]);           //如果没有break,就像快速排序一样一直交换大小值
        }
        swap(nums[l], nums[j]);                 //l归位
        return j;                                //返回的是这次快排归位的那个数的下标
    }
};

效率:

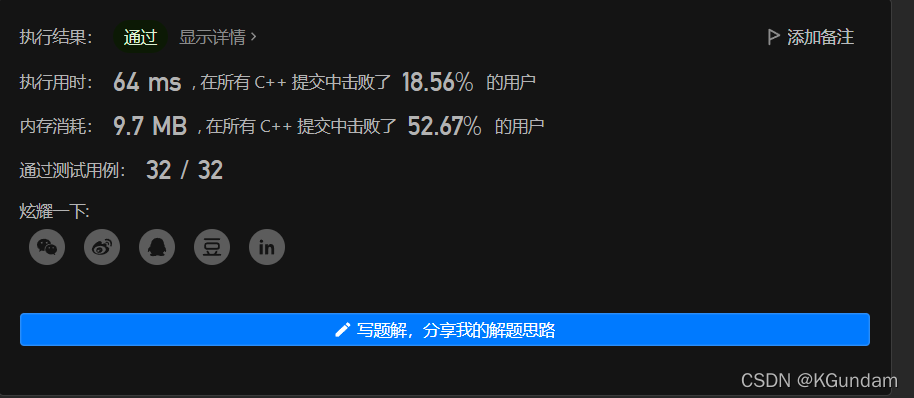
加上打乱语句random_shuffle ( nums.begin(), nums.end() );后:

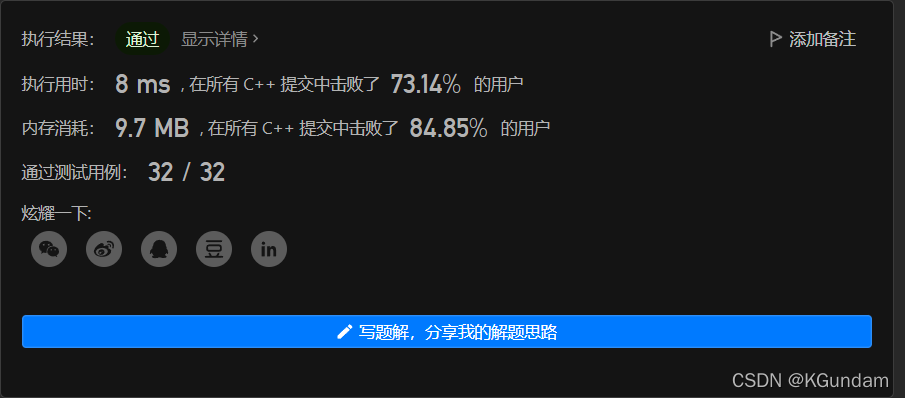
明显提高了时间和内存
最终代码:

class Solution
{
public:
    int findKthLargest(vector<int>& nums, int k)
    {
        random_shuffle ( nums.begin(), nums.end() );
        int l = 0, r = nums.size() - 1, target = nums.size() - k; //第k大即第target小
        while (l < r) {
            int mid = quickSelection(nums, l, r);
            if (mid == target)                                    //找到
            {
                return nums[mid];
            }
            if (mid < target)                                   //偏小,则在右区间[mid+1,r]继续寻找
            {
                l = mid + 1;
            }
            else                                                //偏大,则在左区间[l,mid-1]继续寻找
            {
                r = mid - 1;
            }
        }
        return nums[l];                                         //返回找到的值

    }
    //基于快速排序的快速选择函数
    int quickSelection(vector<int>& nums, int l, int r) 
    {
        int i = l + 1, j = r;
        while (true) 
        {
            while (i < r && nums[i] <= nums[l]) //i从左往右寻找大于nums[l]的并停止
            {
                ++i;
            }
            while (l < j && nums[j] >= nums[l]) //j从右往左寻找小于nums[l]的并停止
            {
                --j;
            }
           if(i>=j)                             //如果都找到后,但是i和j相遇或擦肩而过了
            {                                   //则此时不满足交换条件,说明l处值已经是他自己的位置了
              break;                            //直接break
            }
              swap(nums[i], nums[j]);           //如果没有break,就像快速排序一样一直交换大小值
        }
        swap(nums[l], nums[j]);                 //l归位
        return j;                                //返回的是这次快排归位的那个数的下标
    }
};