leetcode-695. 岛屿的最大面积
深度优先搜索(dfs)
题目详情
给你一个大小为m x n的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。
示例1：
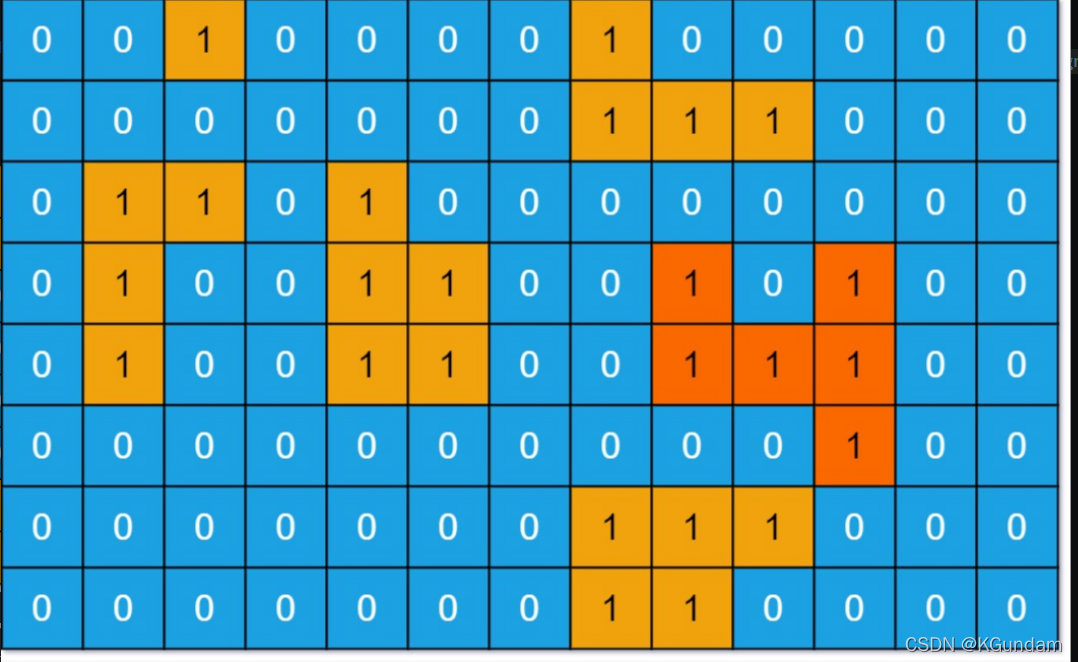
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例2:
输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0
第一种代码(栈)：
class Solution
{
public:
vector<int> direction{-1, 0, 1, 0, -1}; //利用direction来控制方向搜索
int maxAreaOfIsland(vector<vector<int>>& grid)
{
//m为行 n为列 临时块 最大块
int m = grid.size(), n = m? grid[0].size() : 0,local_area, area = 0, x, y;
for (int i = 0;i < m; ++i)
{
for (int j =0;j < n; ++j)
{
if(grid[i][j]) //遍历到的是陆地
{
local_area = 1; //临时增加一块陆地
grid[i][j] = 0; //遍历过的块归零
stack<pair<int, int>> island; //用存pair数据的栈存陆地点
island.push({i, j}); //将这块陆地点入栈
while (!island.empty())
{
auto [r, c] = island.top(); //[r,c]数对暂存栈顶元素
island.pop(); //栈顶元素无用了出栈
for (int k = 0; k < 4; ++k)
{
x = r + direction[k], y = c + direction[k+1]; //开始上下左右移动搜寻
//x = r + -1 , y = c + 0 ----行-1,即向上
//x = r + 0 , y = c + 1 ----列+1,即向右
//x = r + 1 , y = c + 0 ----行+1,即向下
//x = r + 0 , y = c + -1 ----列-1,即向左
//确保不越界 且 该块为陆地
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1)
{
grid[x][y] = 0; //遍历过的块归零
++local_area; //此次while扩容的总面积+1
island.push({x, y}); //将新块入栈
}
}
}
area = max(area, local_area); //每一次while就比较是否更新一次最大面积
}
}
}
return area;
}
};
第二种方法(递归)(辅函数先判定是否越界，只有在合法的情况下才进行下一步搜索（即判断放在调用递归函数前))
class Solution
{
public:
vector<int> direction{-1, 0, 1, 0, -1}; //利用direction来控制方向搜索
//辅函数,用来递归移动搜索
int dfs(vector<vector<int>>& grid, int r, int c)
{
if (grid[r][c] == 0) //海水返回0,同时这里也是递归出口
return 0;
grid[r][c] = 0; //搜索过的陆地归零为海水
int x, y, area = 1; //area总面积初始化为1
for (int i = 0; i < 4; ++i)
{
//上下左右遍历
x = r + direction[i], y = c + direction[i+1];
if (x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size()) //不越界
{
area += dfs(grid, x, y); //递归继续寻找,加上相应的面积
}
}
return area;
}
int maxAreaOfIsland(vector<vector<int>>& grid)
{
if (grid.empty() || grid[0].empty()) //空的直接返回0
return 0;
int max_area = 0; //存最大面积
//遍历寻找陆地并更新max_area
for (int i = 0; i < grid.size(); ++i)
{
for (int j = 0;j < grid[0].size(); ++j)
{
if(grid[i][j] == 1)
{
max_area = max(max_area, dfs(grid, i, j));
}
}
}
return max_area;
}
};
另一种递归(不管三七二十一先进行下一步搜索，待下一步搜索开始时再判断是否合法（即判断放在辅函数第一行）)
//上一种递归是判断好下一块不越界再dfs下一块
//这一种递归是dfs下一块之后再在下一块判断是否越界
class Solution
{
public:
//辅函数,用来递归四面八方搜索
int dfs(vector<vector<int>>& grid, int r, int c)
{
//越界或为海水
if (r < 0 || r >= grid.size() || c < 0 || c >= grid[0].size() || grid[r][c] == 0)
return 0;
grid[r][c] = 0;
return 1 + dfs(grid, r + 1, c) + dfs(grid, r - 1, c) + dfs(grid, r, c + 1) + dfs(grid, r, c-1);
}
int maxAreaOfIsland(vector<vector<int>>& grid)
{
if(grid.empty() || grid[0].empty())
return 0;
int max_area = 0;
for (int i = 0; i < grid.size(); ++i)
{
for (int j = 0; j < grid[0].size(); ++j)
{
max_area = max(max_area, dfs(grid, i, j));
}
}
return max_area;
}
};
涉及知识点:
1.深度优先搜索(dfs)
深度优先搜索（depth-first seach，DFS）在搜索到一个新的节点时，立即对该新节点进行遍历；因此遍历需要用先入后出的栈来实现，也可以通过与栈等价的递归来实现。对于树结构而言，由于总是对新节点调用遍历，因此看起来是向着“深”的方向前进。
