leetcode-417.太平洋大西洋水流问题
深度优先搜索(dfs)
题目详情
有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。
岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回 网格坐标 result 的 2D列表 ,其中result[i] = [ri, ci]表示雨水可以从单元格(ri, ci)流向 太平洋和大西洋 。
示例1:
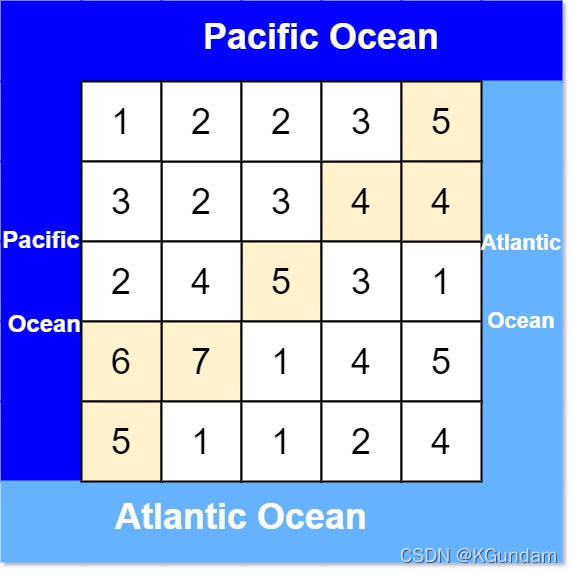
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例2:
输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]
我的代码:
思路:
题目要求的是满足向下流能到达两个大洋的位置,如果我们对所有的位置进行搜索,那么复杂度会很高。因此我们可以反过来想,从两个大洋开始向上流,这样我们只需要对矩形四条边进行搜索。搜索完成后,只需遍历一遍矩阵,满足条件的位置即为两个大洋向上流都能到达的位置。
详细:
class Solution
{
public:
vector<int> direction{-1, 0, 1, 0, -1};
void dfs(const vector<vector<int>>& heights, vector<vector<bool>>& can_reach, int r, int c)
{
if (can_reach[r][c]) //能反流到,则退出这次dfs
return;
can_reach[r][c] = true; //反流不到,置为能反流到防止下次遍历
int x, y;
for (int i = 0;i < 4; ++i) //从[r,c]向四个方向遍历
{
x = r + direction[i], y = c + direction[i+1];
//不越界 且 海水倒流不到的板块 继续dfs(海水倒流不到,所以肯定能流进海水)
if (x >= 0 && x < heights.size() && y >= 0 && y < heights[0].size() && heights[r][c] <= heights[x][y])
{
dfs(heights, can_reach, x, y);
}
}
}
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights)
{
if (heights.empty() || heights[0].empty())
return {};
vector<vector<int>> ans;
int m = heights.size(), n = heights[0].size();
vector<vector<bool>> can_reach_p(m, vector<bool>(n, false)); //太平洋
vector<vector<bool>> can_reach_a(m, vector<bool>(n, false)); //大西洋
//矩阵四条边往里流水
//左右两条边
for (int i = 0;i < m; ++i)
{
dfs(heights, can_reach_p, i, 0); //[0,0] [1,0] [2,0]...--左边(太平洋逆流验证)
dfs(heights, can_reach_a, i, n-1); //[0,n-1] [1,n-1].....--右边(大西洋逆流验证)
}
//上下两条边
for (int i = 0; i < n; ++i)
{
dfs(heights, can_reach_p, 0, i); //[0,0] [0,1] [0,2]...--上边(太平洋逆流验证)
dfs(heights, can_reach_a, m-1, i); //[m-1,0] [m-1,1] ....--下边(大西洋逆流验证)
}
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < n; ++j)
{
if(can_reach_a[i][j] && can_reach_p[i][j]) //都不能倒流到,所以都能流出
ans.push_back(vector<int>{i, j});
}
}
return ans;
}
};
涉及知识点:
1.深度优先搜索(dfs)
深度优先搜索(depth-first seach,DFS)在搜索到一个新的节点时,立即对该新节点进行遍历;因此遍历需要用先入后出的栈来实现,也可以通过与栈等价的递归来实现。对于树结构而言,由于总是对新节点调用遍历,因此看起来是向着“深”的方向前进。




