leetcode-241.为运算表达式设计优先级
分治法(递归实现)
题目详情
给你一个由数字和运算符组成的字符串 expression ，按不同优先级组合数字和运算符，计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
生成的测试用例满足其对应输出值符合 32 位整数范围，不同结果的数量不超过 104 。
示例1：
输入：expression = "2-1-1"
输出：[0,2]
解释：
((2-1)-1) = 0
(2-(1-1)) = 2
示例2:
输入：expression = "2*3-4*5"
输出：[-34,-14,-10,-10,10]
解释：
(2*(3-(4*5))) = -34
((2*3)-(4*5)) = -14
((2*(3-4))*5) = -10
(2*((3-4)*5)) = -10
(((2*3)-4)*5) = 10
思路:对于每个运算符号，先执行处理两侧的数学表达式，再处理此运算符号。
这里引用一张力扣题解的图片:
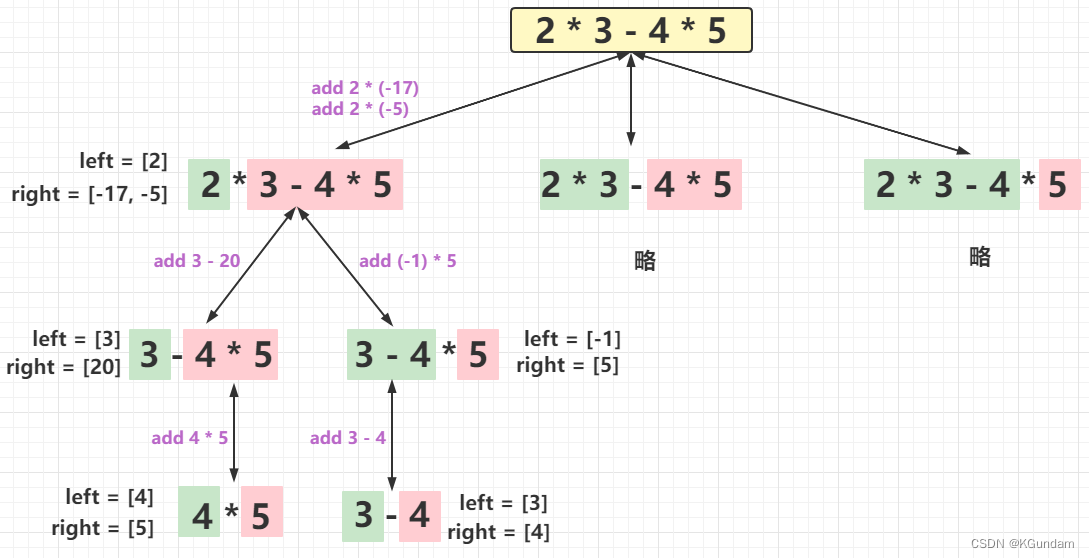
从上到下递归,结果从下到上返回,从而处理所有情况,详细代码如下:
我的代码：
class Solution
{
public:
vector<int> diffWaysToCompute(string expression)
{
vector<int> ways; //存所有结果
// 对于输入表达式的每一个字符
for (int i = 0; i < expression.length(); ++i)
{
char c = expression[i];
//判断是否是运算符
if (c == '+' || c == '-' || c == '*')
{
//利用递归的形式分开提取所有可能的左右结果子集(分治处理)
vector<int> left = diffWaysToCompute(expression.substr(0, i));
vector<int> right = diffWaysToCompute(expression.substr(i + 1));
//提取完之后两两组合处理(这里两两组合的l和r一定是数字,它们都被下面的一层递归处理过了)
for (const int & l : left)
{
for (const int & r : right)
{
switch (c)
{
case '+': ways.push_back(l + r); break;
case '-': ways.push_back(l - r); break;
case '*': ways.push_back(l * r); break;
}
}
}
}
}
//特殊情况(只有数字,所以ways未填充为空)
if (ways.empty()) ways.push_back(stoi(expression));
return ways;
}
};
还有另外一种从下到上动态规划的方法,可以减少重复的计算,但是没有分治法好理解:
/*
dp[i][j]的含义: 表达式从i到j的所有组合结果答案
*/
class Solution
{
public:
vector<int> diffWaysToCompute(string expression)
{
vector<int> data; //数字
vector<int> ops; //运算符
int num = 0;
char op = ' ';
istringstream ss(expression + "+"); //注意处理一下末尾(添加一个"+")
while (ss >> num && ss >> op) //一一对应读入num op num op num op ... (这也正是上面要加个"+"的原因)
{
//一一对应存入数组中
data.push_back(num);
ops.push_back(op);
}
int n = data.size();
vector<vector<vector<int>>> dp(n, vector<vector<int>>(n, vector<int>())); //三维数组
//这里循环遍历的是大小为n的data
//处理每个data为结尾的子情况直到更新完所有
for (int i = 0; i < n; ++i)
{
//这里采用从后往前(以i i-1 i-2 ...0开头)递推状态方程
for (int j = i; j >= 0; --j)
{
if (i == j) //内层循环首次循环时i==j我们将这个num直接存入dp[j][i](其实也就是处理dp[i][i])
{
dp[j][i].push_back(data[i]);
}
else
{
//外两层循环确定了两个数据区间[j,i] 这里确定的是中间运算符的位置(从j到i逐个处理)
for (int k = j; k < i; k += 1)
{
//这里类似分治法,分别讨论k左右的结果情况,然后进行计算
for (auto left : dp[j][k])
{
for (auto right : dp[k+1][i])
{
int val = 0;
switch (ops[k])
{
case '+': val = left + right; break;
case '-': val = left - right; break;
case '*': val = left * right; break;
}
dp[j][i].push_back(val); //将计算结果记录
}
}
}
}
}
}
return dp[0][n-1];
}
};
涉及知识点:
1.分治法
顾名思义，分治问题由“分”（divide）和“治”（conquer）两部分组成，通过把原问题分为子问题，再将子问题进行处理合并，从而实现对原问题的求解。例如归并排序就是典型的分治问题，其中“分”即为把大数组平均分成两个小数组，通过递归实现，最终我们会得到多个长度为 1 的子数组;“治”即为把已经排好序的两个小数组合成为一个排好序的大数组，从长度为 1 的子数组开始，最终合成一个大数组。
