leetcode-528.按权重随机选择
数学问题-随机与取样
题目详情
给你一个 下标从 0 开始 的正整数数组 w ,其中 w[i] 代表第 i 个下标的权重。
请你实现一个函数 pickIndex ,它可以 随机地 从范围 [0, w.length - 1] 内(含 0 和 w.length - 1)选出并返回一个下标。选取下标 i 的 概率 为 w[i] / sum(w) 。
例如,对于 w = [1, 3],挑选下标 0 的概率为 1 / (1 + 3) = 0.25 (即,25%),而选取下标 1 的概率为 3 / (1 + 3) = 0.75(即,75%)。
示例1:
输入:
["Solution","pickIndex"]
[[[1]],[]]
输出:
[null,0]
解释:
Solution solution = new Solution([1]);
solution.pickIndex(); // 返回 0,因为数组中只有一个元素,所以唯一的选择是返回下标 0。
示例2:
输入:
["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"]
[[[1,3]],[],[],[],[],[]]
输出:
[null,1,1,1,1,0]
解释:
Solution solution = new Solution([1, 3]);
solution.pickIndex(); // 返回 1,返回下标 1,返回该下标概率为 3/4 。
solution.pickIndex(); // 返回 1
solution.pickIndex(); // 返回 1
solution.pickIndex(); // 返回 1
solution.pickIndex(); // 返回 0,返回下标 0,返回该下标概率为 1/4 。
由于这是一个随机问题,允许多个答案,因此下列输出都可以被认为是正确的:
[null,1,1,1,1,0]
[null,1,1,1,1,1]
[null,1,1,1,0,0]
[null,1,1,1,0,1]
[null,1,0,1,0,0]
......
诸若此类。
思路:
先使用 partial_sum 求前缀和(即到每个位置为止之前所有数字的和)
每当需要采样时,我们可以先随机产生一个数字,然后使用二分法
查找其在前缀和中的位置,以模拟加权采样的过程。
这里借鉴力扣题解中的一个例子解释:
假设我们有数组w: [1, 2, 3, 4], 那么这个数组的的和为 1 + 2 + 3 + 4 = 10. 对应的我们得到 index {0,1,2,3} 的概率为 {1/10, 2/10, 3/10, 4/10}。现在我们要返回 {0,1,2,3} 中的随意一个index,但是我们要保证pickIndex()函数所得到这个index的概率是根据以上的权重来的。
我们把每个数(即权重)拆为1等分
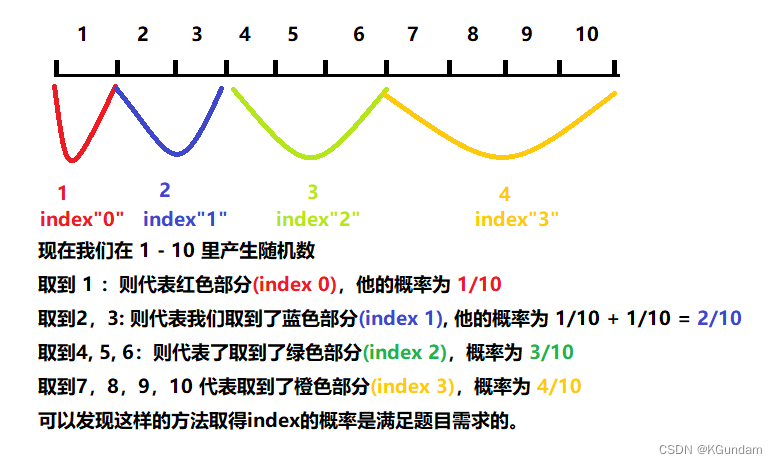
我的代码:
class Solution
{
vector<int> sums;
public:
Solution(vector<int>& w)
{
//sums存储对应下标的前缀和
//如sums[0] = w[0] sums[1] = sums[0] + w[1] ....
partial_sum(w.begin(), w.end(), back_inserter(sums));
}
/*等价于
sums.push_back(W[0]);
for(int i = 1; i < w.size(); ++i)
sums.push_back(sums.back() + w[i]);
*/
int pickIndex()
{
int pos = (rand() % sums.back()) + 1; //产生0~sums.back()之间的随机数
//二分法查找pos在sums区间里的位置,减去begin的差值即为pos的下标即为所求
return lower_bound(sums.begin(), sums.end(), pos) - sums.begin();
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* obj = new Solution(w);
* int param_1 = obj->pickIndex();
*/





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 全程不用写代码,我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 记一次.NET内存居高不下排查解决与启示
· DeepSeek 开源周回顾「GitHub 热点速览」
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了