leetcode-218.天际线问题

---

题目详情

简单的概括一下题目:给定建筑物的起止位置和高度，返回建筑物轮廓（天际线）的拐点。

---

示例1：

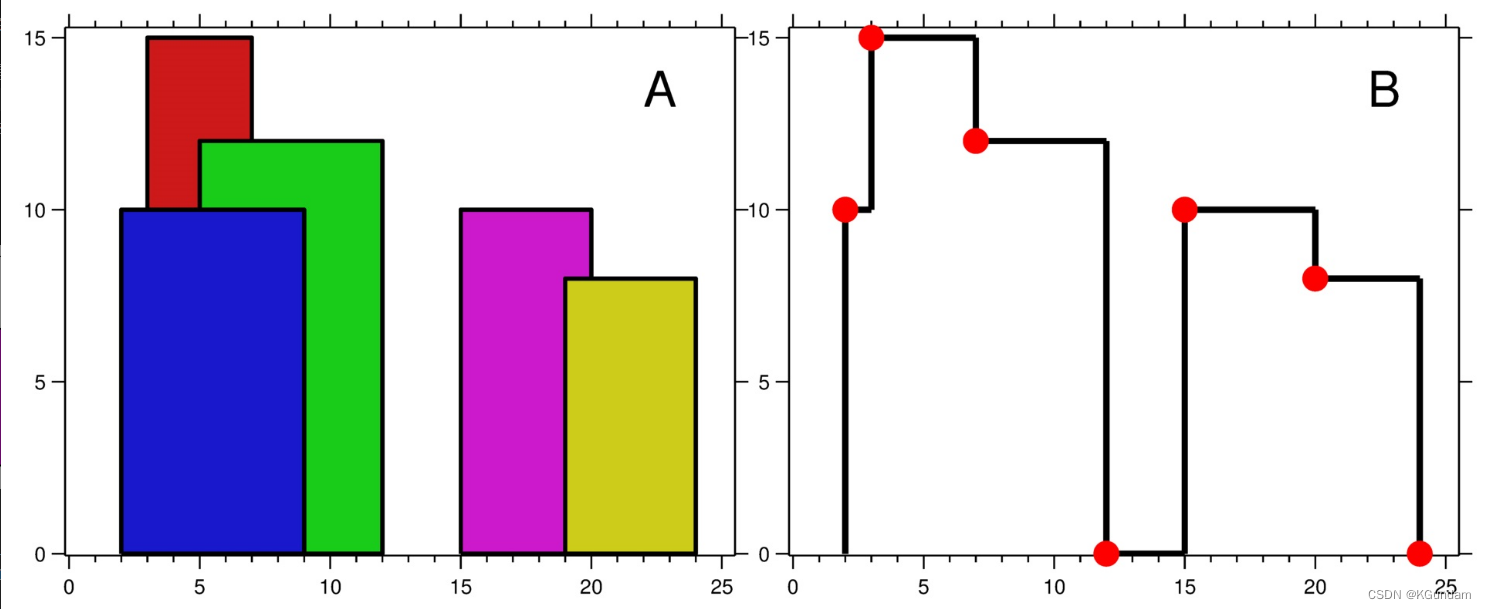
输入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释：
图 A 显示输入的所有建筑物的位置和高度，
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。

示例2:

输入：buildings = [[0,2,3],[2,5,3]]
输出：[[0,3],[5,0]]

首先,这道题要求我们寻找一些关键点,这些关键点一定位于高度变化的地方
所以我们需要用一个数据结构记录从左到右扫过的高度的变化情况,要实现:
1.当我们遇到一个大楼的左端点时,将这个大楼的高度加入记录
2.当我们遇到一个大楼的右端点时,将这个大楼的高度删除记录
要想实现2,必须要能查找到对应的高度进行删除
set只能存储一些互不相同的元素,而这道题可能会产生相同高度的情况
所以我们就利用允许有相同元素的multiset数据结构

详细代码及解释：

class Solution 
{
public:
    vector<vector<int>> getSkyline(vector<vector<int>>& buildings) 
    {
        vector<vector<int>> res;
        vector<pair<int, int>> height;
        for (auto &b : buildings)//记录每个建筑的左右端点,高度
        {
        /*
        b[0],b[1]是建筑左、右端点 b[2]是建筑的高度
        但是为什么记录高度b[2]时要一个负一个正呢?
        因为我们下面有一个sort操作,而sort会从小到大排序
        height从小到大排序,b[0],b[1]这些端点可能会存在重合情况
        当左端点重合时,我们要的是最高点,因为此时总天际线是拔高的
        当右端点重合时,我们要的是最低点,因为此时总天际线是降低的
        只要我们将左端点对应的高度设置为相反数,那么sort将会实现:
        左端点重合就按照高度从高到低排序,右端点重合就按照从低到高排序
        */  
            height.push_back({b[0], -b[2]});
            height.push_back({b[1], b[2]});
        }
        sort(height.begin(), height.end()); //排序后遍历的将是一个个端点而不是一个个建筑

        multiset<int> st;
        st.insert(0);   //我们最终天际线肯定是归为平地0的,这里需要初始化一下
        //之前的最大高度       当前的最大高度
        int preMaxHeight = 0, curMaxHeight = 0;
        for (auto &h : height) //遍历排好序的端点
        {
            //h.second<0说明是某个左端点(有重合情况的时候这里就会是较高的)
            if (h.second < 0) //"可能"需要拔高天际线了("可能"的原因:可能不高于当前最高建筑)
            {
                st.insert(-h.second); //高度取回正数入队(入队后自动由高到低排序好了)
            }
            else      //右端点 "可能"需要降低天际线了("可能"的原因:可能不是当前最高建筑的右端点)
            {
                st.erase(st.find(h.second));//当前右端点对应的高度出队(对应建筑结束了)
            }

            curMaxHeight = *st.rbegin();//临时存储当前的最大高度

            if (curMaxHeight != preMaxHeight) //最大高度变化了,就需要存入这个关键点了
            {
                res.push_back({h.first, curMaxHeight});//存入当前关键点
                preMaxHeight = curMaxHeight;          //当前最高赋予上一次最高
            }
        }
        return res;
    }
};