经典算法题目-动态规划
动态规划
动归五部曲
一、确定dp数组以及下标的含义
二、确定递推公式
三、dp数组进行初始化
四、确定遍历顺序
五、举例推导dp数组
746. 使用最小花费爬楼梯
-
解决思路
- 定义dp[i] 为爬到第i个台阶的最低花费
- 递推公式。因为每一次能爬一步或两步,dp[i] 为前面的两格走两步过来或走一步过来
- 遍历顺序。i从小到大即可
-
代码
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length+1];
for(int i = 2; i < cost.length+1; i++){
dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[cost.length];
}
背包问题
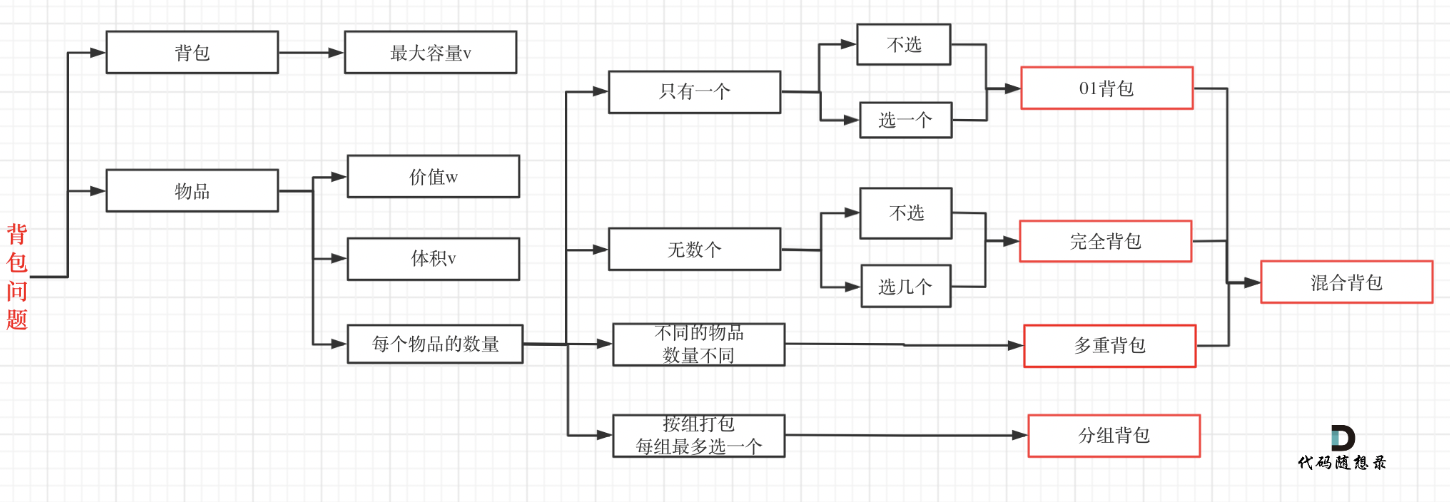
01背包
问题
- n个物品、背包重量w,i物件重量weight[i],价值value[i],每件物品只能用一次。求能放哪些物品价值总和最大
一维dp解决思路
-
定义dp数组。dp[j] 容量为j的背包能放物品的最大值
-
递推公式。
- dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
- 比较放入当前物品的价值、和不放当前物品 (此时dp[j] 为不放i物品容量为w的最大价值)
-
初始化。dp[0] = 0
-
遍历顺序
- 如果采用二维数组,根据递推公司,是右下角由左上角的元素计算得来
- 而采用一维数组滚动存储二维的数据,遍历顺序物品类型从小到大,背包重量维度从大到小
- 当背包重量维度从小到大遍历时,代表着背包里可以放多个相同的物品
代码
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
int wLen = weight.length;
//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值
int[] dp = new int[bagWeight + 1];
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 0; i < wLen; i++){
for (int j = bagWeight; j >= weight[i]; j--){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
}
企鹅号:1272420336,一起学习,一起进步~




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 三行代码完成国际化适配,妙~啊~
· .NET Core 中如何实现缓存的预热?