LeetCode图专题(未完成)
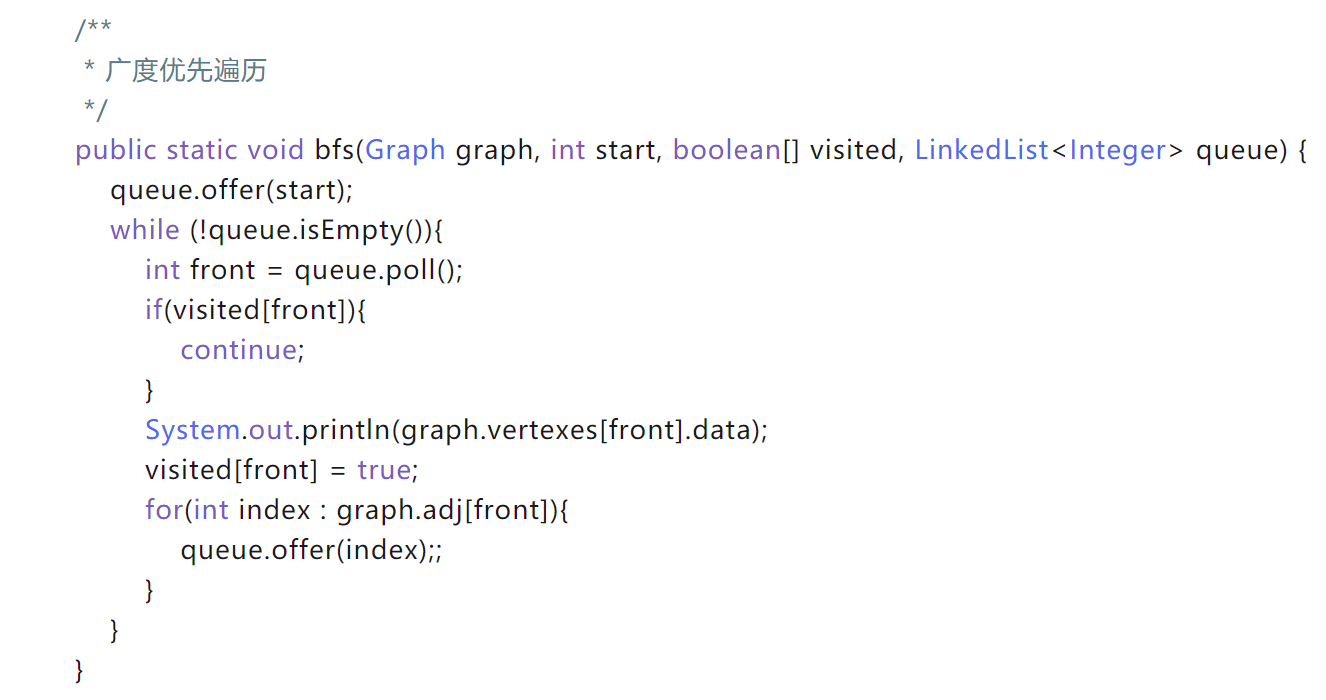
图可以用邻接矩阵(顶点和顶点矩阵)和邻接表(顶点的链表)两种形式的结构来存储。
还有逆邻接表,顶点依然是头结点,但后续存的是谁指向你的。还有十字链表。。。
图的遍历:DFS,BFS 搞搞清楚
DFS就是遍历头结点的邻节点们,假如这个邻节点没有被访问过,就递归调用dfs。

除了递归还能用栈后进先出,做while循环判断栈是否为空,在循环内先poll再add邻节点们??不对啊应该只add一个啊(需要一条路走下去)?(没看到用栈的代码。。。)
深度优先搜索是递归过程,带有回退操作,因此需要使用栈存储访问的路径信息。当访问到的当前顶点没有可以前进的邻接顶点时,需要进行出栈操作,将当前位置回退至出栈元素位置。(这意思是递归+栈。。。这个栈接收回退在上面代码中是被visited取代了吗?我晕了。。能不能给给代码。。。(补:210的方法2,又有dfs递归又有栈stack又有状态visied....)
BFS用队列前面出后面入,先进先出。做while循环判断队列是否为空,在循环内先poll再add邻节点们,是先add的先出来,顺序和add时一致。
二分图
如果可以用两种颜色对图中的节点进行着色,并且保证相邻的节点颜色不同,那么这个图就是二分图。
1. 判断是否为二分图
785. Is Graph Bipartite? (Medium)
如果我们能将一个图的节点集合分割成两个独立的子集A和B,并使图中的每一条边的两个节点一个来自A集合,一个来自B集合,我们就将这个图称为二分图。
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation:
The graph looks like this:
0----1
| |
| |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.
emmmm差点没看懂这多维数组是如何表示图。。。省略了顶点。
任何两点都走得通的图是连通图,否则是非连通图。
答案:深度优先搜索着色【通过】
思路:
如果节点属于第一个集合,将其着为蓝色,否则着为红色。只有在二分图的情况下,可以使用贪心思想给图着色:一个节点为蓝色,说明它的所有邻接点为红色,它的邻接点的所有邻接点为蓝色,依此类推。
算法:
使用数组(或者哈希表)记录每个节点的颜色: color[node]。颜色可以是 0, 1,或者未着色(-1 或者 null)。
搜索节点时,需要考虑图是非连通的情况。对每个未着色节点,从该节点开始深度优先搜索着色。每个邻接点都可以通过当前节点着相反的颜色。如果存在当前点和邻接点颜色相同,则着色失败。
使用栈完成深度优先搜索(之前树的时候用的递归,但也记得可以用栈),栈类似于节点的 “todo list”,存储着下一个要访问节点的顺序。在 graph[node] 中,对每个未着色邻接点,着色该节点并将其放入到栈中。
时间复杂度:O(N + E),其中 N 是节点的数量,E 是边的数量。着色每个节点时,遍历其所有边(比如有3个邻节点是找3条边)。
空间复杂度:O(N),存储 color 的栈。
-------------------------------------------------------------------------------------------------------
graph将会以邻接表方式给出,graph[i]表示图中与节点 i 相连的所有节点。每个节点都是一个在0到graph.length-1之间的整数(?顶点数?)。这图中没有自环和平行边: graph[i] 中不存在 i,并且graph[i]中没有重复的值。
class Solution { public boolean isBipartite(int[][] graph) { int n = graph.length;//这个是顶点数 行数 就是大一维数组里面的元素个数 int[] color = new int[n];//定义一个记录顶点颜色的数组 Arrays.fill(color, -1);//初始化都未上色 for (int start = 0; start < n; ++start) {//遍历顶点们 ++i和i++在没赋值的情况下都一样吧?都是i自增啊? if (color[start] == -1) { //这是一个大的判断,不满足直接回到for的下一个 Stack<Integer> stack = new Stack();//下一个没上色的进新栈 stack.push(start);//如果该节点未上色,则进一个新栈 color[start] = 0;//给它上0色 while (!stack.empty()) {//这里循环好久 从0的邻节点们 到邻节点的邻节点们
直到邻节点们都已经上色且不冲突,全部出栈了才结束while 进去出来的过程还真是前序遍历 Integer node = stack.pop();//所以这里不只是i 需要定义一个node变量 for (int nei: graph[node]) {//遍历该上完色弹出的顶点的相邻点们 这不是dfs了吧?dfs是一条路走下去不管全部的啊,这像bfs?
if (color[nei] == -1) { stack.push(nei);//没上色的邻节点又进栈 所以while不能是if 虽然前面只有1个进来又出去 但这里可能有多个进栈 color[nei] = color[node] ^ 1;// ^按位异或 } else if (color[nei] == color[node]) {//如果与邻节点颜色相同 false return false; } } } } } return true; } } 作者:LeetCode 链接:https://leetcode-cn.com/problems/is-graph-bipartite/solution/pan-duan-er-fen-tu-by-leetcode/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
放入栈中代表着下一步要对他着色了。todo他。
要想实现回溯,可以利用栈的先入后出特性,也可以采用递归的方式(因为递归本身就是基于方法调用栈来实现)。
DFS的栈实现,我感觉这一题就是:先入栈一个顶点,然后又出栈该节点,入栈它的邻节点们。栈不为空的循环下,再出栈刚放进去的邻节点的最后一个,入栈该邻节点的邻节点们。。。推下去直到没有邻节点了,此时循环依然需要出栈,则开始回溯,再发展,没有的话再回溯,没有的话再回溯,直到栈为空。
但是漫画里最先入栈的那些不需要出栈,最后没有邻节点的才开始回溯。这儿答案可能为了简写代码就一条出栈语句?还有条件不一样那儿是找没访问过的,这儿需要把邻节点染不同颜色。
--------------------------------------------------------------------------------------------------
这没有用到stack看起来还简单一些 但实际用的相反色递归好难理解。。。
public boolean isBipartite(int[][] graph) { int[] colors = new int[graph.length]; Arrays.fill(colors, -1);
for (int i = 0; i < graph.length; i++) { // 处理图不是连通的情况 这里也是遍历节点 if (colors[i] == -1 && !isBipartite(i, 0, colors, graph)) { return false; } } return true;//情况就是遍历的顶点们不是上面的情况(未着色且方法返回false)就是true } private boolean isBipartite(int curNode, int curColor, int[] colors, int[][] graph) {//重载判断是不是二分图 因为需要的判断参数多一些 if (colors[curNode] != -1) { return colors[curNode] == curColor;//若遍历的该节点已经上色,则返回判断该节点的颜色是否是0 } colors[curNode] = curColor;//没有上色的话给他上0色 for (int nextNode : graph[curNode]) {//遍历他的邻节点们 判断递归方法的结果(传入的是相反色,若方法返回true的话就是true) if (!isBipartite(nextNode, 1 - curColor, colors, graph)) {//若递归方法返回false的话这里也是false return false; } } return true; }
拓扑排序
常用于在具有先序关系的任务规划中。
有向无环图(Directed Acyclic Graph, DAG)是有向图的一种,字面意思的理解就是图中没有环(没有自己指向自己,和来回指向形成环的(2个节点3个节点及以上都有可能))。常常被用来表示事件之间的驱动依赖关系,管理任务之间的调度。
AOV网:在每一个工程中,可以将工程分为若干个子工程,这些子工程称为活动。如果用图中的顶点表示活动,以有向图的弧表示活动之间的优先关系,这样的有向图称为AOV网,即顶点表示活动的网。在AOV网中,如果从顶点vi到顶点j之间存在一条路径,则顶点vi是顶点vj的前驱,顶点vj是顶点vi的后继。活动中的制约关系可以通过AOV网中的表示。 在AOV网中,不允许出现环,如果出现环就表示某个活动是自己的先决条件。因此需要对AOV网判断是否存在环,可以利用有向图的拓扑排序进行判断。
拓扑序列:设G=(V,E)是一个具有n个顶点的有向图,V中的顶点序列v1,v2,…,vn,满足若从顶点vi到vj有一条路径,则在顶点序列中顶点vi必在vj之前,则我们称这样的顶点序列为一个拓扑序列。
拓扑排序:拓扑排序是对一个有向图构造拓扑序列的过程。有两个方法,一是入度表法(看入度),二是DFS(看出度)。【详见链接】
拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
(1)每个顶点出现且只出现一次。
(2)若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
注:有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说
1. 课程安排的合法性
207. Course Schedule (Medium)
你这个学期必须选修 numCourse 门课程,记为 0 到 numCourse-1 。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1]
给定课程总量以及它们的先决条件,请你判断是否可能完成所有课程的学习?
2, [[1,0]]
return true
emmmm答案见评论区
核心思想就是:
先构造邻接表和节点入度数组,用队列记录初始的入度为0的节点,从队列中取元素,将该节点指向的那些节点的入度-1(删除操作),若有新的入度为0的节点,加入队列中,直到队列为空,排序结束,判断取出来的节点的数目是否==图节点数目,否则有环
class Solution { public boolean canFinish(int numCourses, int[][] prerequisites) {//numCourses个结点的有向图 后面只是个二维数组 int n=prerequisites.length;//n条边 好吧是边 不过上一题规定了边表数量一样 这里没啥用啊也 用的都是顶点数 可删除这行代码
//想起来了二维数组之前学的矩阵的length就是行数啊啊啊啊,这里就是元素个数,邻接表里就是顶点个数啊 ArrayList<Integer> [] adjacencyList=new ArrayList[numCourses];//邻接表 是arraylist类型的数组 也就是说每个元素是一个list集合 int [] inDegree=new int[numCourses];//入度数组,inDegree[i]的值表示节点i的入度 //构建邻接表 for(int i=0;i<numCourses;i++){//adj有节点个元素 adjacencyList[i]=new ArrayList<>();//节点i的下标为i 还需要具体给每个元素分配list空间?可能就得有<>() } for (int [] pre:prerequisites) {//取行,就是取它给的二维数组中每一个行元素。比如【0,1】想修0必先修1
//是在把题目中给的弄到邻接表里去。这次给的多维数组不是邻接表还反了 adjacencyList[pre[1]].add(pre[0]);//比如pre=[0,1],1是边的起始点,0才是终点,是节点1指向节点0 哦哦这是题目要求
//所以这里是后面的课为头节点 即邻接表数组的索引(用矩阵看就是该行数) 前面那个为头节点的指向,加到该索引指向的list里面 inDegree[pre[0]]++//拓扑排序判断是不是DAG return topologicalSort(adjacencyList,inDegree,numCourses); } private boolean topologicalSort(ArrayList<Integer> [] adjacencyList,int [] inDegree,int n){//邻接表和入度数组 int res=0;//拓扑排序能取出来的节点数目 Queue<Integer> queue=new LinkedList<Integer>();//存储入度为0的节点 for(int i=0;i<n;i++){ if(inDegree[i]==0) queue.offer(i);//节点i的入度为0,添加进队列 } while (!queue.isEmpty()) { //这里又有点DFS的意思了 想起做的栈和队列的题 好像都是这样循环 难道都是DFS?等一下答案说是BFS?。。。 int i = queue.poll();//取出节点i 也是和上一题一样循环一进来就先出。。。但这个是队列上一题是栈 res++;//出一个加一个 for (int child_of_i : adjacencyList[i]) {//对节点i指向的每一个节点 inDegree[child_of_i]--;//入度-1 if (inDegree[child_of_i] == 0) queue.offer(child_of_i); } } return res==n; } } 作者:jin-ai-yi 链接:https://leetcode-cn.com/problems/course-schedule/solution/tuo-bu-pai-xu-de-ban-fa-pan-duan-you-xiang-tu-shi-/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
我的老天鹅...IT'S TOO HARD FOR ME...
复习一下:
class Solution { public boolean canFinish(int numCourses, int[][] prerequisites) { ArrayList<Integer>[] adj = new ArrayList[numCourses]; int[] inDegree = new int[numCourses]; for(int i = 0;i<numCourses;i++){ adj[i] = new ArrayList<>(); } for(int[] pre:prerequisites){ adj[pre[1]].add(pre[0]);//课程只有先修谁后修谁这2个 索引0和索引1 inDegree[pre[0]]++; } return topLogicalSort(adj,inDegree,numCourses); } public boolean topLogicalSort(ArrayList<Integer>[] adj,int[] inDegree,int n){ int res = 0; Queue<Integer> queue = new LinkedList<>(); for(int i = 0;i<inDegree.length;i++){ if(inDegree[i]==0){ queue.add(i); } } while(!queue.isEmpty()){ int i = queue.poll(); res++; for(int child_of_i:adj[i]){ inDegree[child_of_i]--; if(inDegree[child_of_i]==0){ queue.add(child_of_i); } } } return res==n; } }
还有dfs也可以解决此题,不过要变通一下,一个节点的状态不再是访问过/没访问过两种,而是:
0:当前节点尚未访问过;1:当前节点在其他轮的dfs中被访问过了;2:当前节点在本轮dfs中被访问过了,有环
因为主循环里每一次dfs的时候,只有访问到本轮dfs的过程中访问过的节点,才说明这个dfs得到的路径是个环;若是访问到其他轮dfs中访问过的节点,与本轮dfs无关,不应考虑
只有在“访问到本轮dfs的过程中的重复节点”,才说明是环
class Solution { public boolean canFinish(int numCourses, int[][] prerequisites) { //先构造邻接矩阵 int [][] AdjacencyMatrix=new int[numCourses][numCourses]; int [] visited=new int[numCourses];//访问情况记录,dfs的时候,0:尚未访问过;
//1:在其他节点为起始的时候访问过了; 2:在当前节点起始的时候访问过了,有环,直接返回false for (int[] pre:prerequisites) { AdjacencyMatrix[pre[1]][pre[0]]=1;//pre[1]指向pre[0]的一条边 邻接矩阵元素Aij为1时是i指向j } for(int i=0;i<numCourses;i++){//对节点i if(visited[i]==0) { if (!dfs(AdjacencyMatrix, visited, i)) return false; } } return true; } private boolean dfs(int [][] AdjacencyMatrix,int [] visited,int i){ if(visited[i]==2) return false;//在主循环的一轮dfs中访问了同一个节点两次,有回路 我明白了 这里主要是供下面那个dfs用的 visited[i]=2; for(int j=0;j<AdjacencyMatrix.length;j++){//邻接矩阵行遍历 if(AdjacencyMatrix[i][j]==1){ if(dfs(AdjacencyMatrix,visited,j)==false) return false; } } visited[i]=1;//从节点i开始的dfs结束,下一次 return true; } }
好难理解啊。。。没太懂。。。
2. 课程安排的顺序
210. Course Schedule II (Medium)
4, [[1,0],[2,0],[3,1],[3,2]]
There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2.
Both courses 1 and 2 should be taken after you finished course 0. So one correct course order is [0,1,2,3].
Another correct ordering is[0,2,1,3].
我是根据上一题用队列做的拓扑排序。用队列好像就是BFS不是DFS
class Solution { public int[] findOrder(int numCourses, int[][] prerequisites) { ArrayList<Integer>[] adj = new ArrayList[numCourses]; int[] inDegree = new int[numCourses]; for(int i = 0;i<numCourses;i++){ adj[i] = new ArrayList<>();//这是给每一个元素存一个list空间 } for(int[] pre:prerequisites){ adj[pre[1]].add(pre[0]); inDegree[pre[0]]++; } ArrayList<Integer> list = new ArrayList<>(); list if(list==null){ return new int[0];//返回一个空数组要这样写 } int[] array = new int[list.size()];//ilst转array要这样写 for(int i = 0; i < list.size();i++){ array[i] = list.get(i); } return array; } public ArrayList<Integer> topLogicSort(ArrayList<Integer>[] adj,int[] inDegree,int n){ ArrayList<Integer> list = new ArrayList<>(); int res=0; Queue<Integer> queue = new LinkedList<>(); for(int i = 0;i<n;i++){ if(inDegree[i]==0){ queue.add(i); } } while(!queue.isEmpty()){ int i = queue.poll(); list.add(i); res++; for(int child_of_i:adj[i]){ inDegree[child_of_i]if(inDegree[child_of_i]==0){ queue.add(child_of_i); } } } if(res==n){ return list; } return null; } }
看答案整理一下:
BFS 的总体思路:(卧槽都没有建立邻接表吗直接拿输入的二维数组当邻接表吗??)
建立入度表,入度为 0 的节点先入队
当队列不为空,节点出队,标记学完课程数量的变量加 1,并记录该课程
将课程的邻居入度减 1
若邻居课程入度为 0,加入队列
用一个变量记录学完的课程数量,一个数组记录最终结果,简洁好理解。
DFS 的总体思路:
建立邻接矩阵
DFS 访问每一个课程,若存在环直接返回
status 保存课程的访问状态,同一个栈保存课程的访问序列。
方法 1: 最简单的 BFS(真的是把输入的参数直接当邻接表的作用使,前面都可以这样,简便好多)
// 方法 1 最简单的 BFS public int[] findOrder(int numCourses, int[][] prerequisites) { if (numCourses == 0) return new int[0]; int[] inDegrees = new int[numCourses]; // 建立入度表 for (int[] p : prerequisites) { // 对于有先修课的课程,计算有几门先修课 inDegrees[p[0]]++; } // 入度为0的节点队列 Queue<Integer> queue = new LinkedList<>(); for (int i = 0; i < inDegrees.length; i++) { if (inDegrees[i] == 0) queue.offer(i); } int count = 0; // 记录可以学完的课程数量 int[] res = new int[numCourses]; // 可以学完的课程 // 根据提供的先修课列表,删除入度为 0 的节点 while int curr = queue.poll(); res[count++] = curr; // 将可以学完的课程加入结果当中 for (int[] p : prerequisites) { if (p[1] == curr){//遍历出2个一组的元素们 要是该组后面这个也就是头结点出队列了的话 前面这个入度就减去1 inDegrees[p[0]]--; if (inDegrees[p[0]] == 0) queue.offer(p[0if (count == numCourses) return res; return new int[0]; } 作者:kelly2018 链接:https://leetcode-cn.com/problems/course-schedule-ii/solution/java-jian-dan-hao-li-jie-de-tuo-bu-pai-xu-by-kelly/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
方法 2:邻接矩阵(数组) + DFS (上一题第2解有点类似,但是我没太懂)
// 方法 2:邻接矩阵 + DFS 由于用的数组,每次都要遍历,效率比较低 public int[] findOrder(int numCourses, int[][] prerequisites) { if (numCourses == 0) return new int[0]; // 建立邻接矩阵 // 记录访问状态的数组,访问过了标记 -1,正在访问标记 1,还未访问标记 0 int[] status = new int[numCourses]; Stack<Integer> stack = new Stack<>(); // 用栈保存访问序列
for (int i = 0; i < numCourses; i++) { if (!dfs(graph, status, i, stack)) return new int[0]; // 只要存在环就返回 }
int[] res = new int[numCourses]; for (int i = 0; i < numCourses; i++) { res[i] = stack.pop(); } return res; } private boolean dfs(int[][] graph, int[] status, int i, Stack<Integer> stack) { if (status[i] == 1) return false; // 当前节点在此次 dfs 中正在访问,说明存在环 主要是供下面那个递归dfs用的,一条龙判断递归走下去 if (status[i] == -1) return true; //被别的一条龙访问过 status[i] = 1; for (int j = 0; j < graph.length; j++// dfs 访问当前课程的后续课程,看是否存在环 if (graph[i][j] == 1 && !dfs(graph, status, j, stack)) return false; } status[i] = -1; // 标记为已访问 stack.push(i); return true; } 作者:kelly2018 链接:https://leetcode-cn.com/problems/course-schedule-ii/solution/java-jian-dan-hao-li-jie-de-tuo-bu-pai-xu-by-kelly/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
需要复习。。。跟上一个dfs一样。。还有这里不用对栈逆序?为啥其他的需要?
并查集
并查集可以动态地连通两个点,并且可以非常快速地判断两个点是否连通。
1. 冗余连接
684. Redundant Connection (Medium)
在本问题中, 树指的是一个连通且无环的无向图。
输入一个图,该图由一个有着N个节点 (节点值不重复1, 2, ..., N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ,满足 u < v,表示连接顶点u 和v的无向图的边。
返回一条可以删去的边,使得结果图是一个有着N个节点的树。如果有多个答案,则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式 u < v。
示例 1:
输入: [[1,2], [1,3], [2,3]]
输出: [2,3]
解释: 给定的无向图为:
1
/ \
2 - 3
题目描述:有一系列的边连成的图,找出一条边,移除它之后该图能够成为一棵树。
答案:
没看懂。。。先跳了。。。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号